Chào mừng bạn đến với bài học về lý thuyết phép nhân số nguyên trong chương trình Toán 6 KNTT. Bài học này sẽ giúp bạn hiểu rõ về quy tắc nhân hai số nguyên, cách áp dụng vào giải các bài toán thực tế và kết nối kiến thức với cuộc sống hàng ngày.
Chúng ta sẽ cùng nhau khám phá các khái niệm cơ bản, ví dụ minh họa và bài tập vận dụng để nắm vững kiến thức này một cách hiệu quả nhất.
Lý thuyết Phép nhân số nguyên Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu
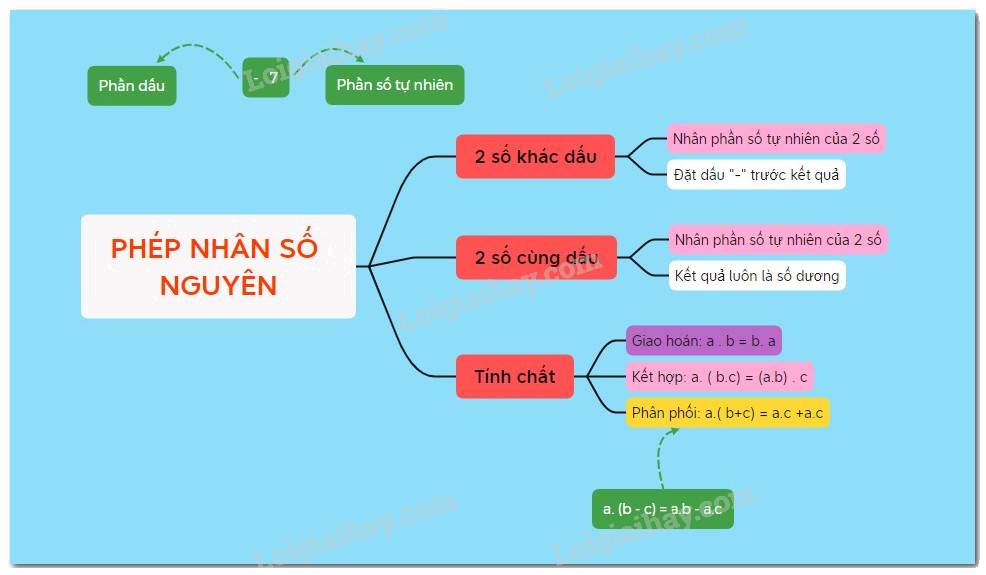
1. Quy tắc nhân hai số nguyên khác dấu
Muốn nhân hai số nguyên khác dấu, ta nhân phần số tự nhiên của chúng rồi đặt dấu “-” trước kết quả nhận được.
Ví dụ:
\(5.( - 5) = - 25\)
\(\begin{array}{l}\left( { - 5} \right).9 = - \left( {5.9} \right) = - 45\\3.\left( { - 3} \right) = - \left( {3.3} \right) = - 9\\\left( { - 6} \right).0 = 0\end{array}\)
Chú ý:
+) \(a.0 = 0\)
+) Cách nhận biết dấu của tích:
\(\left( + \right).\left( + \right)\) \( \to \left( + \right)\)
\(\left( - \right).\left( - \right) \to \left( + \right)\)
\(\left( + \right).\left( - \right) \to \left( - \right)\)
\(\left( - \right).\left( + \right) \to \left( - \right)\)
+) \(a.b = 0\) thì \(a = 0\) hoặc \(b = 0\)
+) Khi đổi dấu một thừa số thì tích đổi dấu. Khi đổi dấu hai thừa số thì tích không thay đổi.
+) \(\left( { - a} \right).a = a.\left( { - a} \right) = - {a^2}\)
2.Quy tắc nhân hai số nguyên cùng dấu
Muốn nhân hai số nguyên cùng dấu, ta nhân phần số tự nhiên của chúng rồi đặt dấu “+” trước kết quả của chúng.
Ví dụ: \(( - 5).\left( { - 6} \right) = 5.6 = 30\)
+ Nhân hai số nguyên dương nghĩa là nhân hai số tự nhiên khác \(0.\)
+ Nhân hai số nguyên âm ta nhân phần số tự nhiên của chúng.
Nhận xét: Tích của hai số nguyên âm là một số nguyên dương
Chú ý:
+) \(a.0 = 0.a = 0\)
+) \(a.b = 0\) thì \(a = 0\) hoặc \(b = 0.\)
3.Tính chất của phép nhân
Giao hoán: \(a.b = b.a\)
Kết hợp: \(\left( {a.b} \right).c = a.\left( {b.c} \right)\)
Nhân với số \(1:\) \(a.1 = 1.a = a\)
Tính chất phân phối của phép nhân đối với phép cộng: \(a.\left( {b + c} \right) = ab + ac\)
Tính chất trên cũng đúng đối với phép trừ: \(a\left( {b - c} \right) = ab - ac\)
Ví dụ:
Thực hiện phép tính:
a) \(\left( { - 12} \right).3.\left( { - 5} \right)\)
\(\begin{array}{l}\left( { - 12} \right).3.\left( { - 5} \right) = \left( { - 12} \right).\left( { - 5} \right).3\\ = \left[ {\left( { - 12} \right).\left( { - 5} \right)} \right].3 = \left( {12.5} \right).3\\ = 60.3 = 180\end{array}\)
b) \(\left( { - 3} \right).\left( {100 - 2} \right)\)
\(\begin{array}{l}\left( { - 3} \right).\left( {100 - 2} \right) = \left[ {\left( { - 3} \right).100} \right] - \left[ {\left( { - 3} \right).2} \right]\\ = \left( { - 3} \right).100 - \left[ { - \left( {3.2} \right)} \right]\\ = - \left( {3.100} \right) - \left( { - 6} \right)\\ = - 300 + 6 = - \left( {300 - 6} \right) = - 294\end{array}\)
Chú ý:
+ Nhờ tính chất kết hợp ta có tích của ba, bốn, năm… số nguyên.
+ Khi thực hiện phép nhân nhiều số nguyên, ta có thể dựa vào các tính chất giao hoán và kết hợp để thay đổi vị trí giữa các thừa số, đặt dấu ngoặc để nhóm các thừa số thích hợp.
+ Tích của \(n\) số nguyên \(a\) là lũy thừa bậc \(n\) của số nguyên \(a.\)
Phép nhân số nguyên là một trong những phép toán cơ bản trong toán học, đặc biệt quan trọng ở chương trình Toán 6. Hiểu rõ lý thuyết và quy tắc của phép nhân số nguyên là nền tảng để giải quyết các bài toán phức tạp hơn trong tương lai.
Phép nhân số nguyên là phép toán thực hiện giữa hai số nguyên. Kết quả của phép nhân hai số nguyên được gọi là tích.
Để hiểu rõ hơn về phép nhân số nguyên, chúng ta cần nắm vững các quy tắc sau:
Ví dụ 1: Tính (+4) * (+5)
Áp dụng quy tắc 1, ta có: (+4) * (+5) = +20
Ví dụ 2: Tính (-3) * (+2)
Áp dụng quy tắc 2, ta có: (-3) * (+2) = -6
Ví dụ 3: Tính (-1) * (-7)
Áp dụng quy tắc 1, ta có: (-1) * (-7) = +7
Phép nhân số nguyên không chỉ là một khái niệm toán học trừu tượng mà còn ứng dụng rất nhiều trong cuộc sống hàng ngày. Ví dụ:
Hãy thực hành giải các bài tập sau để củng cố kiến thức về phép nhân số nguyên:
Khi thực hiện phép nhân số nguyên, bạn cần chú ý đến dấu của các số hạng. Việc xác định đúng dấu của tích là rất quan trọng để đảm bảo kết quả chính xác.
Hy vọng bài học về lý thuyết phép nhân số nguyên Toán 6 KNTT với cuộc sống này đã giúp bạn hiểu rõ hơn về phép toán quan trọng này. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng vào giải quyết các bài toán thực tế.
| Số nguyên a | Số nguyên b | Tích a * b |
|---|---|---|
| +2 | +3 | +6 |
| -2 | +3 | -6 |
| +2 | -3 | -6 |
| -2 | -3 | +6 |