Chào mừng các em học sinh đến với bài học về Lý thuyết So sánh phân số. Hỗn số dương Toán 6 KNTT. Bài học này sẽ giúp các em nắm vững kiến thức cơ bản về phân số, cách so sánh phân số và ứng dụng của hỗn số dương trong cuộc sống.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng được thiết kế trực quan, dễ hiểu, cùng với các bài tập thực hành đa dạng để các em có thể tự tin chinh phục môn Toán.
Lý thuyết So sánh phân số. Hỗn số dương Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu
Phân số dương. Hỗn số dương
1. Quy đồng mẫu số nhiều phân số
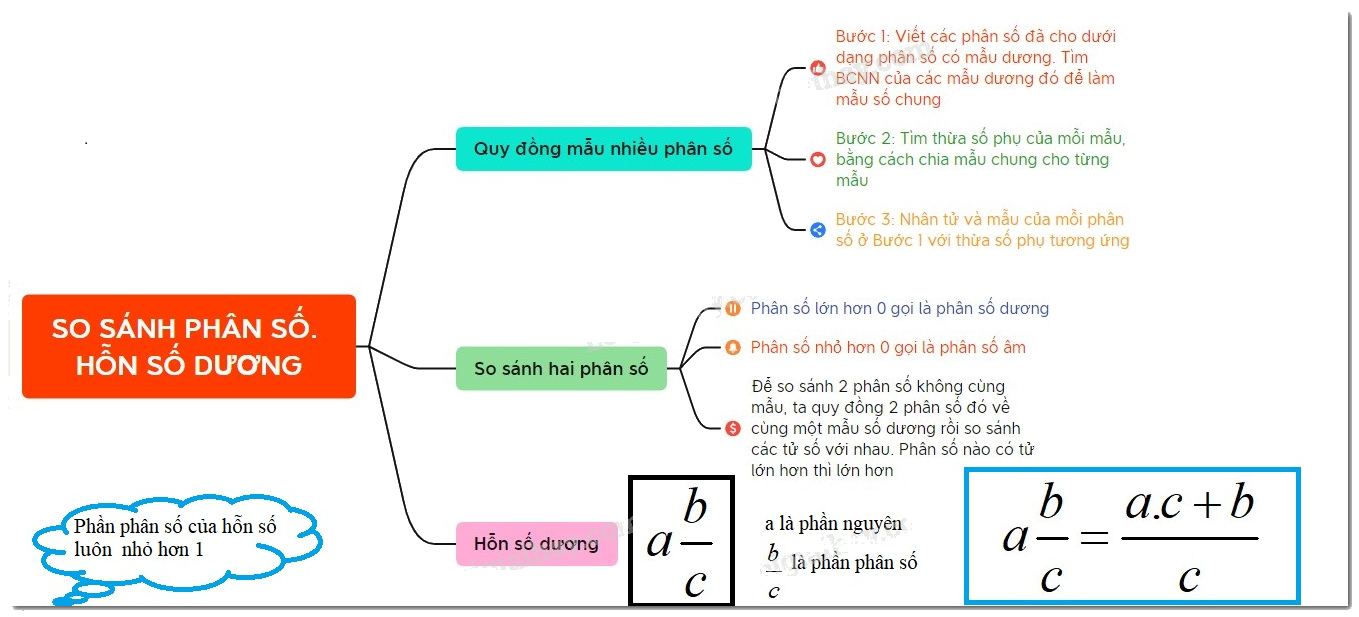
Để quy đồng nhiều phân số, ta thường làm như sau:
Bước 1: Viết các phân số đã cho dưới dạng phân số có mẫu dương. Tìm BCNN của các mẫu dương đó để làm mẫu số chung
Bước 2: Tìm thừa số phụ của mỗi mẫu, bằng cách chia mẫu chung cho từng mẫu
Bước 3: Nhân tử và mẫu của mỗi phân số ở Bước 1 với thừa số phụ tương ứng
Ví dụ:
Để quy đồng mẫu hai phân số $\dfrac{1}{6}$ và $\dfrac{3}{{ - 8}}$, ta làm như sau:
- Đưa về phân số có mẫu dương: $\dfrac{1}{6}$ và $\dfrac{{ - 3}}{8}$
- Tìm mẫu chung: $BC(6,\,8) = 24$
- Tìm thừa số phụ: $24:6 = 4;\,24:8 = 3$
- Ta có: $\dfrac{1}{6} = \dfrac{{1.4}}{{6.4}} = \dfrac{4}{{24}}$ và $\dfrac{3}{{ - 8}} = \dfrac{{ - 3}}{8} = \dfrac{{ - 3.3}}{{8.3}} = \dfrac{{ - 9}}{{24}}$.
a) Khái niệm phân số tối giản:
Phân số tối giản là phân số mà tử và mẫu chỉ có ước chung là $1$ và $ - 1$
b) Cách rút gọn phân số
Bước 1: Tìm ƯCLN của tử và mẫu khi đã bỏ dấu “-” (nếu có)
Bước 2: Chia cả tử và mẫu cho ƯCLN vừa tìm được, ta có phân số tối giản.
Ví dụ:
Để rút gọn phân số $\dfrac{{ - 15}}{{24}}$ ta làm như sau:
- Tìm ƯCLN của mẫu: ƯCLN(15, 24)=3.
- Chia cả tử và mẫu cho ƯCLN: $\dfrac{{ - 15}}{{24}} = \dfrac{{ - 15:3}}{{24:3}} = \dfrac{{ - 5}}{8}$.
Ta được $\dfrac{{ - 5}}{8}$ là phân số tối giản.
Trong hai phân số có cùng một mẫu dương, phân số nào có tử lớn hơn thì lớn hơn.
Ví dụ: So sánh $\dfrac{{ - 4}}{5}$ và $\dfrac{{ - 7}}{5}$.
Ta có: $ - 4 > - 7$ và $5 > 0$ nên $\dfrac{{ - 4}}{5} > \dfrac{{ - 7}}{5}$.
Chú ý: Với hai phân số có cùng một mẫu nguyên âm, ta đưa chúng về hai phân số có cùng mẫu nguyên dương rồi so sánh.
Ví dụ:
So sánh $\dfrac{{ - 4}}{{ - 5}}$ và $\dfrac{2}{{ - 5}}$
Đưa hai phân số trên về có cùng một mẫu nguyên âm: $\dfrac{4}{5}$ và $\dfrac{{ - 2}}{5}$
Ta có: $4 > - 2$ và $5 > 0$ nên $\dfrac{4}{5} > \dfrac{{ - 2}}{5}$.
Bước 1: Quy đồng mẫu hai phân số đã cho (về cùng một mẫu dương)
Bước 2: So sánh tử của các phân số: Phân số nào có tử lớn hơn thì lớn hơn.
Ví dụ: So sánh hai phân số $\dfrac{{ - 7}}{{12}}$ và $\dfrac{{ - 11}}{{18}}$.
$BCNN(12;18) = 36$ nên ta có:
$\dfrac{{ - 7}}{{12}} = \dfrac{{ - 7.3}}{{12.3}} = \dfrac{{ - 21}}{{36}}$
$\dfrac{{ - 11}}{{18}} = \dfrac{{ - 11.2}}{{18.2}} = \dfrac{{ - 22}}{{36}}$.
Vì $ - 21 > - 22$ nên $\dfrac{{ - 21}}{{36}} > \dfrac{{ - 22}}{{36}}$. Do đó $\dfrac{{ - 7}}{{12}} > \dfrac{{ - 11}}{{18}}$.
Cho $a$ và $b$ là hai số nguyên dương, $a > b$, $a$ không chia hết cho $b$. Nếu $a$ chia cho $b$ được thương là $q$ và số dư là $r$, thì ta viết $\dfrac{a}{b} = q\dfrac{r}{b}$ và gọi $q\dfrac{r}{b}$ là hỗn số.
Đọc là “$q,\,\,r$ phần $b$”.
Ví dụ:
Phép chia $23:4$ có thương là $5$ và số dư là $3$ nên ta có: $\dfrac{{23}}{4} = 5\dfrac{3}{4}$.
Đọc là: “ năm, ba phần tư”.
Chú ý:
Với hỗn số $q\dfrac{r}{b}$ người ta gọi $q$ là phần số nguyên và $\dfrac{r}{b}$ là phần phân số của hỗn số.
Ví dụ:
Hỗn số $5\dfrac{3}{4}$ có phần nguyên là $5$ và phần phân số là $\dfrac{3}{4}$.
Ta đổi hỗn số $q\dfrac{r}{b}$ thành phân số, theo quy tắc sau:
$q\dfrac{r}{b} = \dfrac{{q.b + r}}{b}$
Ví dụ:
$1\dfrac{3}{4} = \dfrac{{1.4 + 3}}{4} = \dfrac{7}{4}$
Trong chương trình Toán 6, việc nắm vững kiến thức về phân số là vô cùng quan trọng. Phân số xuất hiện trong rất nhiều tình huống thực tế, từ việc chia sẻ bánh kẹo đến việc đo đạc chiều dài, diện tích. Bài viết này sẽ đi sâu vào lý thuyết so sánh phân số và hỗn số dương, giúp các em học sinh hiểu rõ hơn về các khái niệm này và cách áp dụng chúng vào giải toán.
Phân số là biểu thức của một phần của một đơn vị. Một phân số được viết dưới dạng a/b, trong đó:
Ví dụ: 1/2, 3/4, 5/7 là các phân số.
Có nhiều cách để so sánh phân số:
Ví dụ: So sánh 2/3 và 3/4.
Quy đồng mẫu số: 2/3 = 8/12 và 3/4 = 9/12. Vì 8/12 < 9/12 nên 2/3 < 3/4.
Hỗn số dương là một số được viết dưới dạng tổng của một số nguyên và một phân số dương. Hỗn số dương được viết dưới dạng a b/c, trong đó:
Ví dụ: 2 1/2, 3 2/5 là các hỗn số dương.
Chuyển hỗn số dương thành phân số: a b/c = (a * c + b) / c
Chuyển phân số thành hỗn số dương: Chia tử số cho mẫu số. Phần nguyên là thương, phần phân số là số dư chia cho mẫu số.
Ví dụ:
So sánh phân số và hỗn số dương có rất nhiều ứng dụng trong cuộc sống:
Hãy thực hành giải các bài tập sau để củng cố kiến thức:
Hy vọng bài viết này đã giúp các em hiểu rõ hơn về lý thuyết so sánh phân số và hỗn số dương. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng vào giải toán một cách hiệu quả.