Chào mừng các em học sinh đến với bài học lý thuyết về tỉ số và tỉ số phần trăm trong chương trình Toán 6 Kết nối tri thức với cuộc sống. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng nhất về chủ đề này.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, các tính chất và ứng dụng thực tế của tỉ số và tỉ số phần trăm, giúp các em hiểu rõ hơn về mối liên hệ giữa các đại lượng và cách giải quyết các bài toán liên quan.
Lý thuyết Một số bài toán về tỉ số và tỉ số phần trăm Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu
a) Tỉ số của hai số
Tỉ số của hai số $ a$ và $ b$ tùy ý $ \left( {b \ne 0} \right)$ là thương của phép chia số $ a$ cho số $ b$ . Kí hiệu là $ a:b$ hoặc $ \dfrac{a}{b}$ .
Chú ý: Nếu tỉ số của $ a$ và $ b$ được viết dưới dạng $ \dfrac{a}{b}$ thì ta cũng gọi $ a$ là tử số và $ b$ là mẫu số.
Ví dụ:
Tỉ số của $ - 5$ và $ 7$ là: $ \dfrac{{ - 5}}{7}$ .
b) Tỉ số của hai đại lượng
Tỉ số của hai đại lượng cùng loại và cùng đơn vị đo là tỉ số giữa hai số đo của hai đại lượng đó.
Nhận xét:
Tỉ số của hai đại lượng thể hiện độ lớn của đại lượng này so với đại lượng kia.
Chú ý:
- Phân số $ \dfrac{a}{b}$ thì cả $ a$ và $ b$ phải là các số nguyên.
- Tỉ số $ \dfrac{a}{b}$ thì $ a$ và $ b$ có thể là các số nguyên, phân số, hỗn số, số thập phân,…
Ví dụ:
Tỉ số chiều dài hai đoạn thẳng $ AB = 1,5\,\,\,cm$ và $ CD = \dfrac{1}{3}\,cm$ là: $ 1,5:\dfrac{1}{3}$ .
Tỉ số phần trăm của a và b là $ \dfrac{a}{b}.100\% $ .
Ví dụ:
a) Tỉ số phần trăm của $ 3$ và $ 6$ là:
$ \dfrac{{3.100}}{6}\% = \dfrac{{300}}{6}\% = 50\% .$
b) Tỉ số phần trăm của $ - 2,3$ và $ 10$ là: $ \dfrac{{ - 2,3.100}}{{10}}\% = - 23\% $
Chú ý: Tỉ số $ \dfrac{{a.100}}{b}$ không nhất thiết là số nguyên.
Muốn tìm giá trị $a\% $ của số b, ta tính: $b.\,a\% = b.\dfrac{a}{{100}}$
Ví dụ:
$99,99\% $ của $3,75$ là: $3,75.\dfrac{{99,99}}{{100}} = 3,749625$
Muốn tìm mốt số khi biết $m\% $ của số đó là $b$, ta tính: $b:\dfrac{m}{{100}}$
Ví dụ:
Số có giá trị $2,5\% $ bằng $200$ là số: $200:\dfrac{{2,5}}{{100}} = 8\,000$
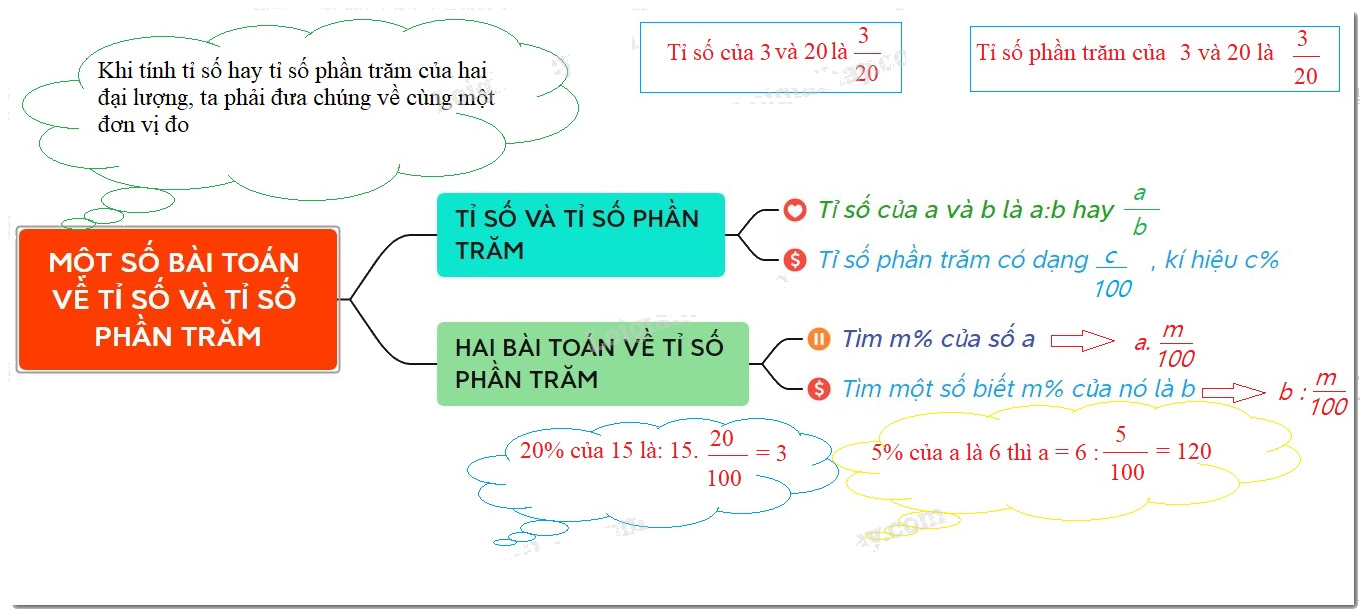
Để tính tỉ số của hai số ta tính $ a:b$ hoặc $ \dfrac{a}{b}$ $ \left( {b \ne 0} \right)$
Để tính tỉ số phần trăm của a và b, ta làm như sau:
Bước 1. Viết tỉ số $ \dfrac{a}{b}$
Bước 2. Tính số $ \dfrac{{a.100}}{b}$ và viết thêm % vào bên phải số vừa nhận được.
- Viết một số a dưới dạng dùng kí hiệu %: \(a = \dfrac{{a.100}}{{100}} = (100.a)\% \)
- Viết \(a\% \) dưới dạng phân số: \(a\% = \dfrac{a}{{100}}\)
- Đổi số thập phân ra phân số: \(\overline {a,bc} = \dfrac{{\overline {abc} }}{{100}} = \overline {abc} \% ;\,\,\,\,\,\overline {a,{b_1}{b_2}...{b_n}} = \dfrac{{a{b_1}{b_2}...{b_n}}}{{{{10}^n}}}\)
- Một phân số tối giản có mẫu số chỉ có ước số nguyên tố là 2 hoặc 5 thì có thể viết dưới dạng số thập phân (hữu hạn).
Tỉ số phần trăm thường được sử dụng trong đời sống để giải quyết một số bài toán như:- Mua bán hàng ngày
- Lãi suất tín dụng
- Thành phần các chất hóa học.
Tỉ số và tỉ số phần trăm là những khái niệm cơ bản trong toán học, được ứng dụng rộng rãi trong cuộc sống hàng ngày. Việc nắm vững kiến thức về tỉ số và tỉ số phần trăm không chỉ giúp các em giải quyết các bài toán toán học một cách dễ dàng mà còn giúp các em hiểu rõ hơn về các mối quan hệ giữa các đại lượng trong thực tế.
Định nghĩa: Tỉ số của hai đại lượng a và b (b ≠ 0) là thương của phép chia a cho b, được viết là a : b hoặc a/b.
Ví dụ: Tỉ số của chiều dài 12cm và chiều rộng 8cm của một hình chữ nhật là 12 : 8 hoặc 3/2.
Tính chất:
Định nghĩa: Tỉ số phần trăm của hai đại lượng a và b (b ≠ 0) là thương của a và b nhân với 100%, được viết là (a/b) x 100%.
Ví dụ: Một lớp có 30 học sinh, trong đó có 15 học sinh nữ. Tỉ số phần trăm học sinh nữ trong lớp là (15/30) x 100% = 50%.
Ứng dụng: Tỉ số phần trăm được sử dụng để so sánh các đại lượng, tính phần trăm tăng hoặc giảm, tính thuế, tính lãi suất,…
Có rất nhiều dạng bài toán liên quan đến tỉ số và tỉ số phần trăm. Dưới đây là một số dạng bài toán thường gặp:
Ví dụ 1: Một cửa hàng bán một chiếc áo sơ mi với giá gốc là 200.000 đồng. Cửa hàng giảm giá 10% cho chiếc áo sơ mi đó. Hỏi giá bán chiếc áo sơ mi sau khi giảm giá là bao nhiêu?
Giải:
Ví dụ 2: Một đội bóng đá đã thi đấu 20 trận, trong đó thắng 12 trận. Hỏi tỉ số phần trăm số trận thắng của đội bóng đá đó là bao nhiêu?
Giải:
Tỉ số phần trăm số trận thắng của đội bóng đá đó là: (12/20) x 100% = 60%
Để nắm vững kiến thức về tỉ số và tỉ số phần trăm, các em cần luyện tập thường xuyên. Các em có thể tìm các bài tập trong sách giáo khoa, sách bài tập hoặc trên các trang web học toán online.
Hy vọng bài học này sẽ giúp các em hiểu rõ hơn về tỉ số và tỉ số phần trăm. Chúc các em học tốt!