Chào mừng các em học sinh đến với bài học lý thuyết về các hình tứ giác đặc biệt: Hình chữ nhật, Hình thoi, Hình bình hành và Hình thang cân trong chương trình Toán 6 KNTT. Bài học này sẽ giúp các em nắm vững định nghĩa, tính chất và dấu hiệu nhận biết của từng hình, đồng thời hiểu được ứng dụng của chúng trong thực tế cuộc sống.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, dễ hiểu, cùng với các bài tập thực hành đa dạng để các em có thể tự tin chinh phục môn Toán.
Lý thuyết Hình chữ nhật. Hình thoi. Hình bình hành. Hình thang cân Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu
I. Hình chữ nhật
1. Nhận biết hình chữ nhật
Một số yếu tố cơ bản của hình chữ nhật
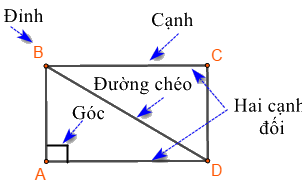
- Bốn góc bằng nhau và bằng \({90^0}\)
- Các cạnh đối bằng nhau.
- Hai đường chéo bằng nhau.
2.Cách vẽ hình chữ nhật
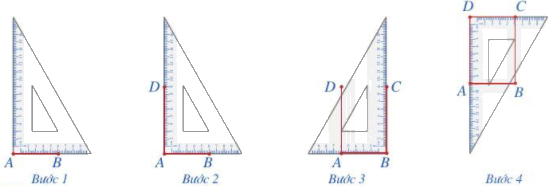
Bước 1. Vẽ theo một cạnh góc vuông của ê ke đoạn thẳng AB có độ dài bằng 6 cm
Bước 2. Đặt đỉnh góc vuông của ê ke trùng với điểm A và một cạnh ê ke nằm trên AB, vẽ theo cạnh kia của ê ke đoạn thẳng AD có độ dài bằng 9 cm
Bước 3. Xoay ê ke rồi thực hiện tương tự như ở Bước 2 để được cạnh BC có độ dài bằng 9 cm
Bước 4. Vẽ đoạn thẳng CD.
1. Một số yếu tố cơ bản của hình thoi
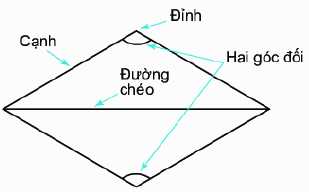
- Bốn cạnh bằng nhau
- Hai đường chéo vuông góc với nhau.
- Các cạnh đối song song với nhau
- Các góc đối bằng nhau
2. Vẽ hình thoi
Ví dụ: Dùng thước và compa vẽ hình thoi \(ABCD\), biết \(AB = 5\,cm\) và \(AC = 8\,cm\).
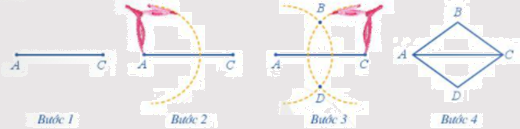
Bước 1. Dùng thước vẽ đoạn thẳng \(AC = 8\,cm\)
Bước 2. Dùng compa vẽ một phần đường tròn tâm A bán kính \(5\,cm\).
Bước 3.Dùng compa vẽ một phần đường tròn tâm C bán kính \(5\,cm\); phần đường tròn này cắt phần đường tròn tấm A vẽ ở Bước 2 tại các điểm B và D.
Bước 4. Dùng thước vẽ các đoạn thẳng AB, BC, CD, DA.
1.Nhận biết hình bình hành
Hình bình hành ABCD có:
- Bốn đỉnh A, B, C, D.
- Hai cặp cạnh đối diện bằng nhau: \(AB = CD;\,BC = AD\).
- Hai cặp cạnh đối diện song song: \(AB\) song song với \(CD\); \(BC\) song song với \(AD\).
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường: \(OA = OC;\,OB = OD.\)
- Hai góc ở các đỉnh A và C bằng nhau; hai góc ở các đỉnh B và D bằng nhau.
2.Cách vẽ hình bình hành
Ví dụ: Cho trước hai đoạn thẳng AB,AD như hình dưới đây. Vẽ hình bình hành ABCD nhận hai đoạn thẳng AB, AD làm cạnh.

Cách vẽ:
Ta có thể vẽ bằng thước và compa như sau:
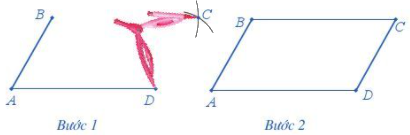
Bước 1. Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính AD. Lấy D làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB. Gọi C là giao điểm của hai phần đường tròn này
Bước 2. Dùng thước vẽ các đoạn thẳng BC và CD.
1. Nhận biết hình thang cân

Hình thang cân có:
- Hai cạnh bên bằng nhau.
- Hai đường chéo bằng nhau
- Hai đáy song song với nhau
- Hai góc kề một đáy bằng nhau.
Ví dụ:
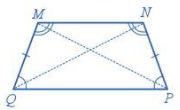
Hình thang cân \(MNPQ\) có:
- Hai cạnh cạnh đáy song song: \(MN\) song song với \(PQ\).
- Hai cạnh bên bằng nhau: \(MQ = NP\).
- Hai đường chéo bằng nhau: \(MP = NQ\).
- Hai góc kề với cạnh cạnh bên \(PQ\) bằng nhau, tức là hai góc \(NPQ\) và \(PQM\) bằng nhau; hai góc kề với cạnh bên \(MN\) bằng nhau, tức là hai góc \(QMN\) và \(MNP\) bằng nhau.
2.Cách gấp hình thang cân
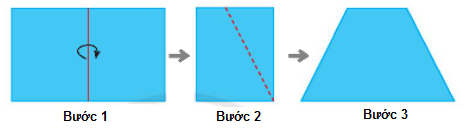
Bước 1: Gấp đôi một tờ giấy hình chữ nhật
Bước 2: Vẽ một đoạn thẳng nối hai điểm tùy ý trên hai cạnh đối diện (Cạnh không chứa nếp gấp). Cắt theo đường nét đứt như hình minh họa.
Bước 3: Mở tờ giấy ra ta được một hình thang cân.

Trong chương trình Toán 6 KNTT, việc nắm vững kiến thức về các hình tứ giác đặc biệt như hình chữ nhật, hình thoi, hình bình hành và hình thang cân là vô cùng quan trọng. Những kiến thức này không chỉ giúp các em giải quyết các bài toán hình học cơ bản mà còn ứng dụng vào thực tế cuộc sống xung quanh.
Định nghĩa: Hình chữ nhật là hình tứ giác có bốn góc vuông.
Tính chất:
Dấu hiệu nhận biết:
Định nghĩa: Hình thoi là hình tứ giác có bốn cạnh bằng nhau.
Tính chất:
Dấu hiệu nhận biết:
Định nghĩa: Hình bình hành là hình tứ giác có các cạnh đối song song.
Tính chất:
Dấu hiệu nhận biết:
Định nghĩa: Hình thang cân là hình thang có hai cạnh bên bằng nhau.
Tính chất:
Dấu hiệu nhận biết:
Các hình tứ giác đặc biệt này xuất hiện rất nhiều trong cuộc sống hàng ngày. Ví dụ:
Việc hiểu rõ về các hình này giúp chúng ta nhận biết và phân tích các vật thể xung quanh một cách chính xác hơn. Đồng thời, nó cũng là nền tảng để học các kiến thức hình học phức tạp hơn trong tương lai.
Để củng cố kiến thức, các em hãy thực hành giải các bài tập sau:
Hy vọng bài học này sẽ giúp các em nắm vững kiến thức về lý thuyết Hình chữ nhật, Hình thoi, Hình bình hành, Hình thang cân Toán 6 KNTT. Chúc các em học tập tốt!