Chào mừng bạn đến với bài học về Lý thuyết Phép chia hết, Ước và bội của một số nguyên trong chương trình Toán 6 KNTT. Bài học này sẽ giúp bạn hiểu rõ các khái niệm cơ bản, tính chất quan trọng và ứng dụng thực tế của chúng trong cuộc sống.
Chúng ta sẽ cùng nhau khám phá cách xác định một số có chia hết cho số khác, tìm ước và bội của một số, và giải các bài toán liên quan một cách dễ dàng và hiệu quả.
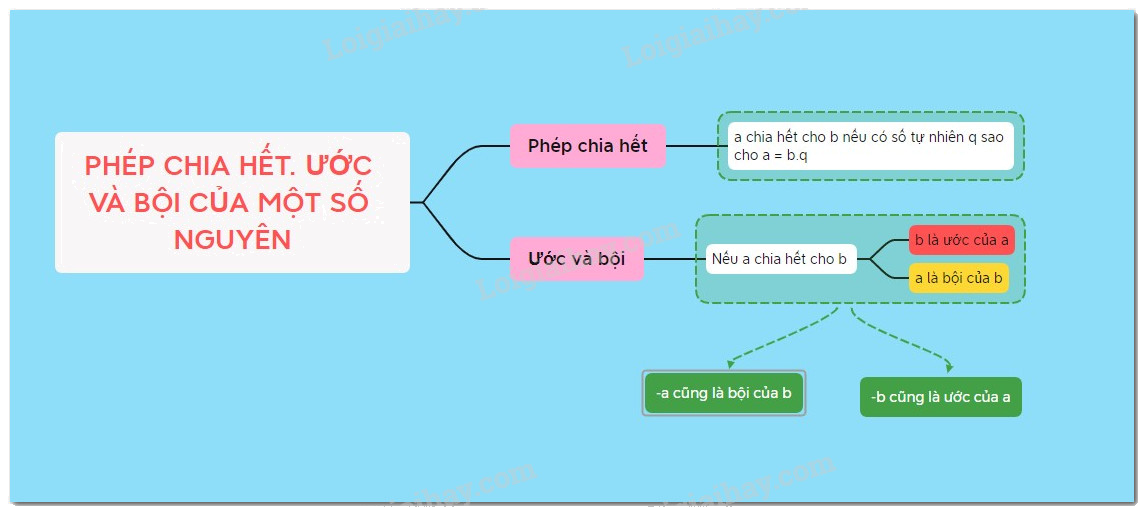
Lý thuyết Phép chia hết. Ước và bội của một số nguyên Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu
1. Phép chia hết
- Cho \(a,b \in Z\) và \(b \ne 0.\) Nếu có số nguyên \(q\) sao cho \(a = bq\) thì ta có phép chia hết
\(a:b = q\)(trong đó \(a\) là số bị chia, \(b.\) là số chia và \(q\) là thương). Khi đó ta nói \(a\)chia hết cho \(b.\) Kí hiệu \(a \vdots b\)
Ví dụ:
\(54 \vdots \left( { - 9} \right)\) vì \(54 = \left( { - 6} \right).\left( { - 9} \right)\). Ta có \(\left( {54} \right):\left( { - 6} \right) = \left( { - 9} \right)\)
\(\left( { - 63} \right) \vdots \left( { - 3} \right)\) vì \( - 63 = \left( { - 3} \right).21\). Ta có: \(\left( { - 63} \right):\left( { - 3} \right) = 21\)
2. Ước và bội
+) Khi \(a \vdots b\left( {a,b \in \mathbb{Z},b \ne 0} \right)\), ta còn gọi \(a\) là bội của \(b\) và \(b\) là ước của \((a.\)
+) Để tìm các ước của một số nguyên \(a\) bất kì ta lấy các ước nguyên dương của a cùng với số đối của chúng.
+) Ước của \( - a\) là ước của \(a\).
Chú ý:
+ Số \(0\) là bội của mọi số nguyên khác \(0.\)
+ Số \(0\) không phải là ước của bất kì số nguyên nào.
+ Các số \(1\) và \( - 1\) là ước của mọi số nguyên.
+ Nếu \(a\) là một bội của \(b\) thì \( - a\) cũng là một bội của \(b\).
+ Nếu \(b\) là một ước của \(a\) thì \( - b\) cũng là một ước của \(a\).
Ví dụ:
Tìm các ước nguyên của 6:
Ta tìm các ước nguyên dương của 6: \(1;2;3;6\)
Số đối của các số trên lần lượt là \( - 1; - 2; - 3; - 6\)
Vậy các ước nguyên của 6 là \(1; - 1;2; - 2;3; - 3;6; - 6\)
Tìm các ước nguyên của \( - 9\):
Ước nguyên của \(9\) luôn là ước nguyên của \( - 9\).
Ta tìm ước nguyên dương của 9: \(1;3;9\)
Các ước của 9 là \(1; - 1;3; - 3;9; - 9\).
Vậy các ước của \( - 9\) là \(1; - 1;3; - 3;9; - 9\).
CÁC DẠNG TOÁN VỀ PHÉP NHÂN, CHIA SỐ NGUYÊN. ƯỚC VÀ BỘI CỦA SỐ NGUYÊN
Khi thực hiện phép tính ta áp dụng các quy tắc sau:
- Quy tắc nhân hai số nguyên
Với \(m,n \in {\mathbb{N}^*}\), ta có:
\(m\left( { - n} \right) = \left( { - n} \right)m = - (m.m)\)
\(\left( { - m} \right)\left( { - n} \right) = \left( { - n} \right)\left( { - m} \right) = mn\)
- Quy tắc dấu của thương:
\(\begin{array}{l}\left( + \right):\left( + \right) = \left( + \right)\\\left( - \right):\left( - \right) = \left( + \right)\\\left( + \right):\left( - \right) = \left( - \right)\\\left( - \right):\left( + \right) = \left( - \right)\end{array}\)
Chú ý:
+ Nếu đổi dấu một thừa số thì tích $ab$ đổi dấu.
+ Nếu đổi dấu hai thừa số thì tích $ab$ không thay đổi.
Chú ý trên vẫn đúng với phép chia.
Bước 1: Căn cứ vào đề bài, suy luận để đưa về phép nhân (chia) hai số nguyên.
Bước 2: Thực hiện phép nhân (chia) hai số nguyên.
Bước 3: Kết luận.
Phương pháp
- Phân tích số nguyên $a$ thành tích hai số nguyên bằng tất cả các cách có thể.
- Từ đó tìm được $x,y.$
Ví dụ:
Tìm số nguyên \(x,y\) thỏa mãn \(\left( {x - 1} \right)\left( {y + 1} \right) = 3\)
Ta có: \(3 = ( - 1).( - 3) = 1.3\) nên ta có 4 trường hợp sau:
TH1: \(x - 1 = - 1\) và \(y + 1 = - 3\) suy ra \(x = 0\) và \(y = - 4\)
TH2: \(x - 1 = - 3\) và \(y + 1 = - 1\) suy ra \(x = - 2\) và \(y = - 2\)
TH3: \(x - 1 = 1\) và \(y + 1 = 3\) suy ra \(x = 2\) và \(y = 2\)
TH4: \(x - 1 = 3\) và \(y + 1 = 1\) suy ra \(x = 4\) và \(y = 0\)
Vậy \(\left( {x;y} \right) \in \left\{ {\left( {0;\,\, - 4} \right);\,\left( { - 2;\, - 2} \right);\left( {2;\,2} \right);\left( {4;0} \right)} \right\}\).
- Bài toán tìm x:
+ Muốn tìm số hạng ta lấy tích chia cho số hạng còn lại.
+ Muốn tìm số chia ta lấy số bị chia chia cho thương.
+ Muốn tìm số bị chia ta lấy thương nhân số chia.
- Dạng toán \(A.B=0\)
+ Nếu $A.B = 0$ thì $A = 0$ hoặc $B = 0.$
+ Nếu $A.B = 0$ mà $A$ (hoặc $B$ ) khác $0$ thì $B$ ( hoặc $A$ ) bằng $0.$
Ví dụ: Tìm \(x\) biết: \(\left( {x - 2} \right).\left( {x + 5} \right) = 0\)
\(\left( {x - 2} \right).\left( {x + 5} \right) = 0 \Rightarrow \)\(x - 2 = 0\) hoặc \(x + 5 = 0\)
Suy ra \(x = 2\) hoặc \(x = - 5\)
Vậy \(x \in \left\{ {2;\, - 5} \right\}\).
Phương pháp:
Bước 1: Quan sát biểu thức và nhận xét về tính chất của các số hạng và thừa số
Bước 2: Áp dụng các tính chất giao hoán, kết hợp và tính chất phân phối của phép nhân đối với phép cộng để tính toán được thuận lợi, dễ dàng.
Sử dụng các tính chất sau đây:
\(a.0 = 0\)
\(a.b = b.a\)
$a.\left( {b + c} \right) = ab + ac.$
$a.\left( {b - c} \right) = ab-ac.$
Ví dụ:
a) Tính nhanh: \(A = ( - 4).74.25\)
\(\begin{array}{l}A = ( - 4).74.25\\A = ( - 4).25.74\\A = - 100.74\\A = - 7400\end{array}\)
b) Tính hợp lí: \(B = 30.\left( { - 125} \right) + 25.30\)
\(\begin{array}{l}B = 30.\left( { - 125} \right) + 25.30\\B = 30.\left[ {\left( { - 125} \right) + 25} \right]\\B = 30.\left( { - 100} \right)\\B = - 3000.\end{array}\).
Phương pháp:
- Tìm các bội của một số nguyên cho trước.
Dạng tổng quát của số nguyên $a$ là $a.m$$(m \in Z).$
- Tìm tất cả các ước của một số nguyên cho trước
+ Nếu số nguyên đã cho có thể nhẩm được các ước thì ta ưu tiên cách này.
+ Nếu số nguyên đã cho có nhiều ước hoặc khó để nhẩm thì ta phân tích số đó ra thừa số nguyên tố, từ đó tìm tất cả các ước của số đã cho.
Chú ý: Ta tìm các ước dương trước từ đó suy ra các ước âm.
Ví dụ:
a) Tìm các bội nguyên của 4.
Ta lấy 4 nhân lần lượt với các số nguyên: \(..; - \,2;\, - 1;0;1;2;..\)
Các bội nguyên của 4 là: \(..; - 8; - 4;\,0\,;\,4;\,8;..\)
b) Tìm các ước nguyên của 24
Phân tích 24 ra thừa số nguyên tố ta được: \(24 = {2^3}.3\)
Suy ra các ước nguyên của 24 là: \( \pm 1; \pm 2;\,\, \pm 3;\, \pm 4; \pm 6 \pm 8;\,\, \pm 12;\, \pm 24\).
Phương pháp:
Sử dụng định nghĩa $a = b.q$ $ \Leftrightarrow a \vdots b$ $\left( {a,b,q \in Z;b \ne 0} \right)$ và các tính chất giao hoán, kết hợp, phân phối của phép nhân đối với phép cộng, tính chất chia hết của một tổng.
Ví dụ:
Cho \(A = 24m + 21n\,\); \(m,n \in \mathbb{Z}\) chứng minh A chia hết cho 3.
Cách 1:
Ta có \(24m \vdots 3\) và \(21n \vdots 3\) suy ra \(A=\left( {24m + 21n\,} \right) \vdots 3\)
Cách 2: \(A = 24m + 21n\, = 3.8m + 3.7n = 3.\left( {8m + 7m} \right) \vdots 3\). Vậy \(A \vdots 3\).
Phương pháp:
- Dạng: biểu thức có dạng tổng các số hạng thì ta áp dụng tính chất:
Nếu $a + b$ chia hết cho $c$ và $a$ chia hết cho $c$ thì $b$ chia hết cho $c.$
- Dạng: Tìm x để \({\rm{a}} \vdots A(x)\) thì \(A(x) \in \)Ư(a), giải các trường hợp ta tìm được các giá trị của \(x\).
Ví dụ:
Tìm \(x\) để \(5 \vdots \left( {x - 2} \right)\)
\(5 \vdots \left( {x - 2} \right) \Rightarrow \left( {x - 2} \right) \in \)Ư(5) \( \Rightarrow \) \(\left( {x - 2} \right) \in \left\{ { - 1;1;5; - 5} \right\} \Rightarrow x \in \left\{ {1;3;7; - 3} \right\}\)
Vậy \(x \in \left\{ {1;3;7; - 3} \right\}\).
Trong chương trình Toán 6, kiến thức về phép chia hết, ước và bội đóng vai trò nền tảng cho việc hiểu và giải quyết các bài toán số học phức tạp hơn. Bài viết này sẽ cung cấp một cái nhìn toàn diện về các khái niệm này, cùng với các ví dụ minh họa và bài tập thực hành để giúp bạn nắm vững kiến thức.
Một số a được gọi là chia hết cho số b (b ≠ 0) nếu có một số nguyên q sao cho a = bq. Ký hiệu: a ⋮ b. Số b được gọi là ước của a, và a được gọi là bội của b.
Ước của một số nguyên a là những số nguyên b sao cho a ⋮ b. Tập hợp các ước của a thường được ký hiệu là Ư(a).
Ví dụ: Ư(12) = {1, 2, 3, 4, 6, 12}.
Bội của một số nguyên a là những số nguyên b sao cho b ⋮ a. Tập hợp các bội của a thường được ký hiệu là B(a).
Ví dụ: B(3) = {..., -6, -3, 0, 3, 6, 9, ...}.
Kiến thức về phép chia hết, ước và bội có nhiều ứng dụng thực tế trong cuộc sống, ví dụ:
Để hiểu sâu hơn về phép chia hết, ước và bội, bạn có thể tìm hiểu thêm về các khái niệm liên quan như số nguyên tố, phân tích một số ra thừa số nguyên tố, ước chung lớn nhất (UCLN), bội chung nhỏ nhất (BCNN). Những kiến thức này sẽ giúp bạn giải quyết các bài toán số học phức tạp hơn một cách hiệu quả.
Lý thuyết Phép chia hết, Ước và bội của một số nguyên là một phần quan trọng trong chương trình Toán 6. Việc nắm vững kiến thức này không chỉ giúp bạn giải quyết các bài toán trong sách giáo khoa mà còn ứng dụng vào thực tế cuộc sống. Hãy luyện tập thường xuyên và tìm hiểu thêm các kiến thức liên quan để nâng cao khả năng giải toán của mình.