Bài học về Lý thuyết Làm tròn và Ước lượng Toán 6 KNTT không chỉ cung cấp kiến thức nền tảng mà còn giúp học sinh kết nối toán học với các tình huống thực tế trong cuộc sống hàng ngày.
Tại giaitoan.edu.vn, chúng tôi mang đến phương pháp học toán online hiệu quả, giúp học sinh dễ dàng tiếp thu và vận dụng kiến thức một cách linh hoạt.
Lý thuyết Làm tròn và ước lượng Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu
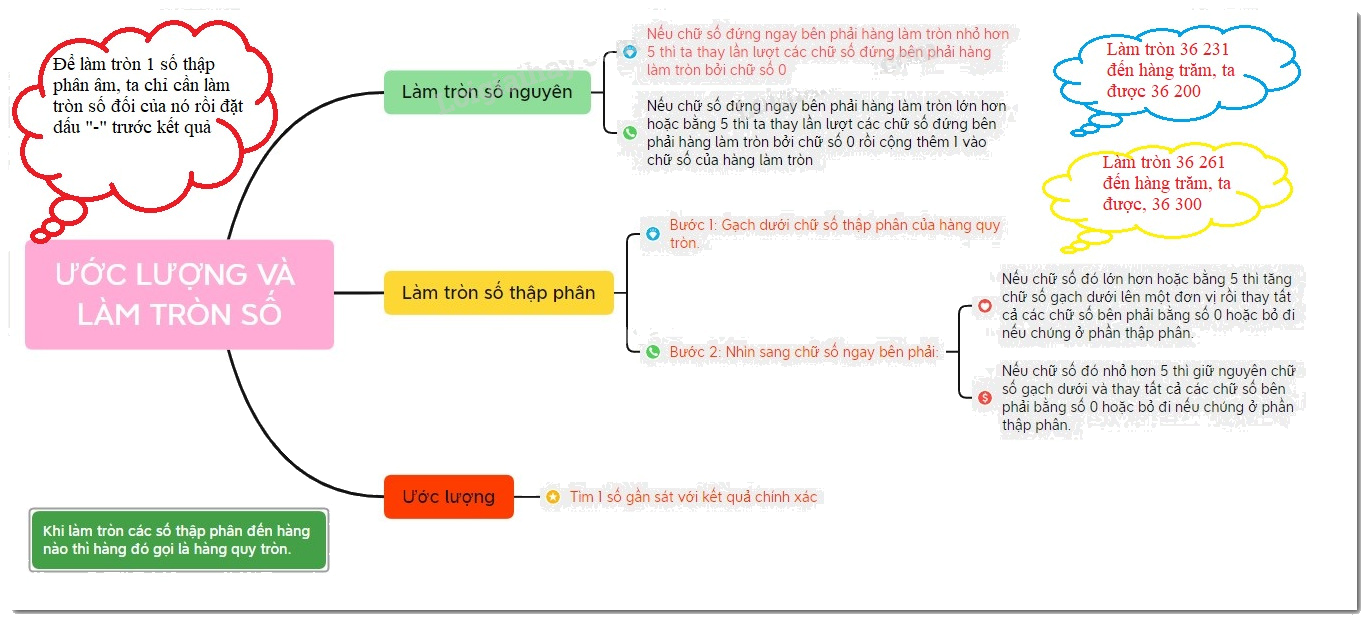
1. Làm tròn
*Làm tròn số thập phân
Để làm tròn số thập phân dương tới một hàng nào đó ( gọi là hàng làm tròn), ta làm như sau:
- Đối với chữ số hàng làm tròn:
+ Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;
+Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5
- Đối với chữ số sau hàng làm tròn:
+ Bỏ đi nếu ở phần thập phân;
+ Thay bằng các chữ số 0 nếu ở phần số nguyên
Ví dụ:
Làm tròn số $24,037$ đến hàng phần mười (đến chữ số thập phân thứ nhất).
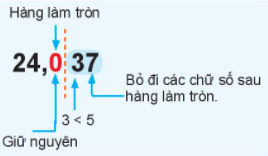
Làm tròn số đến hàng phần mười ta được kết quả là $24,0$
Vậy: $24,037 \approx 24,0$.
* Làm tròn số nguyên
Nếu chữ số đứng ngay bên phải hàng làm tròn nhỏ hơn 5 thì ta thay lần lượt các chữ số đứng bên phải hàng làm tròn bởi chữ số 0
Ví dụ: Số 134 261 làm tròn đến hàng nghìn là số 134 000 ( vì chữ số 2 bên phải hàng nghìn nhỏ hơn 5)
Nếu chữ số đứng ngay bên phải hàng làm tròn lớn hơn hoặc bằng 5 thì ta thay lần lượt các chữ số đứng bên phải hàng làm tròn bởi chữ số 0 rồi cộng thêm 1 vào chữ số của hàng làm tròn
Ví dụ: Số 134 761 làm tròn đến hàng nghìn là số 135 000 ( vì chữ số 7 bên phải hàng nghìn lớn hơn 5)
Chú ý: Để làm tròn 1 số thập phân âm, ta chỉ cần làm tròn số đối của nó rồi đặt dấu "-" trước kết quả
Chú ý: Kí hiệu “ \(\approx\)” đọc là “gần bằng” hoặc “xấp xỉ”.
Ví dụ: Làm tròn số $125\,\,356$ đến hàng nghìn
Do chữ số hàng trăm là $3$ nên: $125\,\,356 \approx 125\,\,000$
Ta có thể sử dụng quy ước làm tròn số để ước lượng kết quả các phép tính. Nhờ đó có thể dễ dàng phát hiện ra những đáp số không hợp lí.
Ví dụ:
Ước lượng kết quả các phép tính sau:
a) $\left( { - 11,032} \right).\left( { - 24,3} \right) \approx 11.24 = 264$
b) $81.49 \approx 80.50 = 4\,000$
Trong chương trình Toán 6 KNTT, việc làm quen với các khái niệm về làm tròn và ước lượng là vô cùng quan trọng. Đây là những kỹ năng toán học cơ bản, giúp học sinh có thể xử lý các con số một cách nhanh chóng và hiệu quả, đồng thời đưa ra các quyết định hợp lý trong nhiều tình huống thực tế.
Làm tròn số là quá trình thay thế một số bằng một số gần đúng hơn, thường là số nguyên hoặc số thập phân có ít chữ số thập phân hơn. Mục đích của việc làm tròn số là để đơn giản hóa các phép tính hoặc để biểu diễn các số một cách dễ hiểu hơn.
Để làm tròn một số đến một hàng cụ thể, ta thực hiện các bước sau:
Ví dụ:
Tương tự như làm tròn số nguyên, ta cũng thực hiện các bước tương tự để làm tròn số thập phân đến một hàng cụ thể.
Ví dụ:
Ước lượng là quá trình tìm một giá trị gần đúng cho một đại lượng nào đó. Ước lượng thường được sử dụng khi ta không thể hoặc không cần thiết phải biết giá trị chính xác của đại lượng đó.
Để ước lượng kết quả của một phép tính, ta có thể làm tròn các số trước khi thực hiện phép tính. Sau đó, ta thực hiện phép tính với các số đã được làm tròn để có được kết quả ước lượng.
Ví dụ:
Ước lượng kết quả của phép tính 12,34 + 5,67:
Ước lượng được ứng dụng rộng rãi trong cuộc sống hàng ngày, ví dụ như:
Làm tròn và ước lượng có mối liên hệ mật thiết với nhau. Việc làm tròn số là một bước quan trọng trong quá trình ước lượng. Khi ta làm tròn các số, ta đang tạo ra các giá trị gần đúng, và các giá trị này được sử dụng để ước lượng kết quả của các phép tính hoặc các đại lượng khác.
Để củng cố kiến thức về Lý thuyết Làm tròn và Ước lượng Toán 6 KNTT, các em có thể thực hành các bài tập sau:
Lý thuyết Làm tròn và Ước lượng Toán 6 KNTT là một phần quan trọng của chương trình học. Việc nắm vững kiến thức này sẽ giúp học sinh có thể xử lý các con số một cách nhanh chóng và hiệu quả, đồng thời ứng dụng toán học vào các tình huống thực tế trong cuộc sống.