Bài học này cung cấp kiến thức nền tảng về quan hệ chia hết và các tính chất quan trọng của nó trong chương trình Toán 6 KNTT. Chúng ta sẽ cùng nhau khám phá cách ứng dụng những kiến thức này vào giải quyết các bài toán thực tế, giúp các em học sinh hiểu sâu hơn về môn Toán.
Nội dung bài học được trình bày một cách dễ hiểu, kèm theo nhiều ví dụ minh họa và bài tập thực hành để các em có thể tự kiểm tra và củng cố kiến thức.
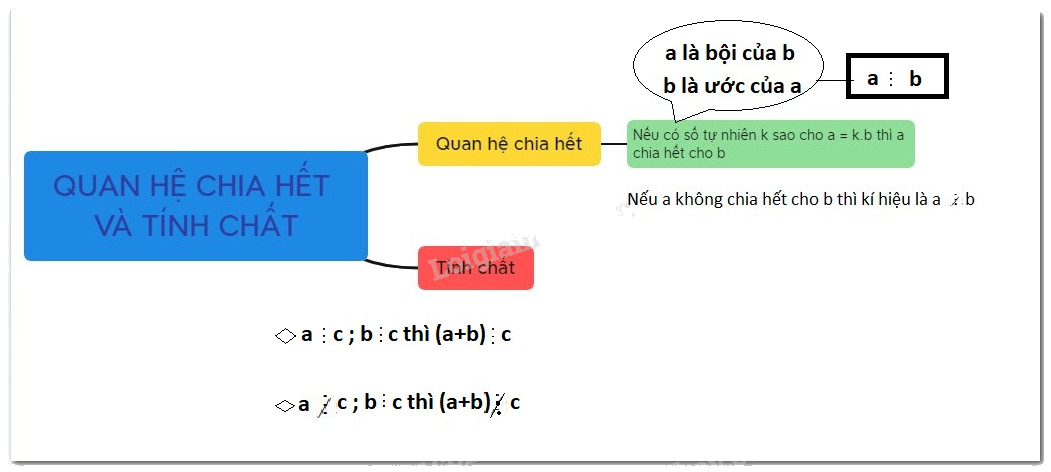
Lý thuyết Quan hệ chia hết và tính chất Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu
1. Quan hệ chia hết
Khi nào thì a chia hết cho b?
Cho hai số tự nhiên \(a\) và \(b,\) trong đó \(b \ne 0,\) nếu có số tự nhiên \(x\) sao cho \(b.x = a\) thì ta nói \(a\) chia hết cho \(b\) và ta có phép chia hết \(a:b = x\)
Nếu \(a\) không chia hết cho \(b,\) ta kí hiệu là \(a\not \vdots b\).
Ước và bội
- Nếu có số tự nhiên \(a\) chia hết cho số tự nhiên \(b\) thì ta nói \(a\) là bội của \(b,\) còn \(b\) là ước của \(a.\)
- Kí hiệu: Ư\(\left( a \right)\) là tập hợp các ước của \(a\) và \(B\left( b \right)\) là tập hợp các bội của \(b\).
Ví dụ : \(12 \vdots 6 \Rightarrow 12\) là bội của \(6.\) Còn \(6\) được gọi là ước của \(12\)
Cách tìm ước và bội
Tìm ước:
- Ta có thể tìm các ước của \(a\)\(\left( {a > 1} \right)\) bằng cách lần lượt chia \(a\) cho các số tự nhiên từ \(1\) đến \(a\) để xét xem \(a\) chia hết cho những số nào, khi đó các số ấy là ước của \(a.\)
Ví dụ :
16:1=16; 16:2=8; 16:4=4; 16:8=2; 16:16=1
Vậy các ước của 16 là 1;2;4;8;16. Tập hợp các ước của 16 là:
Ư\(\left( {16} \right) = \left\{ {1;2;4;8;16} \right\}\)
Tìm bội:
- Ta có thể tìm các bội của một số khác \(0\) bằng cách nhân số đó lần lượt với \(0,1,2,3,...\)
Ví dụ :
Ta lấy 6 nhân với từng số 0 thì được 0 nên 0 là bội của 6, lấy 6.1=6 nên 6 là bội của 6, 6.2=12 nên 12 là bội của 6,...
Vậy \(B\left( 6 \right) = \left\{ {0;6;12;18;...} \right\}\)
2. Tính chất chia hết của một tổng
- Tính chất 1: Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.
\(a \vdots m\) và \(b \vdots m\) \( \Rightarrow \left( {a + b} \right) \vdots m\)
\(a\, \vdots \,m;\,b \vdots m;\,c \vdots m \Rightarrow \left( {a + b + c} \right) \vdots m\)
- Tính chất 2: Nếu chỉ có một số hạng của tổng không chia hết cho một số, còn các số hạng khác đều chia hết cho số đó thì tổng không chia hết cho số đó.
\(a \vdots m\) và \(b\not \vdots m\)\( \Rightarrow \left( {a + b} \right)\not \vdots m\)
\(a\not \vdots m;\,b \vdots m;\,c \vdots m \Rightarrow \left( {a + b + c} \right)\not \vdots m\)
Ví dụ: Ta có \(6 \vdots 3;\,9 \vdots 3;\,15 \vdots 3\, \Rightarrow 6 + 9 + 15 = 30 \vdots 3\);\(10 \vdots 5;\,15 \vdots 5;\,12\not \vdots 5 \Rightarrow 10 + 15 + 12 = 37\not \vdots 5\)
Trong chương trình Toán 6 KNTT, kiến thức về quan hệ chia hết và tính chất là một phần quan trọng, đặt nền móng cho các kiến thức nâng cao hơn ở các lớp trên. Hiểu rõ về quan hệ chia hết không chỉ giúp học sinh giải quyết các bài toán một cách hiệu quả mà còn rèn luyện tư duy logic và khả năng phân tích.
Quan hệ chia hết giữa hai số nguyên a và b (b ≠ 0) được biểu diễn là a chia hết cho b, ký hiệu là a ⋮ b. Điều này có nghĩa là tồn tại một số nguyên q sao cho a = b * q. Số a được gọi là số bị chia, b là số chia, và q là thương.
Có một số tính chất quan trọng của quan hệ chia hết mà học sinh cần nắm vững:
Chứng minh Tính chất 1:
Vì a ⋮ b nên a = b * m (m là số nguyên). Vì c ⋮ b nên c = b * n (n là số nguyên). Do đó, a + c = b * m + b * n = b * (m + n). Vì m + n là số nguyên nên (a + c) ⋮ b.
Quan hệ chia hết và tính chất của nó được ứng dụng rộng rãi trong việc giải các bài toán liên quan đến tính chia hết, tìm ước chung, ước chung lớn nhất (UCLN), và các bài toán thực tế khác.
Ví dụ 3: Chứng minh rằng 144 ⋮ 12.
Ta có: 144 = 12 * 12. Vậy 144 ⋮ 12.
Dưới đây là một số bài tập để các em luyện tập và củng cố kiến thức:
Ngoài các tính chất cơ bản đã học, các em có thể tìm hiểu thêm về các khái niệm liên quan như số nguyên tố, hợp số, phân tích một số ra thừa số nguyên tố. Những kiến thức này sẽ giúp các em hiểu sâu hơn về cấu trúc của số nguyên và ứng dụng trong nhiều lĩnh vực khác nhau.
Quan hệ chia hết không chỉ là một khái niệm toán học trừu tượng mà còn có ứng dụng thực tế trong cuộc sống hàng ngày. Ví dụ, khi chia một chiếc bánh cho nhiều người, chúng ta cần đảm bảo rằng số phần bánh chia được là số nguyên. Hoặc khi tính toán chi phí cho một dự án, chúng ta cần đảm bảo rằng tổng chi phí chia hết cho số lượng người tham gia.
Hy vọng bài học này đã giúp các em hiểu rõ hơn về lý thuyết quan hệ chia hết và tính chất trong Toán 6 KNTT. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải quyết các bài toán!