Chào mừng các em học sinh đến với bài học về Lý thuyết Mở rộng phân số và Phân số bằng nhau trong chương trình Toán 6 KNTT. Bài học này sẽ giúp các em hiểu rõ hơn về khái niệm phân số, cách so sánh và rút gọn phân số, cũng như ứng dụng của chúng trong cuộc sống hàng ngày.
Tại giaitoan.edu.vn, chúng tôi cung cấp kiến thức toán học một cách dễ hiểu, trực quan và sinh động, giúp các em học tập hiệu quả và đạt kết quả tốt nhất.
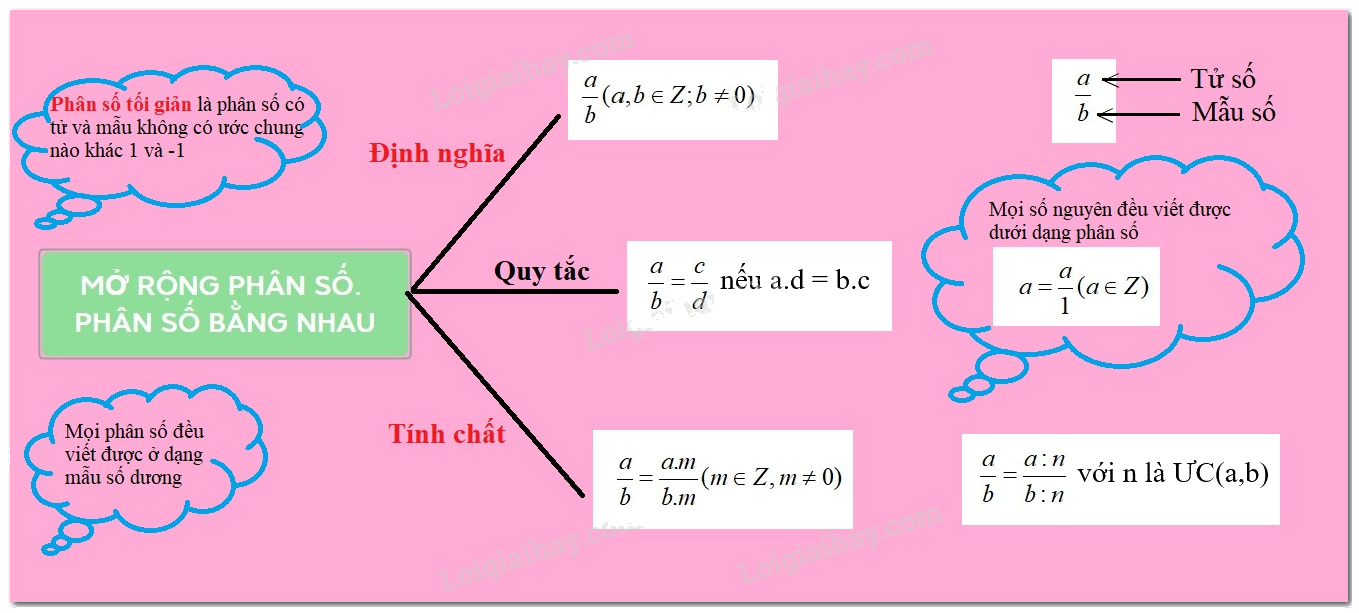
Lý thuyết Mở rộng phân số. Phân số bằng nhau Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu
Hai phân số bằng nhau
1. Mở rộng khái niệm phân số
Ta gọi \(\frac{a}{b}\), trong đó \(a,\;b \in \mathbb{Z},\;b \ne 0\)là phân số, a là tử số (tử) và b là mẫu số (mẫu) của phân số. Phân số \(\frac{a}{b}\) đọc là a phần b.
2. Hai phân số bằng nhau
Hai phân số \(\frac{a}{b}\) và \(\frac{c}{d}\) được gọi là bằng nhau, viết là \(\frac{a}{b} = \frac{c}{d}\), nếu \(a.d = b.c\).
Chú ý: Điều kiện \(a.d = b.c\) gọi là điều kiện bằng nhau của hai phân số \(\frac{a}{b}\) và \(\frac{c}{d}\).
3. Tính chất cơ bản của phân số
*Nếu ta nhân cả tử và mẫu của một phân số với cùng 1 số nguyên khác 0 thì ta được một phân số bằng phân số đã cho.
*Nếu ta chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số bằng phân số đã cho.
Chú ý: Mọi số nguyên a đều viết được dưới dạng phân số:\(\dfrac{a}{1}\)
* Phương pháp rút gọn về phân số tối giản
Bước 1: Tìm ƯCLN của tử và mẫu sau khi đã bỏ dấu – (nếu có)
Bước 2: Chia cả tử và mẫu cho ước chung lớn nhất vừa tìm được, ta có phân số tối giản cần tìm
- Sử dụng định nghĩa phân số:
Người ta gọi \(\dfrac{a}{b}\) với \(a,b \in Z;b \ne 0\) là một phân số, \(a\) là tử số (tử), \(b\) là mẫu số (mẫu) của phân số.
- Quan sát hình vẽ hoặc dựa vào các dự kiện đề bài ra để mô tả các bài toán thực tiễn qua phân số. Ý nghĩa tử số và mẫu số của phân số:+) Mẫu số cho biết đơn vị được chia ra làm mấy phần bằng nhau +) Tử số cho biết số phần bằng nhau đã lấy.
Chú ý: Mẫu của phân số phải khác 0.
- Nếu \(a.d = b.c\) thì \(\dfrac{a}{b} = \dfrac{c}{d}\);
- Nếu \(a.d \ne b.c\) thì \(\dfrac{a}{b} \ne \)\(\dfrac{c}{d}\);
Cách 1: \(\dfrac{a}{b}\) = \(\dfrac{c}{d}\) nên \(a.d = b.c\) (định nghĩa hai phân số bằng nhau)
Suy ra \(a = \dfrac{{b.c}}{d}\) , \(d = \dfrac{{b.c}}{a}\) , \(b = \dfrac{{a.d}}{c}\) , \(c = \dfrac{{a.d}}{b}.\)
Cách 2: Áp dụng tính chất cơ bản của phân số để biến đổi hai phân số đã cho thành hai phân số bằng chúng nhưng có từ (hoặc mẫu) như nhau. Khi đó mẫu (hoặc tử) của chúng phải bằng nhau. Từ đó tìm được số chưa biết.
Từ định nghĩa phân số bằng nhau ta có:
\(a.d = b.c\) \( \Rightarrow \) \(\dfrac{a}{b}\) = \(\dfrac{c}{d}\) ;
\(a.d = c.b\) \( \Rightarrow \) \(\dfrac{a}{c}\) = \(\dfrac{b}{d}\) ;
\(d.a = b.c\) \( \Rightarrow \) \(\dfrac{d}{b}\) = \(\dfrac{c}{a}\) ;
\(d.a = c.b\) \( \Rightarrow \) \(\dfrac{d}{c}\) = \(\dfrac{b}{a}\) ;
Áp dụng tính chất cơ bản của phân số
$\dfrac{a}{b} = \dfrac{{a.m}}{{b.m}}$ với $m \in Z$ và $m \ne 0$; $\dfrac{a}{b} = \dfrac{{a:n}}{{b:n}}$với $n \in $ ƯC$\left( {a;b} \right)$.
Ta thực hiện hai bước:
- Rút gọn phân số đã cho đến tối giản, chằng hạn ta được phân số tối giản $\dfrac{m}{n}$ ;
- Dạng tổng quát của các phân số phải tìm là $\dfrac{{m.k}}{{n.k}}$ ($k$$ \in $$\mathbb{Z}$, $k$$ \ne 0).$
Phân số là một khái niệm cơ bản trong toán học, xuất hiện rất nhiều trong cuộc sống hàng ngày. Hiểu rõ về phân số, đặc biệt là lý thuyết mở rộng phân số và phân số bằng nhau, là nền tảng quan trọng để học tốt các kiến thức toán học nâng cao hơn.
Phân số là biểu thức của một hoặc nhiều phần bằng nhau của một đơn vị. Một phân số được viết dưới dạng a/b, trong đó:
Ví dụ: 1/2, 3/4, 5/7 là các phân số.
Lý thuyết mở rộng phân số cho phép chúng ta tạo ra các phân số bằng nhau bằng cách nhân cả tử số và mẫu số của một phân số với cùng một số khác 0. Điều này rất hữu ích trong việc so sánh và quy đồng mẫu số của các phân số.
Ví dụ: 1/2 = (1 x 2) / (2 x 2) = 2/4 = (1 x 3) / (2 x 3) = 3/6. Tất cả các phân số 1/2, 2/4, 3/6 đều bằng nhau.
Hai phân số được gọi là bằng nhau nếu chúng biểu diễn cùng một lượng. Để kiểm tra hai phân số có bằng nhau hay không, chúng ta có thể sử dụng phương pháp nhân chéo:
Nếu a/b = c/d thì a x d = b x c.
Ví dụ: 2/3 = 4/6 vì 2 x 6 = 3 x 4 (12 = 12).
Những kiến thức này không chỉ quan trọng trong toán học mà còn ứng dụng rất nhiều trong cuộc sống:
Hãy thử giải các bài tập sau để củng cố kiến thức:
Lý thuyết Mở rộng phân số và Phân số bằng nhau là những kiến thức nền tảng quan trọng trong chương trình Toán 6 KNTT. Việc nắm vững những kiến thức này sẽ giúp các em học tập tốt hơn và ứng dụng vào giải quyết các bài toán thực tế một cách hiệu quả. Hãy luyện tập thường xuyên để củng cố kiến thức và đạt kết quả tốt nhất!
| Phân số | Rút gọn |
|---|---|
| 4/8 | 1/2 |
| 6/9 | 2/3 |
| 10/15 | 2/3 |
| Bảng ví dụ về rút gọn phân số | |