Quy tắc dấu ngoặc là một trong những kiến thức cơ bản và quan trọng trong chương trình Toán 6. Việc nắm vững quy tắc này giúp học sinh giải quyết các bài toán một cách chính xác và hiệu quả. Bài viết này sẽ cung cấp cho bạn lý thuyết đầy đủ, dễ hiểu về quy tắc dấu ngoặc, cùng với các ví dụ minh họa và bài tập thực hành.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng online chất lượng cao, giúp học sinh hiểu sâu sắc kiến thức và tự tin làm bài tập.
Lý thuyết Quy tắc dấu ngoặc Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu
1. Phép trừ hai số nguyên
Muốn trừ số nguyên \(a\) cho số nguyên \(b\), ta cộng \(a\) với số đối của b:
\(a - b = a + \left( { - b} \right)\)
Nhận xét: Phép trừ trong \(\mathbb{N}\) không phải bao giờ cũng thực hiện được, còn phép trừ trong \(\mathbb{Z}\) luôn thực hiện được.
Chú ý: Cho hai số nguyên \(a\) và \(b\). Ta gọi \(a - b\) là hiệu của \(a\) và \(b\) (\(a\) được gọi là số bị trừ, \(b\) là số trừ).
Ví dụ 1:
a) \(6 - 9 = 6 + \left( { - 9} \right) = - \left( {9 - 6} \right) = - 3\).
b) \(8 - \left( { - 4} \right) = 8 + 4 = 12\).
c) \( - 8 - \left( { - 9} \right) = - 8 + 9 = 9 - 8 = 1\).
Ví dụ 2:
Nhiệt độ trong phòng ướp lạnh đang là \({3^o}C\), bác Nhung vặn nút điều chỉnh giảm \({4^O}C\).Nhiệt độ phòng sau khi giảm là bao nhiêu độ.
Giải
Do bác Nhung giảm nhiệt độ đi \({4^o}C\), nên ta làm phép trừ:
\(3 - 4 = 3 + \left( { - 4} \right) = - \left( {4 - 3} \right) = - 1\).
Vậy nhiệt độ phòng ướp lạnh sau khi giảm là \( - {1^o}C\).
Khi bỏ dấu ngoặc, nếu đằng trước dấu ngoặc:
- Có dấu “+”, thì vẫn giữ nguyên dấu của các số hạng trong ngoặc
\( + \left( {a + b - c} \right) = a + b - c\)
- Có dấu “-”, thì phải đổi dấu tất cả các số hạng trong ngoặc
\( - \left( {a + b - c} \right) = - a - b + c\)
Chú ý:
Trong một biểu thức, ta có thể:
+ Thay đổi tùy ý vị trí của các số hạng kèm theo dấu của chúng.
\(a - b - c = - b + a - c = - c - b + a.\)
+ Đặt dấu ngoặc để nhóm các số hạng một cách tùy ý. Nếu trước dấu ngoặc là dấu “-” thì phải đổi dấu tất cả các số hạng trong ngoặc.
\(a - b - c = \left( {a - b} \right) - c = a - \left( {b + c} \right).\)
Ví dụ 1:
\(\begin{array}{l}673 + \left[ {2021 - \left( {2021 + 673} \right)} \right] = 673 + \left[ {2021 - 2021 - 673} \right]\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 673 + \left( { - 673} \right) = 0\end{array}\)
Ví dụ 2:
\(\begin{array}{l}12 + 13 + 14 - 15 - 16 - 17 = \left( {12 - 15} \right) + \left( {13 - 16} \right) + \left( {14 - 17} \right)\\ = \left( { - 3} \right) + \left( { - 3} \right) + \left( { - 3} \right) = - \left( {3 + 3 + 3} \right) = - 9\end{array}\).
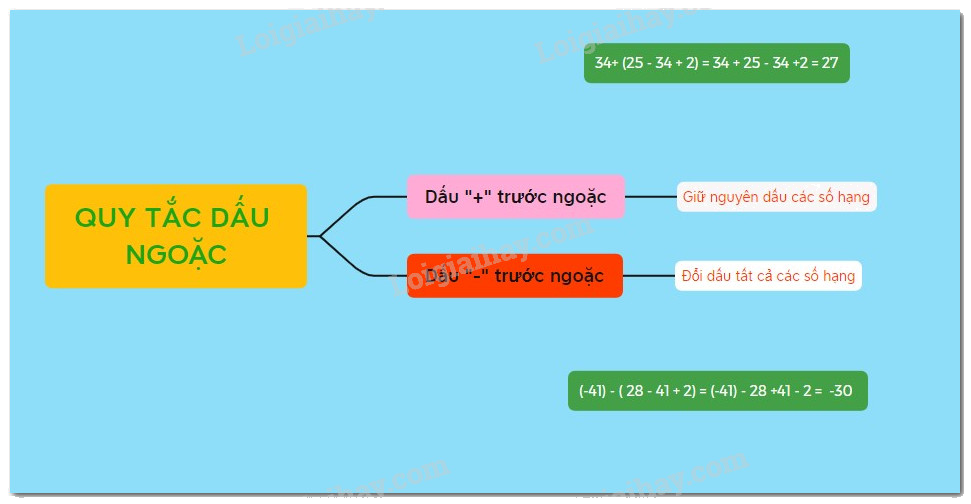
Quy tắc dấu ngoặc là một phần không thể thiếu trong chương trình Toán 6, đặc biệt là khi học về các phép tính với số nguyên. Hiểu rõ quy tắc này giúp học sinh tránh được những sai sót không đáng có và xây dựng nền tảng vững chắc cho các kiến thức toán học nâng cao hơn.
Dấu ngoặc trong toán học được sử dụng để nhóm các số hạng hoặc biểu thức lại với nhau, nhằm chỉ rõ thứ tự thực hiện các phép tính. Có ba loại dấu ngoặc phổ biến:
Khi một biểu thức chứa nhiều loại dấu ngoặc khác nhau, ta thực hiện các phép tính theo thứ tự: ngoặc tròn, ngoặc vuông, ngoặc nhọn.
Quy tắc dấu ngoặc quy định cách bỏ dấu ngoặc và đổi dấu các số hạng bên trong dấu ngoặc:
Ví dụ 1: Tính giá trị của biểu thức: 5 + (3 - 2)
Giải:
5 + (3 - 2) = 5 + 1 = 6
Ví dụ 2: Tính giá trị của biểu thức: 7 - (4 + 1)
Giải:
7 - (4 + 1) = 7 - 5 = 2
Ví dụ 3: Tính giá trị của biểu thức: - (2 - 5)
Giải:
- (2 - 5) = - (-3) = 3
Hãy tính giá trị của các biểu thức sau:
Trong các biểu thức phức tạp hơn, ta cần kết hợp quy tắc dấu ngoặc với thứ tự thực hiện các phép tính (nhân, chia trước; cộng, trừ sau). Ví dụ:
2 x (5 + 3) - 10 = 2 x 8 - 10 = 16 - 10 = 6
Quy tắc dấu ngoặc không chỉ quan trọng trong toán học mà còn có ứng dụng trong nhiều lĩnh vực khác của cuộc sống, chẳng hạn như:
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về lý thuyết quy tắc dấu ngoặc Toán 6 KNTT với cuộc sống. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải quyết các bài toán!