Chào mừng các em học sinh đến với bài học về Lý thuyết Xác suất thực nghiệm Toán 6 KNTT. Bài học này sẽ giúp các em hiểu rõ về khái niệm xác suất, cách tính xác suất thực nghiệm và ứng dụng của nó trong cuộc sống hàng ngày.
Chúng ta sẽ cùng nhau khám phá những ví dụ minh họa sinh động, giúp các em dễ dàng nắm bắt kiến thức và tự tin giải các bài tập liên quan.
Lý thuyết Xác suất thực nghiệm Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu
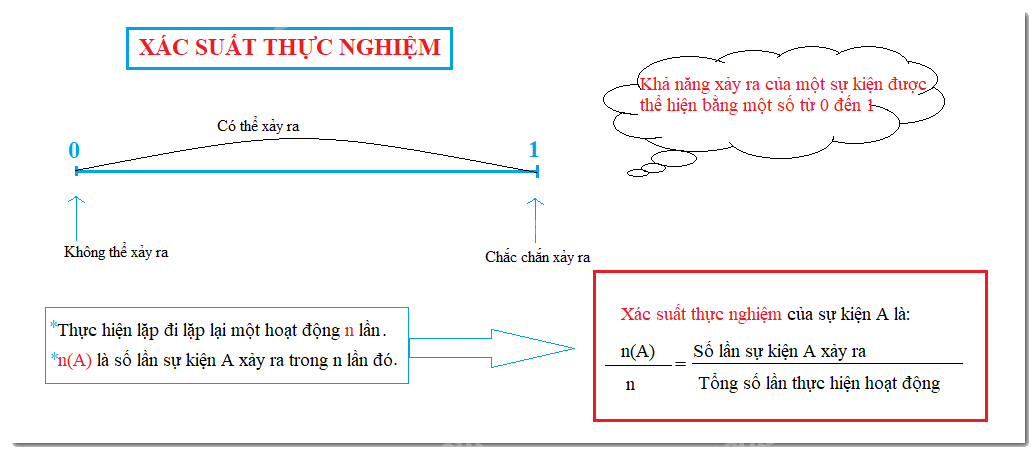
Khả năng của một sự kiện được thể hiện bằng một con số từ 0 đến 1.
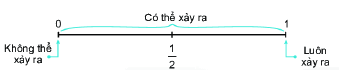
Một sự kiện không thể xảy ra có khả năng xảy ra bằng 0.
Một sự kiện chắc chắn xảy ra có khả năng xảy ra bằng 1.
Thực hiện lặp đi lặp lại một hoạt động nào đó n lần.
Gọi n(A) là số lần sự kiện A xảy ra trong n lần đó. Tỉ số
\(\frac{{n(A)}}{n} = \) Số lần sự kiện A xảy ra : Tổng số lần thực hiện hoạt động
Được gọi là xác suất thực nghiệm của sự kiện A.
Nhận xét:Xác suất thực nghiệm phụ thuộc vào người thực hiện thí nghiệm, trò chơi và số lần người đó thực hiện thí nghiệm, trò chơi.
Ví dụ:
Vuông gieo một đồng xu 55 lần và thấy có 30 lần xuất hiện mặt sấp. Tròn lấy đồng xu đó gieo 100 lần và thấy có 45 lần xuất hiện mặt sấp.
Hãy tính xác suất thực nghiệm của sự kiện “Đồng xu xuất hiện mặt sấp” trong 2 thí nghiệm trên và so sánh hai xác suất thực nghiệm đó.
Giải:
Vuông:
Số lần gieo được mặt sấp là 30. Tổng số lần gieo là 55 nên xác suất thực nghiệm của sự kiện “Đồng xu xuất hiện mặt sấp” là: \(\dfrac{{30}}{{55}}\).
Tròn:
Số lần gieo được mặt sấp là 45, tổng số lần gieo là 100. Xác suất thực nghiệm của sự kiện “Đồng xu xuất hiện mặt sấp” là: \(\dfrac{{45}}{{100}}\).
Ta thấy Vuông và Tròn thực hiện hai thí nghiệm với tổng số lần gieo khác nhau và nhận được xác suất thực nghiệm của sự kiện “Đồng xu xuất hiện mặt sấp” là khác nhau.
Phương pháp:
Bước 1: Xác định số lần được kết quả A (kết quả cần tính xác suất) và tổng số lần gieo.
Bước 2: Sử dụng công thức sau để tính xác suất:
\(\frac{{n(A)}}{n} = \) Số lần sự kiện A xảy ra : Tổng số lần thực hiện hoạt động
Ví dụ: Gieo một con xúc xắc sáu mặt 7 lần và số chấm xuất hiện của mỗi lần gieo như sau:
Lần 1 | Lần 2 | Lần 3 | Lần 4 | Lần 5 | Lần 6 | Lần 7 |
1 | 1 | 5 | 6 | 3 | 3 | 4 |
Bước 1: Số lần gieo được mặt 3 chấm là 2 lần. Tổng số lần gieo là 7.
Bước 2: Xác suất mặt 3 chấm xuất hiện là \(\dfrac{2}{7}\)
Bài 1. Gieo một con xúc xắc 6 mặt 50 lần ta được kết quả như sau:
Mặt | 1 chấm | 2 chấm | 3 chấm | 4 chấm | 5 chấm | 6 chấm |
Số lần | 8 | 7 | 3 | 12 | 10 | 10 |
Hãy tính xác suất thực nghiệm của sự kiện gieo được mặt có số lẻ chấm trong 50 lần gieo trên.
A. 0,21
B. 0,44
C. 0,42
D. 0,18
Lời giải: Tổng số lần gieo là 50.
Các mặt có số lẻ chấm của con xúc xắc là mặt 1, 3 và 5.
Số lần được mặt 1 chấm là 8 lần, mặt 3 chấm là 3 lần, mặt 5 chấm là 10 lần.
Số lần được mặt có số lẻ chấm là 8+3+10=21 lần
Xác suất thực nghiệm của sự kiện gieo được mặt có số lẻ chấm trong 50 lần là:
\(\dfrac{{21}}{{50}} = 0,42\)
Chọn đáp án C
Bài 2. Nếu tung một đồng xu 22 lần liên tiếp thì, có 14 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng bao nhiêu?
A. \(\dfrac{7}{{11}}\)
B. \(\dfrac{4}{{11}}\)
C. \(\dfrac{4}{7}\)
D. \(\dfrac{3}{7}\)
Lời giải:
Tổng số lần gieo là 22.
Số lần gieo được mặt N là 14.
Xác suất thực nghiệm xuất hiện mặt N là: \(\dfrac{{14}}{{22}} = \dfrac{7}{{11}}\)
Chọn đáp án A.
Bài 3. Nếu tung một đồng xu 30 lần liên tiếp có 12 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt S bằng bao nhiêu?
A. \(\dfrac{2}{5}\)
B. \(\dfrac{1}{5}\)
C. \(\dfrac{3}{5}\)
D. \(\dfrac{3}{4}\)
Lời giải:
Tổng số lần gieo là 30.
Số lần gieo được mặt S là 30-12=18.
Xác suất thực nghiệm xuất hiện mặt S là: \(\dfrac{{18}}{{30}} = \dfrac{3}{5}\)
Chọn đáp án C.
Bài 4. Gieo một con xúc xắc 20 lần liên tiếp, có 6 lần xuất hiện mặt 3 chấm thì xác suất thực nghiệm xuất hiện mặt 3 chấm bằng
A. 0,15
B. 0,3
C. 0,6
D. 0,36
Lời giải: Tổng số lần gieo là 20, số lần xuất hiện mặt 3 chấm là 6 lần.
Xác suất thực nghiệm xuất hiện mặt 3 chấm bằng \(\dfrac{6}{{20}} = 0,3\).
Chọn đáp án B.
Xác suất thực nghiệm là một khái niệm quan trọng trong toán học, giúp chúng ta dự đoán khả năng xảy ra của một sự kiện dựa trên kết quả của các thử nghiệm thực tế. Trong chương trình Toán 6 KNTT, học sinh được giới thiệu về khái niệm này thông qua các ví dụ đơn giản và gần gũi với cuộc sống.
Xác suất thực nghiệm của một sự kiện A được tính bằng tỷ lệ giữa số lần sự kiện A xảy ra và tổng số lần thực hiện thử nghiệm. Công thức tính xác suất thực nghiệm như sau:
P(A) = (Số lần sự kiện A xảy ra) / (Tổng số lần thực hiện thử nghiệm)
Ví dụ: Gieo một đồng xu 100 lần, mặt ngửa xuất hiện 52 lần. Vậy xác suất thực nghiệm của sự kiện “mặt ngửa xuất hiện” là:
P(mặt ngửa) = 52 / 100 = 0.52
Xác suất thực nghiệm được ứng dụng rộng rãi trong nhiều lĩnh vực của cuộc sống, như:
Bài 1: Một hộp có 20 quả bóng, trong đó có 8 quả bóng màu đỏ, 7 quả bóng màu xanh và 5 quả bóng màu vàng. Lấy ngẫu nhiên một quả bóng từ hộp. Tính xác suất thực nghiệm để lấy được quả bóng màu đỏ.
Giải:
Số lần thực hiện thử nghiệm: 20 (tổng số quả bóng)
Số lần sự kiện “lấy được quả bóng màu đỏ” xảy ra: 8 (số quả bóng màu đỏ)
Xác suất thực nghiệm để lấy được quả bóng màu đỏ: P(đỏ) = 8 / 20 = 0.4
Bài 2: Gieo một xúc xắc 6 mặt 50 lần. Kết quả thống kê được như sau:
| Mặt xúc xắc | Số lần xuất hiện |
|---|---|
| 1 | 7 |
| 2 | 9 |
| 3 | 8 |
| 4 | 10 |
| 5 | 6 |
| 6 | 10 |
Tính xác suất thực nghiệm để gieo được mặt 4.
Giải:
Số lần thực hiện thử nghiệm: 50
Số lần sự kiện “gieo được mặt 4” xảy ra: 10
Xác suất thực nghiệm để gieo được mặt 4: P(4) = 10 / 50 = 0.2
Xác suất thực nghiệm là một ước lượng của xác suất lý thuyết. Khi số lần thực hiện thử nghiệm càng lớn, xác suất thực nghiệm càng gần với xác suất lý thuyết. Ví dụ, khi gieo một đồng xu một số lượng lớn các lần, xác suất thực nghiệm của việc xuất hiện mặt ngửa sẽ tiến gần đến 0.5.
Hy vọng bài học này đã giúp các em hiểu rõ hơn về Lý thuyết Xác suất thực nghiệm Toán 6 KNTT với cuộc sống. Chúc các em học tập tốt!