Chào mừng các em học sinh đến với bài học về Lý thuyết Thứ tự thực hiện các phép tính Toán 6 KNTT với cuộc sống. Bài học này sẽ giúp các em nắm vững quy tắc quan trọng trong toán học, áp dụng vào giải quyết các bài toán thực tế.
Chúng ta sẽ cùng nhau tìm hiểu về thứ tự ưu tiên của các phép tính, cách sử dụng dấu ngoặc để thay đổi thứ tự thực hiện, và những lưu ý quan trọng để tránh sai sót trong quá trình tính toán.
Lý thuyết Thứ tự thực hiện các phép tính Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu
1. Nhắc lại kiến thức cũ
Các số được nối với nhau bởi dấu các phép tính (cộng, trừ, nhân chia, nâng lên lũy thừa) làm thành một biểu thức.
Trong một biểu thức có thể có dấu ngoặc.
2. Quy ước thực hiện các phép tính
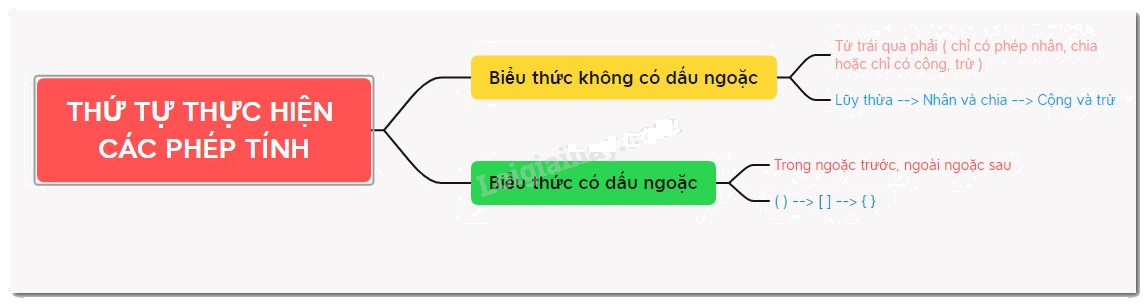
a. Đối với biểu thức không có dấu ngoặc.
+ Nếu phép tính chỉ có cộng, trừ hoặc chỉ có nhân, chia, ta thực hiện phép tính theo thứ tự từ trái sang phải.
+ Nếu phép tính có cả cộng , trừ, nhân, chia, nâng lên lũy thừa, ta thực hiện phép nâng lên lũy thừa trước, rồi đến nhân chia, cuối cùng đến cộng trừ.
Lũy thừa \( \to \) nhân và chia \( \to \) cộng và trừ.
b. Đối với biểu thức có dấu ngoặc.
Nếu biểu thức có các dấu ngoặc : ngoặc tròn ( ), ngoặc vuông [ ], ngoặc nhọn { }, ta thực hiện phép tính theo thứ tự : \(\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}\)
Ví dụ:
Tính giá trị của các biểu thức sau:
a) \(3 + 2.5\)
Trong biểu thức có phép cộng và phép nhân nên ta thực hiện phép nhân trước, tính 2.5 trước rồi cộng với 3.
Ta có: \(3 + 2.5 = 3 + 10 = 13\)
b) \(5.\left( {{3^2} - 2} \right)\)
Trong biểu thức có dấu ngoặc nên ta thực hiện phép tính trong ngoặc trước rồi nhân với 5 sau:
Trong ngoặc có phép nâng lên lũy thừa nên ta tính \({3^2}\) trước rồi trừ đi 2.
\(\left( {{3^2} - 2} \right) = \left( {9 - 2} \right) = 7\)
\(5.\left( {{3^2} - 2} \right) = 5.\left( {9 - 2} \right) = 5.7 = 35\)
Trong toán học, thứ tự thực hiện các phép tính là một quy tắc quan trọng giúp đảm bảo tính chính xác của kết quả. Quy tắc này được gọi là quy tắc BODMAS/PEMDAS, và nó quy định thứ tự ưu tiên của các phép tính như sau:
1. Dấu Ngoặc:
Dấu ngoặc có vai trò quan trọng nhất trong việc thay đổi thứ tự thực hiện các phép tính. Các phép tính trong dấu ngoặc phải được thực hiện trước, từ trong ra ngoài.
Ví dụ:
2 + (3 x 4) = 2 + 12 = 14
(2 + 3) x 4 = 5 x 4 = 20
2. Lũy Thừa và Căn Bậc Hai:
Sau dấu ngoặc, các phép tính lũy thừa và căn bậc hai được thực hiện trước.
Ví dụ:
23 + 5 = 8 + 5 = 13
√9 - 2 = 3 - 2 = 1
3. Phép Nhân và Phép Chia:
Phép nhân và phép chia có cùng mức độ ưu tiên, và được thực hiện từ trái sang phải.
Ví dụ:
10 x 2 : 5 = 20 : 5 = 4
15 : 3 x 2 = 5 x 2 = 10
4. Phép Cộng và Phép Trừ:
Phép cộng và phép trừ có cùng mức độ ưu tiên, và được thực hiện từ trái sang phải.
Ví dụ:
8 - 3 + 2 = 5 + 2 = 7
4 + 5 - 1 = 9 - 1 = 8
Áp Dụng Vào Cuộc Sống:
Thứ tự thực hiện các phép tính không chỉ quan trọng trong toán học mà còn ứng dụng trong nhiều tình huống thực tế. Ví dụ:
Bài Tập Thực Hành:
Để củng cố kiến thức về thứ tự thực hiện các phép tính, hãy cùng làm một số bài tập sau:
Lưu Ý Quan Trọng:
Hy vọng bài học này đã giúp các em hiểu rõ hơn về Lý thuyết Thứ tự thực hiện các phép tính Toán 6 KNTT với cuộc sống. Chúc các em học tập tốt!