Chào mừng các em học sinh đến với bài học về Lý thuyết Tính toán với số thập phân trong chương trình Toán 6 KNTT. Bài học này sẽ giúp các em hiểu rõ hơn về khái niệm số thập phân, cách so sánh, cộng, trừ, nhân, chia các số thập phân và ứng dụng của chúng trong cuộc sống hàng ngày.
Giaitoan.edu.vn cung cấp kiến thức toán học một cách dễ hiểu, trực quan, giúp các em học tập hiệu quả và đạt kết quả tốt nhất.
Lý thuyết Tính toán với số thập phân Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu
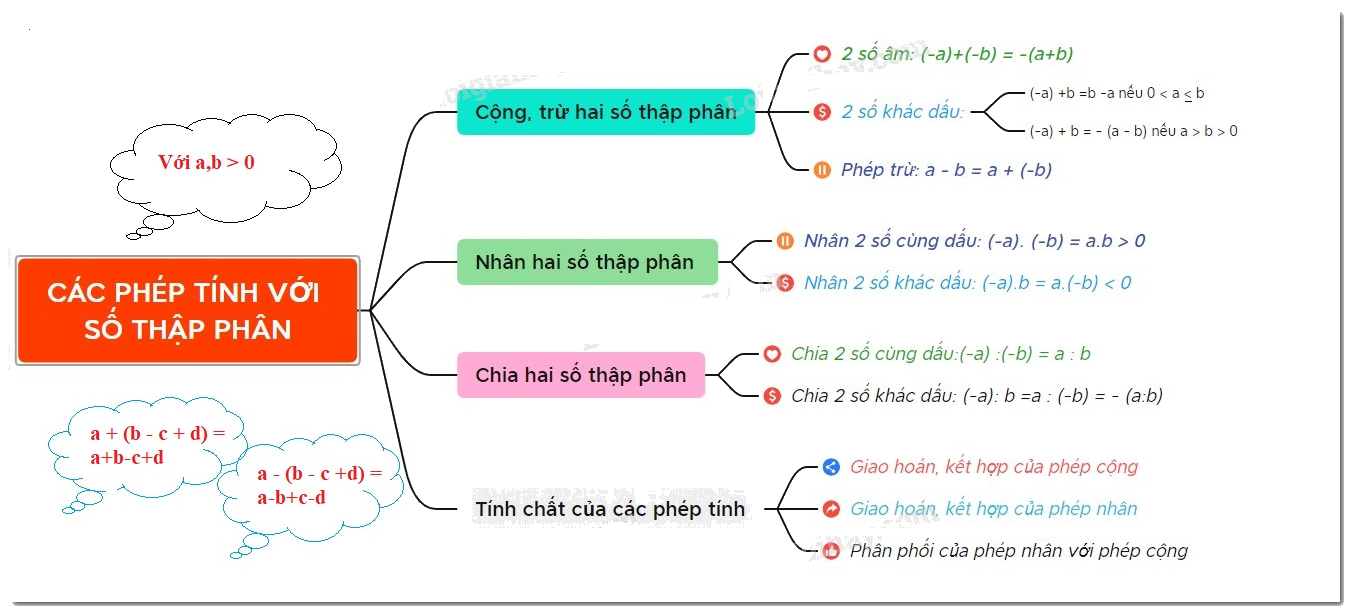
1. Cộng, trừ hai số thập phân
Số đối của số thập phân a kí hiệu là -a. Ta có: a +(-a)=0
Để thực hiện cộng trừ các phép tính cộng và trừ các số thập phân, ta áp dụng các quy tắc dấu như khi thực hiện các phép tính cộng và trừ các số nguyên.
• Muốn cộng hai số thập phân âm, ta cộng hai số đối của chúng rồi thêm dấu trừ đằng trước kết quả.
• Muốn cộng hai số thập phân trái dấu, ta làm như sau:
◊ Nếu số dương lớn hơn hay bằng số đối của số âm thì ta lấy số dương trừ đi số đối của số âm.
◊ Nếu số dương nhỏ hơn số đối của số âm thì ta lấy số đối của số âm trừ đi số dương rồi thêm dấu trừ (-) trước kết quả.
• Muốn trừ số thập phân a cho số thập phân b, ta cộng a với số đối của b.
Nhận xét:
• Tổng của hai số thập phân cùng dấu luôn cùng dấu với hai số thập phân đó.
• Khi cộng hai số thập phân trái dấu:
◊ Nếu số dương lớn hơn số đối của số âm thì ta có tổng dương.
◊ Nếu số dương nhỏ hơn số đối của số âm thì ta có tổng âm trừ.
2. Phép nhân số thập phân
a)Nhân 2 số thập phân
Muốn nhân hai số thập phân dương có nhiều chữ số thập phân, ta làm như sau:
+Viết thừa số này dưới thừa số kia như đối với phép nhân các số tự nhiên
+Thực hiện nhân như nhân số tự nhiên
+Đếm xem trong phần thập phân ở cả hai thừa số có tất cả bao nhiêu chữ số rồi dùng dấu phẩu tách ở tích ra bấy nhiêu chữ số từ phải sang trái.
*2 số thập phân cùng dấu thì tích là số dương; 2 số thập phân khác dấu thì tích là số âm
3. Phép chia số thập phân
Muốn chia hai số thập phân dương có nhiều chữ số thập phân, ta làm như sau:
+Đếm xem có bao nhiêu chữ số ở phần thập phân của số chia thì chuyển dấu phẩy ở số bị chia sang bên phải bấy nhiêu chữ số.
Chú ý: Khi chuyển dấu phẩy ở số bị chia sang phải mà không đủ chữ số, ta thấy thiếu bao nhiêu chữ số thì thêm vào đó bấy nhiêu chữ số 0.
+Bỏ dấu phẩy ở số chia ta được số nguyên dương
+ Thực hiện phép chia như số thập phân cho số tự nhiên
Chú ý:
• Tích và thương của hai số thập phân cùng dấu luôn là một số dương.
• Tích và thương của hai số thập phân khác dấu luôn là một số âm.
• Khi nhân hoặc chia hai số thập phân cùng âm, ta nhân hoặc chia hai số đối của chúng.
• Khi nhân hoặc chia hai số thập phân khác dấu, ta chỉ thực hiện phép nhân hoặc chia giữa số dương và số đối của số âm rồi thêm dấu trừ (-) trước kết quả nhận được.
Quy tắc dấu ngoặc:
• Khi bỏ dấu ngoặc có dấu (+) đứng trước thì dấu các số hạng trong ngoặc vẫn giữ nguyên; Khi bỏ dấu ngoặc có dấu (-) đứng trước, ta phải đổi dấu tất cả các số hạng trong dấu ngoặc.
• Khi đưa nhiều số hạng vào trong dấu ngoặc và để dấu (-) đứng trước thì ta phải đổi dấu của tất cả các số hạng đó.
4. Tính giá trị biểu thức với số thập phân
Phép cộng và phép nhân số thập phân cũng có các tính chất giao hoán, kết hợp, phân phối như phép cộng, phép nhân của số nguyên và phân số. Vận dụng các tính chất này ta có thể tính giá trị các biểu thức một cách hợp lí
Số thập phân là một phần quan trọng trong chương trình Toán 6, là nền tảng cho các kiến thức toán học nâng cao hơn. Hiểu rõ về số thập phân giúp học sinh giải quyết các bài toán thực tế một cách dễ dàng và chính xác.
Số thập phân là cách biểu diễn các số không nguyên bằng cách sử dụng dấu phẩy (,) để phân tách phần nguyên và phần thập phân. Ví dụ: 3,5; 0,75; 12,01 là các số thập phân.
Để so sánh hai số thập phân, ta thực hiện theo các bước sau:
Ví dụ: 3,5 > 3,2; 0,75 < 0,8; 12,01 = 12,01
Để cộng hoặc trừ các số thập phân, ta thực hiện theo các bước sau:
Ví dụ:
| 3,5 | + 2,7 | ||
|---|---|---|---|
| 3,5 | 2,7 | ||
| 6,2 |
Để nhân hai số thập phân, ta thực hiện theo các bước sau:
Ví dụ: 3,5 x 2,7 = 9,45
Để chia một số thập phân cho một số thập phân, ta thực hiện theo các bước sau:
Ví dụ: 9,45 : 2,7 = 3,5
Số thập phân được ứng dụng rộng rãi trong cuộc sống hàng ngày, ví dụ:
Hy vọng bài học này đã giúp các em hiểu rõ hơn về Lý thuyết Tính toán với số thập phân Toán 6 KNTT với cuộc sống. Chúc các em học tập tốt!