Bài học này sẽ giúp các em học sinh lớp 6 nắm vững kiến thức về lý thuyết thứ tự trong tập hợp các số tự nhiên, một nền tảng quan trọng trong chương trình Toán học. Chúng ta sẽ cùng nhau khám phá cách so sánh các số tự nhiên, xác định số lớn hơn, số nhỏ hơn và hiểu rõ ý nghĩa của thứ tự trên trục số.
Với phương pháp tiếp cận KNTT (Kết nối tri thức với cuộc sống), bài học không chỉ dừng lại ở việc học thuộc lòng công thức mà còn giúp các em hiểu được ứng dụng thực tế của kiến thức này trong đời sống hàng ngày.
Lý thuyết Thứ tự trong tập hợp các số tự nhiên Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu
1. Biểu diễn số tự nhiên trên tia số
Tập hợp các số tự nhiên kí hiệu là \(N\) , tập hợp các số tự nhiên khác 0 kí hiệu là \({N^*}\) .
Ta có:
N = { 0; 1; 2 ; 3 ; 4 ;......}
\({N^*}\)= {1 ; 2 ; 3 ; 4; ......}
Mỗi số tự nhiên được biểu diễn bởi một điểm trên tia số. Trên tia số, điểm biểu diễn số nhỏ ở bên trái điểm biểu diễn số lớn.
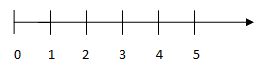
Số tự nhiên a được gọi là điểm a. Điểm 0 là gốc.
Ví dụ: Điểm biểu diễn số 4 trên tia số ta gọi là điểm 4.
2. Thứ tự trong tập hợp các số tự nhiên
+ Trong hai số tự nhiên khác nhau, có một số nhỏ hơn số kia, ta viết \(a < b\) hoặc \(b > a.\)
Ngoài ra ta cũng viết \(a \ge b\) để chỉ \(a > b\) hoặc \(a = b.\)
+ Nếu \(a < b\) và \(b < c\) thì \(a < c.\) (Tính chất bắc cầu)
+ Hai số tự nhiên liên tiếp hơn kém nhau 1 đơn vị. Mỗi số tự nhiên có một số liền sau duy nhất và một số liền trước duy nhất.
+ Số 0 là số tự nhiên bé nhất.
Ví dụ:
Số 3 và số 4 là hai số tự nhiên liên tiếp. Số liền sau của 8 là 9.
Số liền trước của 6 là 5.
Các dạng bài tập
1. Tìm số liền sau, số liền trước của một số tự nhiên cho trước
Phương pháp:
- Để tìm số liền sau của số tự nhiên $a,$ ta tính $a + 1.$
- Để tìm số liền trước của số tự nhiên $a$ khác $0,$ta tính $a - 1.$
Chú ý:
- Số $0$ không có số liền trước.
- Hai số tự nhiên liên tiếp thì hơn kém nhau $1$ đơn vị.
2. Tìm các số tự nhiên thỏa mãn điều kiện cho trước
Phương pháp:
Liệt kê tất cả các số tự nhiên thỏa mãn đồng thời các điều kiện đã cho
Ví dụ:
Tìm tất cả các số tự nhiên thỏa mãn \(12 < x < 16\)
Giải:
Ta có: các số tự nhiên lớn hơn $12$ và nhỏ hơn $16$ là: $13; 14; 15$.
Tìm tất cả các số tự nhiên thỏa mãn \(12 < x < 16\)
3. Sử dụng công thức đếm số các số tự nhiên
Phương pháp:
Để đếm các số tự nhiên từ $a$ đến $b,$ hai số liên tiếp cách nhau $d$ đơn vị, ta dùng công thức sau:
$\dfrac{{b - a}}{d} + 1$ hay bằng (số cuối – số đầu):khoảng cách +1.
- Căn cứ vào các phần tử đã được liệt kê hoặc căn cứ vào tính chất đặc trưng cho các phần tử của tập hợp cho trước, ta có thể tìm được số phần tử của tập hợp đó.
- Sử dụng các công thức sau:
+ Tập hợp các số tự nhiên từ $a$ đến $b$ có: $b-a + 1$ phần tử (1)
+ Tập hợp các số chẵn từ số chẵn $a$ đến số chẵn $b$ có: $\left( {b-a} \right):2 + 1$ phần tử ( 2)
+ Tập hợp các số lẻ từ số lẻ $m$ đến số lẻ $n$ có: $\left( {n - m} \right):2 + 1$ phần tử ( 3)
+ Tập hợp các số tự nhiên từ $a$ đến $b,$ hai số kế tiếp cách nhau d đơn vị, có: $\left( {b - a} \right):d + 1$ phần tử (4)
Trong chương trình Toán 6, việc làm quen với tập hợp số tự nhiên và các khái niệm liên quan đến thứ tự là vô cùng quan trọng. Nó không chỉ là nền tảng cho các kiến thức toán học nâng cao hơn mà còn giúp học sinh phát triển tư duy logic và khả năng giải quyết vấn đề.
Tập hợp số tự nhiên (N) bao gồm các số 0, 1, 2, 3,... được sử dụng để đếm và biểu thị số lượng. Việc hiểu rõ tập hợp này là bước đầu tiên để làm quen với các khái niệm về thứ tự.
Quan hệ thứ tự trên tập hợp số tự nhiên được biểu diễn bằng các ký hiệu: < (nhỏ hơn), > (lớn hơn), ≤ (nhỏ hơn hoặc bằng), ≥ (lớn hơn hoặc bằng), = (bằng). Để so sánh hai số tự nhiên, ta dựa vào số lượng đơn vị mà mỗi số đại diện.
Có hai cách chính để so sánh hai số tự nhiên:
Trục số là một công cụ trực quan giúp biểu diễn các số tự nhiên và quan hệ thứ tự giữa chúng. Trên trục số, các số tự nhiên được sắp xếp theo thứ tự tăng dần từ trái sang phải. Số nào nằm bên trái số khác thì nhỏ hơn, và ngược lại.
Lý thuyết thứ tự không chỉ dừng lại ở việc học trên lớp mà còn có nhiều ứng dụng thực tế trong cuộc sống:
Để củng cố kiến thức về lý thuyết thứ tự, chúng ta hãy cùng giải một số bài tập sau:
Ngoài lý thuyết thứ tự trong tập hợp số tự nhiên, các em có thể tìm hiểu thêm về:
Việc nắm vững kiến thức về các tập hợp số khác nhau sẽ giúp các em hiểu sâu hơn về Toán học và ứng dụng nó vào giải quyết các bài toán phức tạp hơn.
Lý thuyết thứ tự trong tập hợp số tự nhiên là một kiến thức cơ bản nhưng vô cùng quan trọng trong chương trình Toán 6. Hy vọng rằng, qua bài học này, các em đã nắm vững kiến thức và có thể vận dụng nó vào giải quyết các bài toán thực tế một cách hiệu quả.