Chào mừng các em học sinh đến với bài học về Lý thuyết Đoạn thẳng và Độ dài đoạn thẳng trong chương trình Toán 6 KNTT. Bài học này sẽ giúp các em hiểu rõ khái niệm đoạn thẳng, cách đo độ dài đoạn thẳng và ứng dụng của chúng trong thực tế.
Chúng ta sẽ cùng nhau khám phá những kiến thức cơ bản, thông qua các ví dụ minh họa sinh động và bài tập thực hành thú vị. Mục tiêu là giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán liên quan.
Lý thuyết Đoạn thẳng. Độ dài đoạn thẳng Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu
1. Hai đoạn thẳng bằng nhau
Đoạn thẳng AB là hình gồm hai điểm A, B và tất cả các điểm nằm giữa giữa A và B.
Đoạn thẳng AB còn gọi là đoạn thẳng BA.
Hai điểm A, B gọi là hai đầu mút (hoặc hai mút) của đoạn thẳng AB.
2. Độ dài đoạn thẳng
- Mỗi đoạn thẳng có một độ dài. Độ dài đoạn thẳng là một số dương.
- Độ dài đoạn thẳng AB là khoảng cách giữa hai điểm A và B.
- Nếu hai điểm trùng nhau thì khoảng cách giữa chúng bằng O.
Ví dụ: Đoạn thẳng CD dài 4 cm
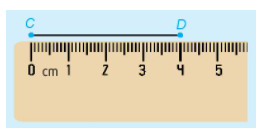
*So sánh hai đoạn thẳng
Ta so sánh hai đoạn thẳng bằng cách so sánh độ dài của chúng.
+ Ta có thể dùng mệnh đề: “Nếu \(AM + MB \ne AB\) thì điểm \(M\) không nằm giữa \(A\) và \(B.\)”
+ Nếu điểm \(M\) nằm giữa \(A\) và \(B;\) điểm \(N\) nằm giữa \(M\) và \(B\) thì \(AM + MN + NB = AB.\)
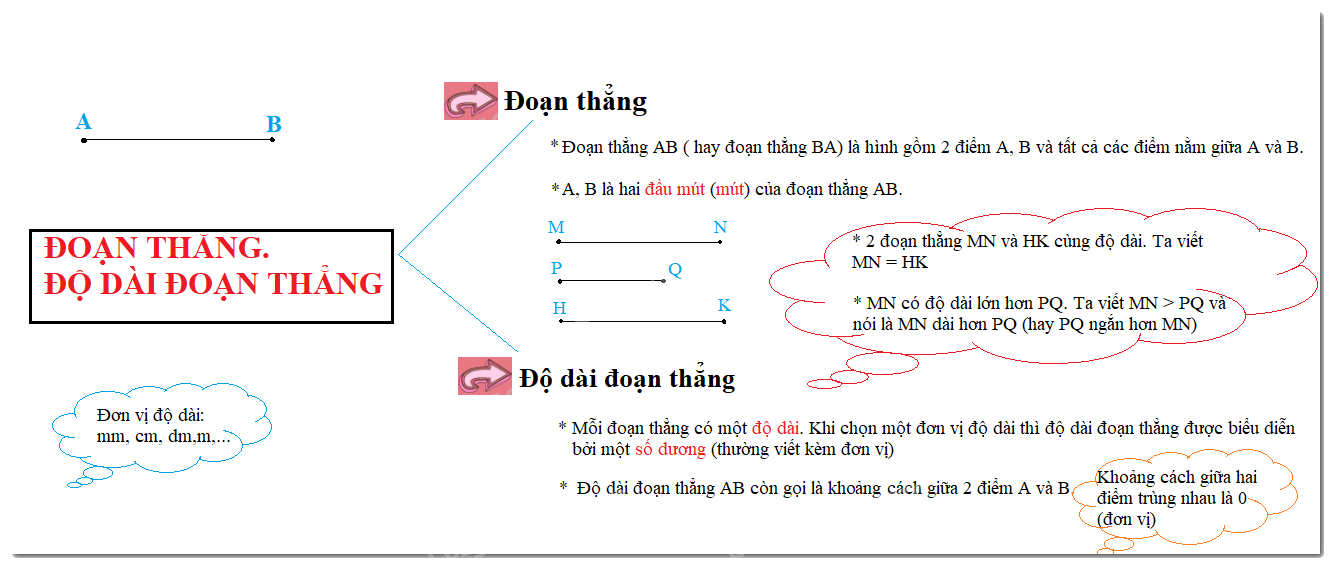
Trung điểm của đoạn thẳng là điểm nằm giữa và cách đều hai đầu đoạn thẳng. Trung điểm của đoạn thẳng còn gọi là điểm chính giữa của đoạn thẳng.
Tóm tắt:
\(I\) là trung điểm của đoạn thẳng \(AB\)$ \Leftrightarrow $${\rm{IA = IB}}$ và \(I\) nằm giữa hai điểm \(A;B.\)
hoặc \(I\) là trung điểm của đoạn thẳng \(AB\)$ \Leftrightarrow \left\{ \begin{array}{l}AI + IB = AB\\{\rm{IA = IB}}\end{array} \right.$
hoặc \(I\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AI = BI = }}\dfrac{1}{2}AB$

Giả sử ta cần vẽ trung điểm M của đoạn thẳng AB có độ dài 5 cm.
Cách 1:
- Đặt mép thước trung với đoạn thẳng AB sao cho vạch 0 trùng với điểm A, khi đó điểm B trùng với vạch chỉ số 5 trên thước.
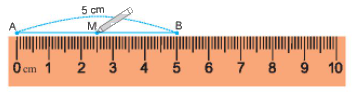
- Ta lấy điểm M trùng với vạch chỉ số 2,5 cm trên thước, Khi đó ta có M là trung điểm của đoạn thẳng AB.
Cách 2:
Vẽ đoạn thẳng AB trên giấy can. Gấp giấy sao cho điểm B trùng với điểm A. Giao của nếp gấp và đoạn thẳng AB chính là trung điểm M cần xác định
Trung điểm của đoạn thẳng là điểm nằm giữa và cách đều hai đầu đoạn thẳng. Trung điểm của đoạn thẳng còn gọi là điểm chính giữa của đoạn thẳng.
Tóm tắt:
\(I\) là trung điểm của đoạn thẳng \(AB\)$ \Leftrightarrow $${\rm{IA = IB}}$ và \(I\) nằm giữa hai điểm \(A;B.\)
hoặc \(I\) là trung điểm của đoạn thẳng \(AB\)$ \Leftrightarrow \left\{ \begin{array}{l}AI + IB = AB\\{\rm{IA = IB}}\end{array} \right.$
hoặc \(I\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AI = BI = }}\dfrac{1}{2}AB$

Giả sử ta cần vẽ trung điểm M của đoạn thẳng AB có độ dài 5 cm.
Cách 1:
- Đặt mép thước trung với đoạn thẳng AB sao cho vạch 0 trùng với điểm A, khi đó điểm B trùng với vạch chỉ số 5 trên thước.
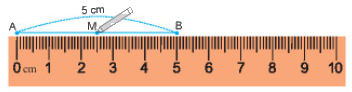
- Ta lấy điểm M trùng với vạch chỉ số 2,5 cm trên thước, Khi đó ta có M là trung điểm của đoạn thẳng AB.
Cách 2:
Vẽ đoạn thẳng AB trên giấy can. Gấp giấy sao cho điểm B trùng với điểm A. Giao của nếp gấp và đoạn thẳng AB chính là trung điểm M cần xác định
Trong chương trình Toán 6 KNTT, kiến thức về đoạn thẳng và độ dài đoạn thẳng là nền tảng quan trọng để xây dựng các khái niệm hình học phức tạp hơn. Bài viết này sẽ cung cấp một cái nhìn toàn diện về chủ đề này, từ định nghĩa cơ bản đến các ứng dụng thực tế.
Định nghĩa: Đoạn thẳng là hình gồm hai điểm và tất cả các điểm nằm giữa hai điểm đó. Hai điểm đó gọi là hai mút của đoạn thẳng.
Ký hiệu: AB là đoạn thẳng có hai mút là A và B.
Ví dụ: Trên hình vẽ, đoạn thẳng MN gồm hai mút M và N, và tất cả các điểm nằm trên đường thẳng MN giữa M và N đều thuộc đoạn thẳng MN.
Định nghĩa: Độ dài của đoạn thẳng là khoảng cách giữa hai mút của đoạn thẳng đó.
Đơn vị đo: Độ dài đoạn thẳng thường được đo bằng các đơn vị như centimet (cm), mét (m), milimet (mm),...
Cách đo: Để đo độ dài đoạn thẳng, ta sử dụng thước đo. Đặt thước sao cho một đầu của thước trùng với một mút của đoạn thẳng, sau đó đọc số đo ở mút còn lại.
Để so sánh độ dài hai đoạn thẳng, ta thực hiện đo độ dài của mỗi đoạn thẳng, sau đó so sánh các số đo đó.
Định nghĩa: Trung điểm M của đoạn thẳng AB là điểm nằm giữa A và B sao cho AM = MB.
Cách tìm trung điểm: Để tìm trung điểm của đoạn thẳng AB, ta đo độ dài của đoạn thẳng AB, sau đó chia độ dài đó cho 2. Điểm cách A một khoảng bằng kết quả vừa tìm được là trung điểm của đoạn thẳng AB.
Kiến thức về đoạn thẳng và độ dài đoạn thẳng có rất nhiều ứng dụng trong cuộc sống hàng ngày:
Bài 1: Vẽ đoạn thẳng CD có độ dài 5cm. Xác định trung điểm M của đoạn thẳng CD.
Bài 2: So sánh độ dài của hai đoạn thẳng AB = 8cm và MN = 6cm.
Bài 3: Một đoạn thẳng PQ có độ dài 12cm. Điểm I nằm giữa P và Q sao cho PI = 4cm. Tính độ dài đoạn thẳng IQ.
Bài học về Lý thuyết Đoạn thẳng và Độ dài đoạn thẳng Toán 6 KNTT đã cung cấp cho các em những kiến thức cơ bản và quan trọng. Việc nắm vững kiến thức này sẽ giúp các em học tốt môn Toán và ứng dụng vào thực tế một cách hiệu quả. Hãy luyện tập thường xuyên để củng cố kiến thức và tự tin giải quyết các bài toán liên quan.