Chào mừng các em học sinh đến với bài học về Lý thuyết Trung điểm của đoạn thẳng trong chương trình Toán 6 KNTT. Bài học này sẽ giúp các em hiểu rõ khái niệm trung điểm, cách xác định trung điểm của một đoạn thẳng và ứng dụng của lý thuyết này vào giải các bài toán thực tế.
Chúng ta sẽ cùng nhau khám phá những kiến thức cơ bản, thông qua các ví dụ minh họa sinh động và bài tập vận dụng đa dạng. Mục tiêu là giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán liên quan.
Lý thuyết Trung điểm của đoạn thẳng Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu
Trung điểm của đoạn thẳng là điểm nằm giữa và cách đều hai đầu đoạn thẳng. Trung điểm của đoạn thẳng còn gọi là điểm chính giữa của đoạn thẳng.
Tóm tắt:
\(I\) là trung điểm của đoạn thẳng \(AB\)$ \Leftrightarrow $${\rm{IA = IB}}$ và \(I\) nằm giữa hai điểm \(A;B.\)
hoặc \(I\) là trung điểm của đoạn thẳng \(AB\)$ \Leftrightarrow \left\{ \begin{array}{l}AI + IB = AB\\{\rm{IA = IB}}\end{array} \right.$
hoặc \(I\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AI = BI = }}\dfrac{1}{2}AB$
Giả sử ta cần vẽ trung điểm M của đoạn thẳng AB có độ dài 5 cm.
Cách 1:
- Đặt mép thước trung với đoạn thẳng AB sao cho vạch 0 trùng với điểm A, khi đó điểm B trùng với vạch chỉ số 5 trên thước.
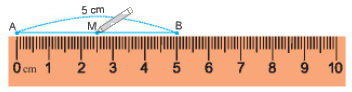
- Ta lấy điểm M trùng với vạch chỉ số 2,5 cm trên thước, Khi đó ta có M là trung điểm của đoạn thẳng AB.
Cách 2:
Vẽ đoạn thẳng AB trên giấy can. Gấp giấy sao cho điểm B trùng với điểm A. Giao của nếp gấp và đoạn thẳng AB chính là trung điểm M cần xác định

Trong chương trình Toán 6 KNTT, khái niệm trung điểm của đoạn thẳng là một kiến thức nền tảng quan trọng. Nó không chỉ xuất hiện trong các bài toán hình học cơ bản mà còn có ứng dụng thực tế trong nhiều lĩnh vực khác nhau. Bài viết này sẽ cung cấp một cách đầy đủ và dễ hiểu về lý thuyết này, giúp các em học sinh nắm vững kiến thức và tự tin áp dụng vào giải bài tập.
Một điểm được gọi là trung điểm của đoạn thẳng nếu nó nằm trên đoạn thẳng đó và cách đều hai mút của đoạn thẳng. Nói cách khác, nếu M là trung điểm của đoạn thẳng AB, thì AM = MB.
Có nhiều cách để xác định trung điểm của một đoạn thẳng:
M( (xA + xB)/2 ; (yA + yB)/2 )
Lý thuyết trung điểm của đoạn thẳng có rất nhiều ứng dụng trong thực tế:
Bài 1: Cho đoạn thẳng AB dài 8cm. Gọi M là trung điểm của đoạn thẳng AB. Tính độ dài đoạn thẳng AM và MB.
Giải: Vì M là trung điểm của đoạn thẳng AB, nên AM = MB = AB/2 = 8cm/2 = 4cm.
Bài 2: Cho A(1, 2) và B(5, 6). Tìm tọa độ trung điểm M của đoạn thẳng AB.
Giải: Tọa độ trung điểm M của đoạn thẳng AB là:
M( (1 + 5)/2 ; (2 + 6)/2 ) = M(3; 4)
Khái niệm trung điểm không chỉ giới hạn trong hình học mà còn xuất hiện trong nhiều lĩnh vực khác của cuộc sống. Ví dụ, trong việc chia sẻ tài sản, việc tìm ra điểm trung hòa giữa các bên liên quan là rất quan trọng. Hay trong việc thiết kế nội thất, việc bố trí các đồ vật sao cho cân đối và hài hòa cũng dựa trên nguyên tắc tìm điểm trung tâm.
Lý thuyết Trung điểm của đoạn thẳng Toán 6 KNTT là một kiến thức cơ bản nhưng vô cùng quan trọng. Việc nắm vững lý thuyết này sẽ giúp các em học sinh giải quyết các bài toán hình học một cách dễ dàng và tự tin hơn. Hy vọng bài viết này đã cung cấp cho các em những kiến thức hữu ích và thú vị về chủ đề này.