Lý thuyết Hình có trục đối xứng Toán 6 KNTT với cuộc sống

Chào mừng bạn đến với bài học về Lý thuyết Hình có trục đối xứng trong chương trình Toán 6 KNTT. Bài học này sẽ giúp bạn hiểu rõ khái niệm, tính chất của trục đối xứng và cách nhận biết các hình có trục đối xứng.

Chúng ta sẽ cùng nhau khám phá những ứng dụng thú vị của kiến thức này trong cuộc sống hàng ngày, từ những vật dụng quen thuộc đến các công trình kiến trúc.

Lý thuyết Hình có trục đối xứng Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu

1. Hình có trục đối xứng trong thực tế

Có một đường thẳng d chia hình thành hai phần mà khi ta “gấp” hình theo đường thẳng d thì hai phần đó “chồng khít” lên nhau.

Những hình như thế là hình có trục đối xứng và đường thẳng d là trục đối xứng của nó.

Ví dụ:

Lý thuyết Hình có trục đối xứng Toán 6 KNTT với cuộc sống 1

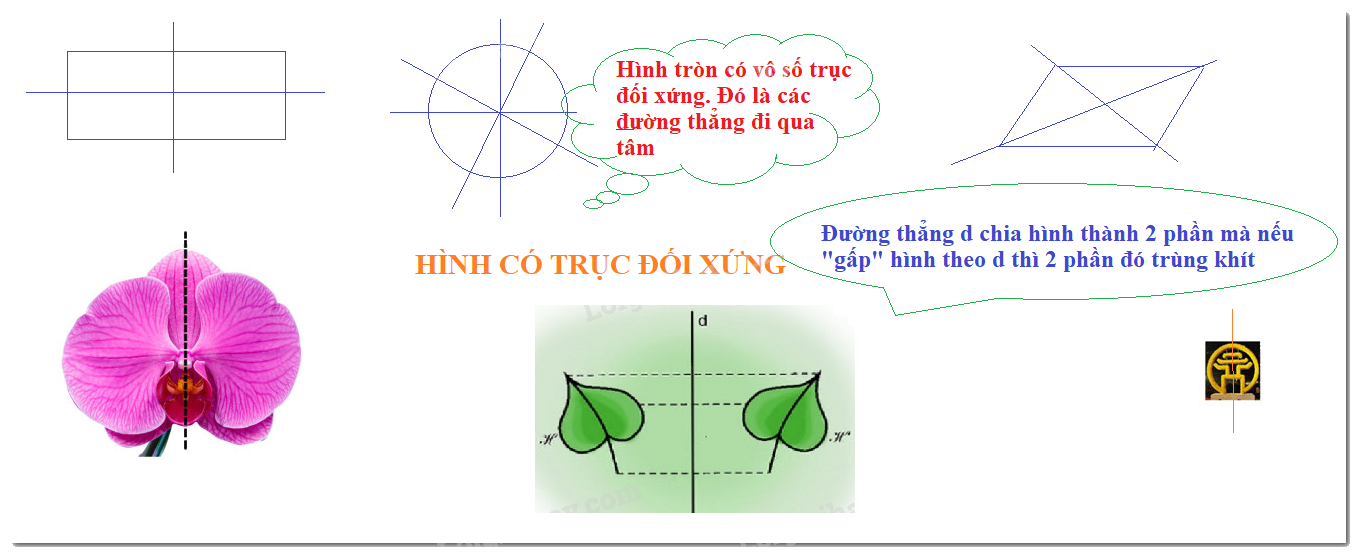
2. Trục đối xứng của một số hình phẳng

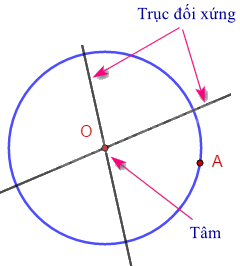
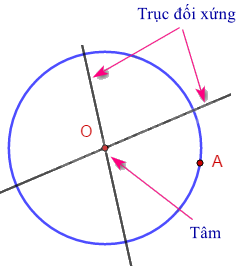
- Đường tròn: Mỗi đường thăng đi qua tâm là một trục đối xứng.

Lý thuyết Hình có trục đối xứng Toán 6 KNTT với cuộc sống 2

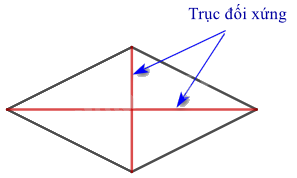
- Hình thoi: Mỗi đường chéo là một trục đối xứng.

Lý thuyết Hình có trục đối xứng Toán 6 KNTT với cuộc sống 3

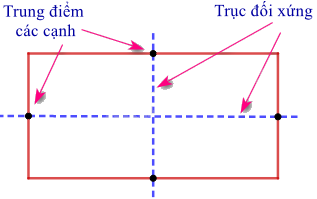
- Hình chữ nhật: Mỗi đường thẳng đi qua trung điểm hai cạnh đối diện là một trục đối xứng của hình chữ nhật.

Lý thuyết Hình có trục đối xứng Toán 6 KNTT với cuộc sống 4

Ứng dụng tính đối xứng để cắt chữ bằng giấy:

Bước 1: Gấp đôi mảnh giấy chữ nhật có kích thước 3 cm x 5 cm theo đường nét đứt (trục đối xứng) như hình:

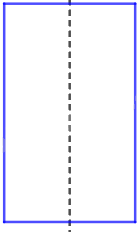
Lý thuyết Hình có trục đối xứng Toán 6 KNTT với cuộc sống 5

Bước 2: Vẽ một nửa chữ có trục đối xứng rồi cắt theo các nét vẽ mà ta đã vẽ xong. (Cắt theo đường màu đỏ giống như hình.

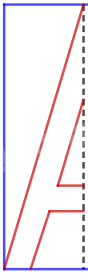
Lý thuyết Hình có trục đối xứng Toán 6 KNTT với cuộc sống 6

Lý thuyết Hình có trục đối xứng Toán 6 KNTT với cuộc sống 7

Tự tin bứt phá năm học lớp 6 ngay từ đầu! Khám phá Lý thuyết Hình có trục đối xứng Toán 6 KNTT với cuộc sống – nội dung then chốt trong chuyên mục giải toán 6 trên nền tảng toán. Với bộ bài tập toán thcs được biên soạn chuyên sâu, cập nhật chính xác theo khung chương trình sách giáo khoa THCS, đây chính là người bạn đồng hành đáng tin cậy giúp các em tối ưu hóa toàn diện quá trình ôn luyện và xây dựng nền tảng kiến thức Toán vững chắc thông qua phương pháp tiếp cận trực quan, mang lại hiệu quả vượt trội không ngờ.

Lý thuyết Hình có trục đối xứng Toán 6 KNTT với cuộc sống

Trong chương trình Toán 6 KNTT, kiến thức về hình học đóng vai trò quan trọng trong việc phát triển tư duy không gian và khả năng quan sát của học sinh. Một trong những khái niệm cơ bản và thú vị nhất là Lý thuyết Hình có trục đối xứng. Bài viết này sẽ cung cấp một cái nhìn toàn diện về chủ đề này, từ định nghĩa, tính chất đến các ứng dụng thực tế.

1. Định nghĩa Hình có trục đối xứng

Một hình được gọi là có trục đối xứng nếu có một đường thẳng (gọi là trục đối xứng) sao cho khi gấp hình theo đường thẳng đó, hai phần của hình trùng khít lên nhau. Nói cách khác, hình có trục đối xứng là hình có tính đối xứng qua một đường thẳng.

2. Tính chất của Trục đối xứng

Trục đối xứng là đường thẳng chia hình thành hai phần bằng nhau.
Mỗi điểm trên hình có một điểm đối xứng qua trục đối xứng.
Khoảng cách từ một điểm trên hình đến trục đối xứng bằng khoảng cách từ điểm đối xứng của nó đến trục đối xứng.

3. Các hình có trục đối xứng thường gặp

Có rất nhiều hình trong thực tế có trục đối xứng. Dưới đây là một số ví dụ điển hình:

Hình vuông: Có 4 trục đối xứng (hai đường thẳng nối trung điểm các cạnh đối diện và hai đường chéo).
Hình chữ nhật: Có 2 trục đối xứng (hai đường thẳng nối trung điểm các cạnh đối diện).
Hình thoi: Có 2 trục đối xứng (hai đường chéo).
Hình tròn: Có vô số trục đối xứng (mọi đường thẳng đi qua tâm của hình tròn đều là trục đối xứng).
Tam giác cân: Có 1 trục đối xứng (đường cao hạ từ đỉnh cân xuống cạnh đáy).
Tam giác đều: Có 3 trục đối xứng (ba đường cao).

4. Cách nhận biết Hình có trục đối xứng

Để nhận biết một hình có trục đối xứng hay không, bạn có thể thực hiện các bước sau:

Vẽ một đường thẳng bất kỳ qua hình.
Gấp hình theo đường thẳng đó.
Nếu hai phần của hình trùng khít lên nhau, thì đường thẳng đó là trục đối xứng của hình.

5. Ứng dụng của Lý thuyết Hình có trục đối xứng trong cuộc sống

Lý thuyết Hình có trục đối xứng không chỉ là kiến thức lý thuyết mà còn có rất nhiều ứng dụng thực tế trong cuộc sống:

Kiến trúc: Nhiều công trình kiến trúc được thiết kế dựa trên nguyên tắc đối xứng để tạo ra sự cân bằng và hài hòa. Ví dụ: các đền thờ, cung điện, nhà hát...
Thiết kế: Trong thiết kế đồ họa, thời trang, nội thất, yếu tố đối xứng được sử dụng để tạo ra các sản phẩm đẹp mắt và thu hút.
Nghệ thuật: Các tác phẩm nghệ thuật thường sử dụng đối xứng để tạo ra sự cân bằng và hài hòa trong bố cục.
Tự nhiên: Trong tự nhiên, chúng ta cũng bắt gặp nhiều hình ảnh đối xứng, ví dụ: cơ thể con người, lá cây, cánh bướm...

6. Bài tập vận dụng

Để củng cố kiến thức về Lý thuyết Hình có trục đối xứng, bạn có thể thực hiện các bài tập sau:

Vẽ các hình có trục đối xứng khác nhau.
Tìm trục đối xứng của các hình đã cho.
Nhận biết các hình có trục đối xứng trong thực tế.

7. Kết luận

Lý thuyết Hình có trục đối xứng là một khái niệm quan trọng trong chương trình Toán 6 KNTT. Việc nắm vững kiến thức này không chỉ giúp bạn giải quyết các bài toán hình học mà còn mở rộng khả năng quan sát và tư duy không gian. Hy vọng bài viết này đã cung cấp cho bạn những thông tin hữu ích và thú vị về chủ đề này.