Chương IV trong chương trình Toán học thường tập trung vào một chủ đề quan trọng, đòi hỏi sự nắm vững kiến thức nền tảng. Tại giaitoan.edu.vn, chúng tôi cung cấp hệ thống lý thuyết ôn tập chương IV được trình bày một cách rõ ràng, dễ hiểu.
Mục tiêu của chúng tôi là giúp bạn không chỉ hiểu bản chất của các khái niệm mà còn biết cách áp dụng chúng vào giải quyết các bài tập thực tế.
Lý thuyết ôn tập chương IV
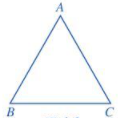
Tam giác đều \(ABC\) có:
+ Ba cạnh bằng nhau: \(AB = BC = CA\).
+ Ba góc ở các đỉnh \(A,B,\,C\) bằng nhau.
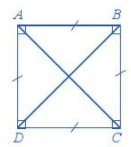
Bốn cạnh bằng nhau: \(AB = BC = CD = DA; \)
Hai cạnh đối \(AB \) và \(CD; \) \(AD \) và \(BC \) song song với nhau;
Hai đường chéo bằng nhau: \(AC = BD; \)
Bốn góc ở các đỉnh \(A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D \) là góc vuông.
Chu vi hình vuông cạnh a là: \(C = 4a\)
Diện tích hình vuông cạnh a là: \(S = a.a = {a^2}\).
Hình bình hành ABCD có:
- Bốn đỉnh A, B, C, D.
- Hai cặp cạnh đối diện bằng nhau: \(AB = CD;\,BC = AD\).
- Hai cặp cạnh đối diện song song: \(AB\) song song với \(CD\); \(BC\) song song với \(AD\).
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
- Hai góc ở các đỉnh A và C bằng nhau; hai góc ở các đỉnh B và D bằng nhau.
Chu vi hình bình hành : \(C = 2(a + b)\).
Diện tích hình bình hành là: \(S = b.h\)
Trong đó \(b\) là cạnh, \(h\) là chiều cao tương ứng.
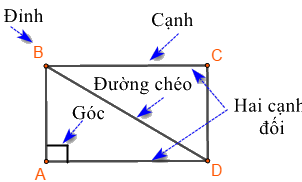
Hình chữ nhật \(ABCD\) có:
- Bốn đỉnh A, B, C, D
- Hai cặp cạnh đối diện bằng nhau: \(AB = CD;\,\,BC = AD\).
- Hai cặp cạnh đối diện song song: AB song song với CD; BC song song với AD.
- Bốn góc ở đỉnh A, B, C, D bằng nhau và bằng góc vuông.
- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường
Chu vi của hình chữ nhật là: \(C = 2\left( {a + b} \right);\)
Diện tích của hình chữ nhật là: \(S = a.b\)
Trong đó a, b là chiều dài và chiều rộng của hình chữ nhật.
V. Hình thoi
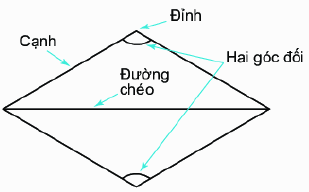
Hình thoi ABCD có:
- Bốn đỉnh A, B, C, D.
- Bốn cạnh bằng nhau:
- Hai cạnh đối AB và CD, AD và BC song song với nhau.
- Hai đường chéo AC và BD vuông góc với nhau.
Chu vi hình thoi cạnh a bằng độ dài cạnh nhân với bốn: \(C = 4a\)
Diện tích hình thoi cạnh a bằng nửa tích hai đường chéo: \(S = \frac{{m.n}}{2}\)
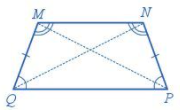
Hình thang cân \(MNPQ\) có:
Hai cạnh cạnh bên song song: \(MN\) song song với \(PQ\).
- Hai cạnh bên bằng nhau: \(MQ = NP\).
- Hai đường chéo bằng nhau: \(MP = NQ\).
- Hai góc kề với cạnh cạnh bên \(PQ\) bằng nhau.
- Chu vi của hình thang bằng tổng độ dài các cạnh của hình thang đó.
- Diện tích của hình thang bằng tổng độ dài hai đáy nhân với chiều cao rồi chia đôi.
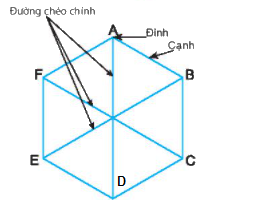
Lục giác đều \(ABCDEF\) có:
- Sáu đỉnh A, B, C, D, E, F
- Sáu cạnh bằng nhau: \(AB = BC = CD = DE = EF\).
- Sáu góc ở các đỉnh A, B, C, D, E, F bằng nhau.
- Ba đường chéo chính bằng nhau \(AD = BE = CF\).
Chương IV trong chương trình Toán học thường là một bước ngoặt quan trọng, nơi các khái niệm nền tảng được mở rộng và áp dụng vào các bài toán phức tạp hơn. Việc nắm vững lý thuyết chương IV là điều kiện tiên quyết để đạt kết quả tốt trong các kỳ thi và xây dựng nền tảng vững chắc cho các chương trình học nâng cao.
Tùy thuộc vào chương trình học cụ thể (Toán lớp 10, 11, 12), chương IV có thể bao gồm các chủ đề khác nhau. Tuy nhiên, một số chủ đề thường gặp bao gồm:
Để hiểu sâu sắc chương IV, bạn cần nắm vững các khái niệm cốt lõi sau:
Để ôn tập chương IV một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:
Lý thuyết chương IV có nhiều ứng dụng trong thực tế, bao gồm:
Chương IV thường xuất hiện các dạng bài tập sau:
Hy vọng rằng những thông tin trên sẽ giúp bạn ôn tập chương IV một cách hiệu quả và đạt kết quả tốt nhất. Hãy truy cập giaitoan.edu.vn để tìm hiểu thêm về các bài giảng và tài liệu ôn tập toán học.