Bài học này cung cấp kiến thức nền tảng về chu vi và diện tích của các tứ giác thường gặp trong chương trình Toán 6 KNTT. Chúng ta sẽ cùng nhau khám phá công thức tính chu vi và diện tích của hình vuông, hình chữ nhật, hình bình hành và hình thang.
Nội dung được trình bày một cách dễ hiểu, kết hợp với các ví dụ minh họa thực tế, giúp học sinh nắm vững lý thuyết và áp dụng vào giải bài tập một cách hiệu quả.
Lý thuyết Chu vi và diện tích của một số tứ giác đã học Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu
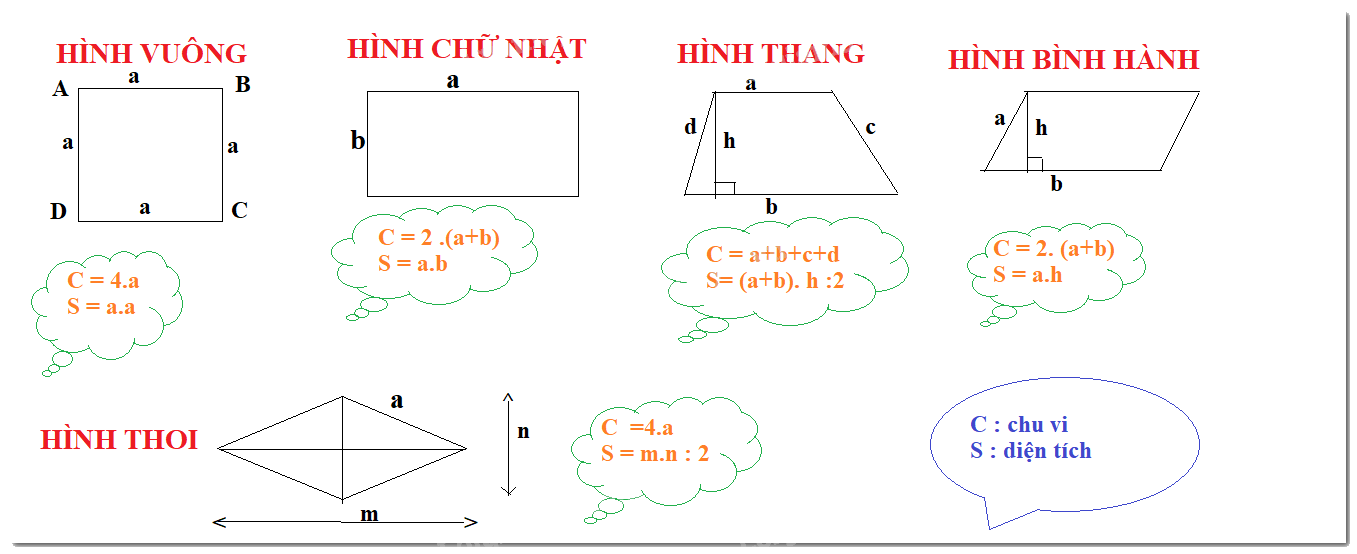
1. Chu vi, diện tích của hình vuông, hình chữ nhật, hình thang cân
Nhắc lại kiến thức
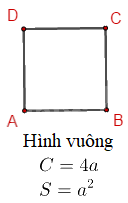
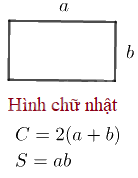
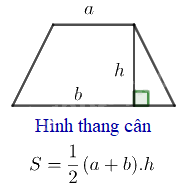(C là chu vi và S là diện tích)
2. Chu vi, diện tích của hình bình hành, hình thoi
Hình bình hành:
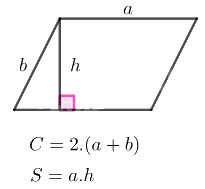
Với C là chu vi và S là diện tích
Hình thoi:
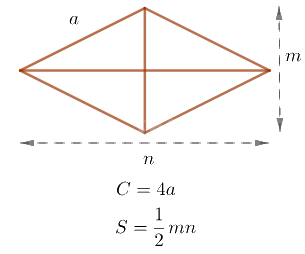
Với C là chu vi và S là diện tích
Trong chương trình Toán 6 KNTT, việc nắm vững kiến thức về chu vi và diện tích của các tứ giác là vô cùng quan trọng. Những kiến thức này không chỉ giúp học sinh giải quyết các bài toán trong sách giáo khoa mà còn ứng dụng vào thực tế cuộc sống hàng ngày.
Tứ giác là hình có bốn cạnh và bốn góc. Có rất nhiều loại tứ giác khác nhau, mỗi loại có những đặc điểm riêng. Trong chương trình Toán 6 KNTT, chúng ta sẽ tập trung vào bốn loại tứ giác phổ biến nhất: hình vuông, hình chữ nhật, hình bình hành và hình thang.
Hình vuông là tứ giác có bốn cạnh bằng nhau và bốn góc vuông.
Ví dụ: Một mảnh đất hình vuông có cạnh dài 10m. Vậy chu vi của mảnh đất là 4 * 10 = 40m và diện tích của mảnh đất là 102 = 100m2.
Hình chữ nhật là tứ giác có bốn góc vuông và hai cặp cạnh đối diện bằng nhau.
Ví dụ: Một phòng học hình chữ nhật có chiều dài 8m và chiều rộng 6m. Vậy chu vi của phòng học là 2(8 + 6) = 28m và diện tích của phòng học là 8 * 6 = 48m2.
Hình bình hành là tứ giác có hai cặp cạnh đối diện song song.
Ví dụ: Một khu vườn hình bình hành có cạnh đáy 12m và chiều cao tương ứng 5m. Vậy chu vi của khu vườn là 2(12 + 8) = 40m (giả sử cạnh còn lại là 8m) và diện tích của khu vườn là 12 * 5 = 60m2.
Hình thang là tứ giác có hai cạnh đối diện song song.
Ví dụ: Một mặt bàn hình thang có hai cạnh đáy lần lượt là 1.5m và 1m, chiều cao là 0.8m. Vậy chu vi của mặt bàn là 1.5 + 1 + 1.2 + 1.2 = 4.9m (giả sử hai cạnh bên bằng nhau và có độ dài 1.2m) và diện tích của mặt bàn là (1.5 + 1) * 0.8 / 2 = 1.4m2.
Việc tính chu vi và diện tích của các tứ giác có rất nhiều ứng dụng trong cuộc sống:
Để củng cố kiến thức, các em hãy tự giải các bài tập sau:
Hy vọng bài học này đã giúp các em hiểu rõ hơn về lý thuyết chu vi và diện tích của một số tứ giác đã học trong chương trình Toán 6 KNTT. Chúc các em học tốt!
