Bài học về Lý thuyết Điểm nằm giữa hai điểm. Tia Toán 6 KNTT là nền tảng quan trọng trong chương trình Toán học lớp 6. Nắm vững lý thuyết này giúp học sinh hiểu rõ hơn về các khái niệm cơ bản về hình học, đặc biệt là các yếu tố liên quan đến điểm, đường thẳng và tia.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu cùng với các bài tập thực hành đa dạng để giúp học sinh nắm vững kiến thức một cách hiệu quả.
Lý thuyết Điểm nằm giữa hai điểm. Tia Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu
1. Điểm nằm giữa 2 điểm
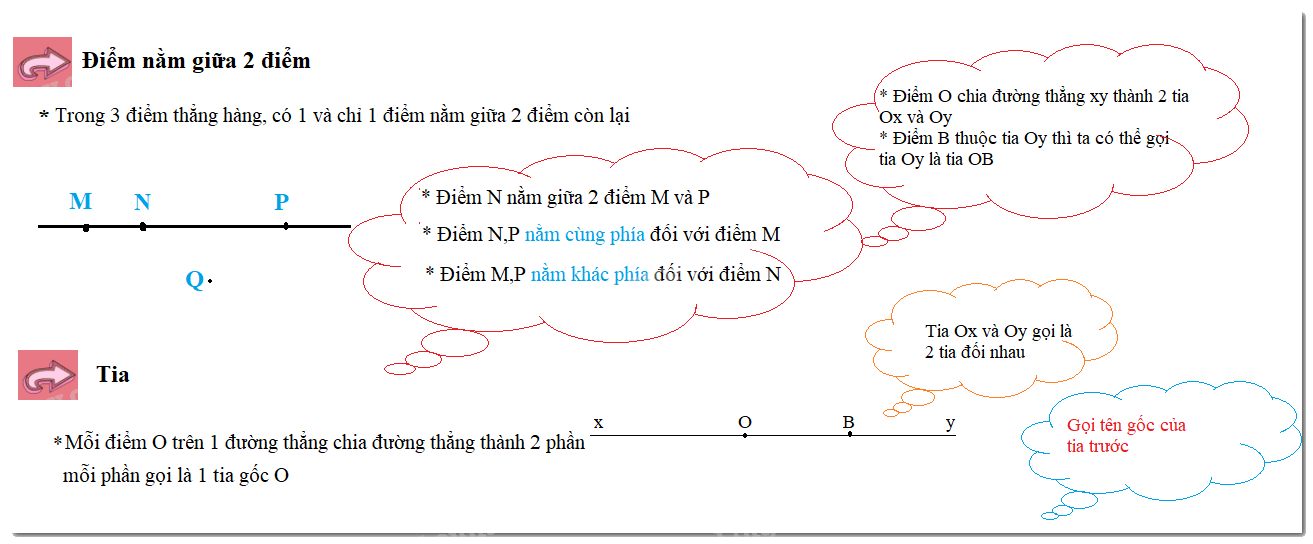
Trong ba điểm thẳng hàng, có một điểm và chỉ một điểm nằm giữa hai điểm còn lại.
3 điểm A,B,C cùng nằm trên đường thẳng d như hình sau
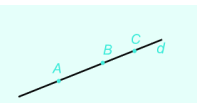
Điểm B nằm giữa 2 điểm A và C
2 điểm A và B nằm cùng phía đối với điểm C
2 điểm A và C nằm khác phía đối với điểm B
2. Tia
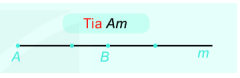
+Tia Am gồm điểm A, điểm B và các điểm nằm cùng phía với B đối với A. Tia Am còn được kí hiệu là tia AB. Điểm A là điểm gốc của tia
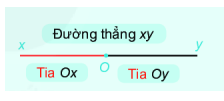
+Điểm O nằm trên đường thẳng xy chia đường thẳng thành 2 phần. Mỗi phần đó cùng với điểm O làm thành một tia. Khi đó 2 tia Ox và Oy gọi là 2 tia đối nhau
Nhận xét:

- Nếu hai tia \(OA\) và \(OB\) đối nhau thì điểm \(O\) nằm giữa hai điểm \(A\) và \(B\)
- Ngược lại, nếu điểm \(O\) nằm giữa hai điểm \(A\) và \(B\) thì:
+ Hai tia \(OA;OB\) đối nhau
+ Hai tia \(AO;AB\) trùng nhau; hai tia \(BO;BA\) trùng nhau
Trong hình học, việc hiểu rõ các khái niệm cơ bản như điểm, đường thẳng, đoạn thẳng và tia là vô cùng quan trọng. Bài viết này sẽ đi sâu vào Lý thuyết Điểm nằm giữa hai điểm. Tia Toán 6 KNTT, cung cấp kiến thức nền tảng và các ví dụ minh họa để giúp học sinh nắm vững kiến thức.
Xét ba điểm A, B, C nằm trên cùng một đường thẳng. Điểm B được gọi là nằm giữa hai điểm A và C nếu B không trùng với A và B không trùng với C. Điều này có nghĩa là B nằm trên đoạn thẳng AC.
Định nghĩa: Điểm B nằm giữa hai điểm A và C khi và chỉ khi AB + BC = AC.
Ví dụ: Cho ba điểm A, B, C thẳng hàng sao cho AB = 3cm, BC = 2cm. Khi đó, AC = AB + BC = 3cm + 2cm = 5cm. Vậy B nằm giữa A và C.
Định nghĩa: Tia gốc A là một phần của đường thẳng AB bao gồm điểm A và tất cả các điểm nằm trên đường thẳng AB về một phía của A.
Ký hiệu: Tia AB được ký hiệu là [AB].
Phân biệt tia và đoạn thẳng:
Ví dụ: Trên đường thẳng d, điểm A là gốc của tia AB và tia AC. Tuy nhiên, tia AB và tia AC là hai tia đối nhau.
Nếu điểm B nằm giữa hai điểm A và C, thì tia BA và tia BC là hai tia đối nhau. Ngược lại, nếu tia BA và tia BC là hai tia đối nhau, thì điểm B nằm giữa hai điểm A và C.
Bài 1: Cho ba điểm A, B, C thẳng hàng sao cho AB = 4cm, AC = 6cm. Tính độ dài đoạn thẳng BC.
Giải:
Có hai trường hợp xảy ra:
Vậy, BC có thể là 2cm hoặc 10cm.
Bài 2: Vẽ đường thẳng d. Lấy ba điểm A, B, C trên đường thẳng d sao cho B nằm giữa A và C. Vẽ tia BA và tia BC. Hai tia này có phải là hai tia đối nhau không? Vì sao?
Giải:
Vì B nằm giữa A và C nên tia BA và tia BC là hai tia đối nhau. Điều này là do tia BA và tia BC cùng gốc B và nằm trên cùng một đường thẳng d, nhưng lại hướng ngược nhau.
Lý thuyết về điểm nằm giữa và tia có ứng dụng thực tế trong nhiều lĩnh vực, chẳng hạn như:
Việc nắm vững Lý thuyết Điểm nằm giữa hai điểm. Tia Toán 6 KNTT không chỉ giúp học sinh giải quyết các bài toán trong sách giáo khoa mà còn rèn luyện tư duy logic và khả năng ứng dụng kiến thức vào thực tế.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về Lý thuyết Điểm nằm giữa hai điểm. Tia Toán 6 KNTT. Hãy luyện tập thường xuyên để nắm vững kiến thức và đạt kết quả tốt trong môn Toán.