Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 1 trang 10 sách bài tập Toán 12 Chân trời sáng tạo. Bài viết này cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 12, đáp ứng nhu cầu học tập của học sinh trên toàn quốc. Hãy cùng giaitoan.edu.vn khám phá lời giải bài 1 trang 10 ngay bây giờ!
Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 3.
Đề bài
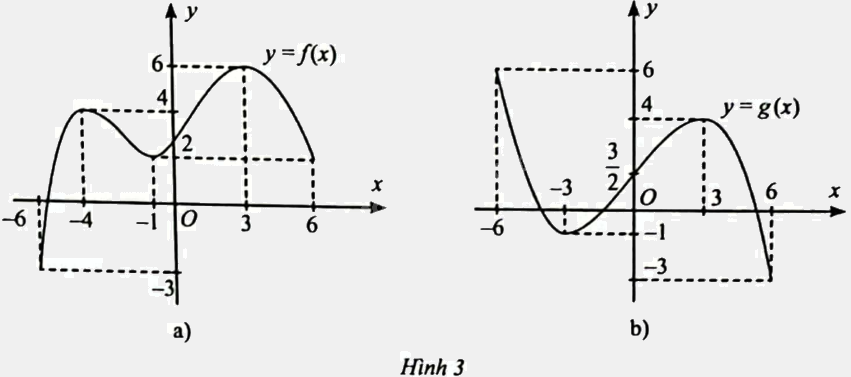
Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 3.
Phương pháp giải - Xem chi tiết
Dựa vào đồ thị hàm số.
Lời giải chi tiết
Hình 3a: Hàm số \(y = f\left( x \right)\) đồng biến trên các khoảng \(\left( { - 6; - 4} \right)\) và \(\left( { - 1;3} \right)\), nghịch biến trên các khoảng \(\left( { - 4; - 1} \right)\) và \(\left( {3;6} \right)\).
Hàm số \(y = f\left( x \right)\) có:
• \(x = - 1\) là điểm cực tiểu vì \(f\left( x \right) > f\left( { - 1} \right)\) với mọi \(x \in \left( { - 4;0} \right)\backslash \left\{ { - 1} \right\},{y_{CT}} = f\left( { - 1} \right) = 2\).
• \(x = 3\) là điểm cực đại vì \(f\left( x \right) < f\left( 3 \right)\) với mọi $x\in \left( 0;6 \right)\backslash \left\{ 3 \right\}, {{y}_{CĐ}}=f\left( 3 \right)=6$.
Hình 3b: Hàm số \(y = g\left( x \right)\) đồng biến trên khoảng \(\left( { - 3;3} \right)\), nghịch biến trên các khoảng \(\left( { - 6; - 3} \right)\) và \(\left( {3;6} \right)\).
Hàm số \(y = g\left( x \right)\) có:
• \(x = - 3\) là điểm cực tiểu vì \(g\left( x \right) > g\left( { - 3} \right)\) với mọi \(x \in \left( { - 6;0} \right)\backslash \left\{ { - 3} \right\},{y_{CT}} = g\left( { - 3} \right) = - 1\).
• \(x = 3\) là điểm cực đại vì \(g\left( x \right) < g\left( 3 \right)\) với mọi $x\in \left( 0;6 \right)\backslash \left\{ 3 \right\},{{y}_{CĐ}}=g\left( 3 \right)=4$.
Bài 1 trang 10 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học về giới hạn của hàm số. Đây là một phần kiến thức nền tảng quan trọng trong chương trình Toán 12, giúp học sinh hiểu rõ hơn về khái niệm giới hạn và ứng dụng của nó trong việc giải các bài toán liên quan đến hàm số.
Bài 1 yêu cầu học sinh tính giới hạn của các hàm số khi x tiến tới một giá trị cụ thể. Các hàm số thường gặp trong bài tập này bao gồm các hàm đa thức, hàm phân thức, và các hàm số đặc biệt khác. Để giải bài tập này, học sinh cần nắm vững các quy tắc tính giới hạn, bao gồm:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi xin trình bày lời giải chi tiết cho từng câu hỏi trong bài 1 trang 10 sách bài tập Toán 12 Chân trời sáng tạo.
Để tính giới hạn này, chúng ta có thể thay trực tiếp x = 2 vào hàm số 2x + 1. Khi đó, ta có:
lim (2x + 1) = 2 * 2 + 1 = 5
Vậy, lim (2x + 1) khi x → 2 bằng 5.
Khi thay trực tiếp x = 2 vào hàm số (x^2 - 4) / (x - 2), ta được 0/0, là một dạng vô định. Do đó, chúng ta cần phân tích tử số và mẫu số để rút gọn biểu thức trước khi tính giới hạn.
(x^2 - 4) / (x - 2) = (x - 2)(x + 2) / (x - 2) = x + 2 (với x ≠ 2)
Vậy, lim (x^2 - 4) / (x - 2) = lim (x + 2) = 2 + 2 = 4
Vậy, lim (x^2 - 4) / (x - 2) khi x → 2 bằng 4.
Đây là một giới hạn đặc biệt, và chúng ta biết rằng lim (sin x) / x = 1 khi x → 0.
Khi giải bài tập về giới hạn, học sinh cần lưu ý một số điều sau:
Kiến thức về giới hạn có nhiều ứng dụng trong toán học và các lĩnh vực khác, bao gồm:
Bài 1 trang 10 sách bài tập Toán 12 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về giới hạn của hàm số. Hy vọng rằng với lời giải chi tiết và các lưu ý trên, học sinh có thể tự tin giải bài tập này và nắm vững kiến thức về giới hạn.
Giaitoan.edu.vn luôn đồng hành cùng học sinh trên con đường chinh phục tri thức. Hãy truy cập website của chúng tôi để tìm hiểu thêm về các bài giải Toán 12 và các tài liệu học tập hữu ích khác.