Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 7 trang 60 sách bài tập Toán 12 chương trình Chân trời sáng tạo. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong các kỳ thi.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải bài 7 trang 60 một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Một khu vực đã được thiết lập một hệ toạ độ \(Oxyz\) (đơn vị trên các trục là mét). Một flycam đang phát sóng wifi bao phủ một vùng không gian bên trong mặt cầu \(\left( S \right):{\left( {x - 20} \right)^2} + {\left( {y - 30} \right)^2} + {\left( {z - 10} \right)^2} = 400\). Một người đang sử dụng máy tính tại điểm \(M\) nằm trên điểm giao của mặt cầu \(\left( S \right)\) và mặt đất \(\left( P \right):z = 0\). a) Xác định toạ độ tâm \(I\) và bán kính của mặt cầu \(\left( S \right)\). Tính kho
Đề bài
Một khu vực đã được thiết lập một hệ toạ độ \(Oxyz\) (đơn vị trên các trục là mét). Một flycam đang phát sóng wifi bao phủ một vùng không gian bên trong mặt cầu \(\left( S \right):{\left( {x - 20} \right)^2} + {\left( {y - 30} \right)^2} + {\left( {z - 10} \right)^2} = 400\). Một người đang sử dụng máy tính tại điểm \(M\) nằm trên điểm giao của mặt cầu \(\left( S \right)\) và mặt đất \(\left( P \right):z = 0\).
a) Xác định toạ độ tâm \(I\) và bán kính của mặt cầu \(\left( S \right)\). Tính khoảng cách \(IJ\) của đoạn vuông góc từ \(I\) đến \(\left( P \right)\).
b) Tính độ dài đoạn thẳng \(JM\). Làm tròn kết quả đến hàng phần trăm của mét.
Phương pháp giải - Xem chi tiết
‒ Mặt cầu \(\left( S \right):{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\) có tâm \(I\left( {a;b;c} \right)\) bán kính \(R\).
‒ Khoảng cách \(IJ\) của đoạn vuông góc từ \(I\) đến \(\left( P \right)\) chính là khoảng cách từ \(I\) đến \(\left( P \right)\).
‒ Khoảng cách từ điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng \(\left( P \right):Ax + By + C{\rm{z}} + D = 0\):
\(d\left( {{M_0};\left( P \right)} \right) = \frac{{\left| {A{x_0} + B{y_0} + C{{\rm{z}}_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).
Lời giải chi tiết
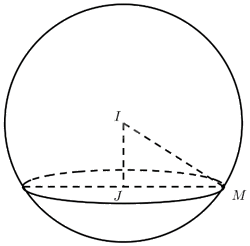
a) Mặt cầu \(\left( S \right):{\left( {x - 20} \right)^2} + {\left( {y - 30} \right)^2} + {\left( {z - 10} \right)^2} = 400\) có tâm \(I\left( {20;30;10} \right)\) bán kính \(R = \sqrt {400} = 20\).
\(IJ = d\left( {I;\left( P \right)} \right) = \frac{{\left| {10} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} }} = 10\left( m \right)\).
b) Ta có \(M \in \left( S \right)\) nên \(IM = R = 20\).
Tam giác \(IJM\) vuông tại \(J\) nên ta có:
\(JM = \sqrt {I{M^2} - I{J^2}} = \sqrt {{{20}^2} - {{10}^2}} = 10\sqrt 3 \approx 17,32\left( m \right)\).
Bài 7 trang 60 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học về đạo hàm. Bài tập này thường tập trung vào việc vận dụng các quy tắc tính đạo hàm của các hàm số cơ bản như hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit và các phép toán trên hàm số. Mục tiêu chính là giúp học sinh rèn luyện kỹ năng tính đạo hàm và ứng dụng đạo hàm để giải quyết các bài toán thực tế.
Bài 7 thường bao gồm các dạng bài tập sau:
Để giải bài 7 trang 60 sách bài tập Toán 12 Chân trời sáng tạo một cách hiệu quả, bạn cần:
Ví dụ 1: Tính đạo hàm của hàm số f(x) = 3x2 + 2x - 1.
Giải:
f'(x) = 6x + 2
Ví dụ 2: Tìm đạo hàm cấp hai của hàm số g(x) = sin(x).
Giải:
g'(x) = cos(x)
g''(x) = -sin(x)
Để giải nhanh các bài tập về đạo hàm, bạn có thể sử dụng các mẹo sau:
Để học tập và ôn luyện kiến thức về đạo hàm, bạn có thể tham khảo các tài liệu sau:
Bài 7 trang 60 sách bài tập Toán 12 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Bằng cách nắm vững các quy tắc tính đạo hàm, hiểu rõ các khái niệm liên quan và luyện tập thường xuyên, bạn có thể tự tin giải quyết các bài tập về đạo hàm một cách hiệu quả. Chúc bạn học tập tốt!