Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 4 trang 86 sách bài tập Toán 12 Chân trời sáng tạo. Bài viết này cung cấp phương pháp giải bài tập một cách rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác và cập nhật nhất để hỗ trợ tối đa cho quá trình học tập của bạn. Hãy cùng theo dõi và tham khảo!
Chọn đúng hoặc sai cho mỗi ý a, b, c, d. Cho sơ đồ hình cây dưới đây: a) Xác suất của biến cố (B) với điều kiện (A) không xảy ra là 0,6. b) Xác suất cả hai biến cố (A) và (B) đều xảy ra là 0,3. c) Xác suất của biến cố (B) là 0,9. d) Xác suất của biến cố (A) với điều kiện (B) là (frac{1}{{19}}).
Đề bài
Chọn đúng hoặc sai cho mỗi ý a, b, c, d.
Cho sơ đồ hình cây dưới đây:
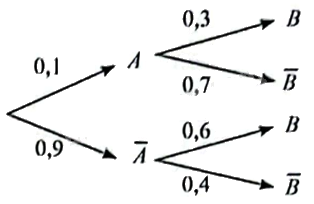
a) Xác suất của biến cố \(B\) với điều kiện \(A\) không xảy ra là 0,6.
b) Xác suất cả hai biến cố \(A\) và \(B\) đều xảy ra là 0,3.
c) Xác suất của biến cố \(B\) là 0,9.
d) Xác suất của biến cố \(A\) với điều kiện \(B\) là \(\frac{1}{{19}}\).
Phương pháp giải - Xem chi tiết
‒ Dựa vào sơ đồ hình cây.
‒ Sử dụng công thức tính xác suất toàn phần: \(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
‒ Sử dụng công thức Bayes: \(P\left( {B|A} \right) = \frac{{P\left( B \right).P\left( {A|B} \right)}}{{P\left( A \right)}}\).
Lời giải chi tiết
Theo sơ đồ hình cây ta có xác suất của biến cố \(B\) với điều kiện \(A\) không xảy ra là \(P\left( {B|\overline A } \right) = 0,6\). Vậy a) đúng.
Theo sơ đồ hình cây ta có xác suất của cả hai biến cố \(A\) và \(B\) đều xảy ra là \(P\left( {B|A} \right) = 0,3\). Vậy b) đúng.
Theo sơ đồ hình cây ta có: \(P\left( A \right) = 0,1;P\left( {\overline A } \right) = 0,9\).
Theo công thức xác suất toàn phần ta có:
\(P\left( B \right) = P\left( A \right).P\left( {B|A} \right) + P\left( {\overline A } \right).P\left( {B|\overline A } \right) = 0,1.0,3 + 0,9.0,6 = 0,57\).
Vậy c) sai.
Theo công thức Bayes, ta có: \(P\left( {A|B} \right) = \frac{{P\left( A \right).P\left( {B|A} \right)}}{{P\left( B \right)}} = \frac{{0,9.0,3}}{{0,57}} = \frac{1}{{19}}\). Vậy d) đúng.
a) Đ.
b) Đ.
c) S.
d) Đ.
Bài 4 trang 86 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, đạo hàm của tổng, hiệu, tích, thương của các hàm số, và quy tắc đạo hàm của hàm hợp để giải quyết các bài toán cụ thể. Việc nắm vững các khái niệm và công thức đạo hàm là yếu tố then chốt để hoàn thành tốt bài tập này.
Bài 4 thường bao gồm các dạng bài tập sau:
Để giải quyết bài 4 trang 86 sách bài tập Toán 12 Chân trời sáng tạo một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:
Ví dụ: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Giải:
f'(x) = (x3)' + (2x2)' - (5x)' + (1)'
f'(x) = 3x2 + 4x - 5 + 0
f'(x) = 3x2 + 4x - 5
Dưới đây là một số lưu ý quan trọng khi giải bài 4 trang 86 sách bài tập Toán 12 Chân trời sáng tạo:
Để hỗ trợ quá trình học tập và giải bài tập, bạn có thể tham khảo các tài liệu sau:
Bài 4 trang 86 sách bài tập Toán 12 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Bằng cách nắm vững các công thức đạo hàm, thực hiện các phép biến đổi đại số một cách cẩn thận và luyện tập thường xuyên, bạn có thể giải quyết bài tập này một cách hiệu quả. Chúc bạn học tập tốt!