Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12 sách Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn giải bài 2 trang 20 một cách đầy đủ và chính xác.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Tính diện tích của hình phẳng được gạch chéo trong mỗi hình sau.
Đề bài
Tính diện tích của hình phẳng được gạch chéo trong mỗi hình sau.
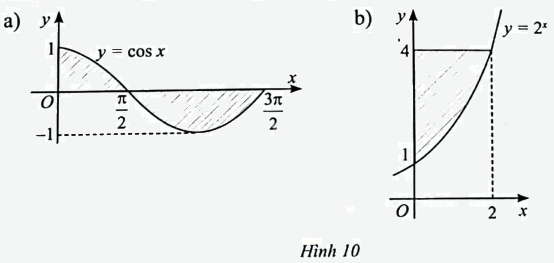
Phương pháp giải - Xem chi tiết
‒ Sử dụng công thức: Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b\) là: \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \).
‒ Sử dụng công thức: Tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số \(y = f\left( x \right),y = g\left( x \right)\) và hai đường thẳng \(x = a,x = b\) là: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Lời giải chi tiết
a) \(S = \int\limits_0^{\frac{{3\pi }}{2}} {\left| {\cos x} \right|dx} = \int\limits_0^{\frac{\pi }{2}} {\cos xdx} + \int\limits_{\frac{\pi }{2}}^{\frac{{3\pi }}{2}} {\left( { - \cos x} \right)dx} = \left. {\sin x} \right|_0^{\frac{\pi }{2}} - \left. {\sin x} \right|_{\frac{\pi }{2}}^{\frac{{3\pi }}{2}} = 3\).
b) \(S = \int\limits_0^2 {\left| {4 - {2^x}} \right|dx} = \int\limits_0^2 {\left( {4 - {2^x}} \right)dx} = \left. {\left( {4{\rm{x}} - \frac{{{2^x}}}{{\ln }}} \right)} \right|_0^2 = 8 - \frac{3}{{\ln 2}}\).
Bài 2 trang 20 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, quy tắc tính đạo hàm, và các ứng dụng của đạo hàm để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức nền tảng và luyện tập thường xuyên là chìa khóa để giải quyết thành công bài tập này.
Bài 2 thường bao gồm các dạng bài tập sau:
Để giải bài 2 trang 20 một cách hiệu quả, bạn cần thực hiện các bước sau:
Ví dụ: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Giải:
f'(x) = 3x2 + 4x - 5
Để học tập và ôn luyện kiến thức về đạo hàm, bạn có thể tham khảo các tài liệu sau:
Bài 2 trang 20 sách bài tập Toán 12 Chân trời sáng tạo là một bài tập quan trọng giúp bạn củng cố kiến thức về đạo hàm. Hy vọng rằng với hướng dẫn chi tiết và các mẹo giải bài tập hiệu quả mà chúng tôi đã cung cấp, bạn sẽ giải quyết thành công bài tập này và đạt kết quả tốt trong môn Toán.