Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 2 trang 63 sách bài tập Toán 12 Chân trời sáng tạo. Bài viết này cung cấp phương pháp giải bài tập một cách rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 12 Chân trời sáng tạo, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
Cho tứ diện \(OABC\). Tìm các vectơ: a) \(\overrightarrow {OA} + \overrightarrow {AB} - \overrightarrow {OC} \); b) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} \).
Đề bài
Cho tứ diện \(OABC\). Tìm các vectơ:
a) \(\overrightarrow {OA} + \overrightarrow {AB} - \overrightarrow {OC} \);
b) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} \).
Phương pháp giải - Xem chi tiết
Sử dụng quy tắc ba điểm, quy tắc trừ, quy tắc hình hộp.
Lời giải chi tiết
a) \(\overrightarrow {OA} + \overrightarrow {AB} - \overrightarrow {OC} = \overrightarrow {OB} - \overrightarrow {OC} = \overrightarrow {CB} \).
b) Vẽ hình hộp \(OADB.CFEK\).
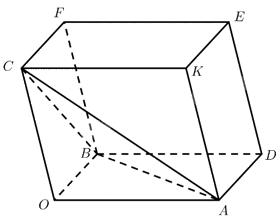
Theo quy tắc hình hộp ta có:
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OE} \).
Bài 2 trang 63 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, quy tắc tính đạo hàm, và các ứng dụng của đạo hàm để giải quyết các bài toán cụ thể.
Thông thường, bài 2 trang 63 sẽ bao gồm các dạng bài tập sau:
Để giải bài 2 trang 63 sách bài tập Toán 12 Chân trời sáng tạo một cách hiệu quả, bạn cần:
Giả sử bài 2 trang 63 yêu cầu tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1. Ta có:
f'(x) = 3x2 + 4x - 5
Dạng 1: Tính đạo hàm của hàm số tại một điểm
Để tính đạo hàm của hàm số f(x) tại một điểm x0, ta thực hiện các bước sau:
Dạng 2: Tìm đạo hàm của hàm số
Để tìm đạo hàm của hàm số f(x), ta thực hiện các bước sau:
Khi giải bài tập về đạo hàm, bạn cần lưu ý:
Để học tập và ôn luyện kiến thức về đạo hàm, bạn có thể tham khảo các tài liệu sau:
Bài 2 trang 63 sách bài tập Toán 12 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin giải quyết bài tập một cách hiệu quả.