Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 6 trang 71 sách bài tập Toán 12 Chân trời sáng tạo. Bài viết này cung cấp đáp án, phương pháp giải và giải thích rõ ràng, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, dễ hiểu và cập nhật mới nhất để hỗ trợ tối đa cho quá trình học tập của bạn.
Cho hình hộp \(ABCD.A'B'C'D'\) có \(A\left( {2;0;2} \right),B\left( {4;2;4} \right),D\left( {2; - 2;2} \right),C'\left( {8;10; - 10} \right)\). Tìm toạ độ điểm \(A'\).
Đề bài
Cho hình hộp \(ABCD.A'B'C'D'\) có \(A\left( {2;0;2} \right),B\left( {4;2;4} \right),D\left( {2; - 2;2} \right),C'\left( {8;10; - 10} \right)\). Tìm toạ độ điểm \(A'\).
Phương pháp giải - Xem chi tiết
‒ Sử dụng toạ độ của vectơ \(\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A}} \right)\).
‒ Sử dụng tính chất hai vectơ bằng nhau: Với \(\overrightarrow u = \left( {{x_1};{y_1};{z_1}} \right)\) và \(\overrightarrow v = \left( {{x_2};{y_2};{z_2}} \right)\), ta có: \(\overrightarrow u = \overrightarrow v \Leftrightarrow \left\{ \begin{array}{l}{x_1} = {x_2}\\{y_1} = {y_2}\\{z_1} = {z_2}\end{array} \right.\).
Lời giải chi tiết
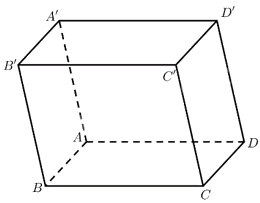
Giả sử \(D\left( {{x_C};{y_C};{z_C}} \right)\). Ta có
\(\overrightarrow {AD} = \left( {2 - 2; - 2 - 0;2 - 2} \right) = \left( {0; - 2;0} \right)\).
\(\overrightarrow {BC} = \left( {{x_C} - 4;{y_C} - 2;{z_C} - 4} \right)\).
\(ABCD\) là hình bình hành nên \(\overrightarrow {AD} = \overrightarrow {BC} \).
\( \Leftrightarrow \left\{ \begin{array}{l}{x_C} - 4 = 0\\{y_C} - 2 = - 2\\{z_C} - 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 4\\{y_C} = 0\\{z_C} = 4\end{array} \right.\). Vậy \(C\left( {4;0;4} \right)\).
Giả sử \(A'\left( {{x_{A'}};{y_{A'}};{z_{A'}}} \right)\). Ta có
\(\overrightarrow {AA'} = \left( {{x_{A'}} - 2;{y_{A'}};{z_{A'}} - 2} \right)\).
\(\overrightarrow {CC'} = \left( {8 - 4;10 - 0; - 10 - 4} \right) = \left( {4;10; - 14} \right)\).
\(ABCD\) là hình bình hành nên \(\overrightarrow {AD} = \overrightarrow {BC} \).
\( \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} - 2 = 4\\{y_{A'}} = 10\\{z_{A'}} - 2 = - 14\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} = 6\\{y_{A'}} = 10\\{z_{A'}} = - 12\end{array} \right.\). Vậy \(A'\left( {6;10; - 12} \right)\).
Bài 6 trang 71 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học về đạo hàm. Bài tập này thường tập trung vào việc vận dụng các quy tắc tính đạo hàm của hàm số, đặc biệt là đạo hàm của tổng, hiệu, tích, thương và đạo hàm hàm hợp. Việc nắm vững các quy tắc này là nền tảng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Bài 6 thường bao gồm các dạng bài tập sau:
Để giải quyết bài 6 trang 71 sách bài tập Toán 12 Chân trời sáng tạo một cách hiệu quả, bạn cần:
Ví dụ: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Giải:
f'(x) = (x3)' + (2x2)' - (5x)' + (1)'
f'(x) = 3x2 + 4x - 5 + 0
f'(x) = 3x2 + 4x - 5
Một số lưu ý quan trọng khi giải bài tập về đạo hàm:
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, bạn có thể luyện tập thêm với các bài tập sau:
Bài 6 trang 71 sách bài tập Toán 12 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính đạo hàm và ứng dụng đạo hàm để giải quyết các bài toán thực tế. Hy vọng với những hướng dẫn và ví dụ minh họa trên, bạn sẽ tự tin hơn khi giải quyết bài tập này và các bài tập tương tự trong chương trình học.