Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 8 trang 64 sách bài tập Toán 12 Chân trời sáng tạo. Bài viết này cung cấp đáp án, phương pháp giải và giải thích rõ ràng từng bước để giúp học sinh hiểu bài và làm bài tập một cách hiệu quả.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, dễ hiểu và cập nhật mới nhất để hỗ trợ tối đa cho quá trình học tập của bạn.
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\). Gọi \(x,y,z\) theo thứ tự là số đo các góc hợp bởi vectơ \(\overrightarrow {AC'} \) với các vectơ \(\overrightarrow {AB} ,\overrightarrow {AD} ,\overrightarrow {AA'} \). Chứng minh \({\cos ^2}x + {\cos ^2}y + {\cos ^2}z = 1\).
Đề bài
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\). Gọi \(x,y,z\) theo thứ tự là số đo các góc hợp bởi vectơ \(\overrightarrow {AC'} \) với các vectơ \(\overrightarrow {AB} ,\overrightarrow {AD} ,\overrightarrow {AA'} \).
Chứng minh \({\cos ^2}x + {\cos ^2}y + {\cos ^2}z = 1\).
Phương pháp giải - Xem chi tiết
Sử dụng định lý Pitago.
Lời giải chi tiết
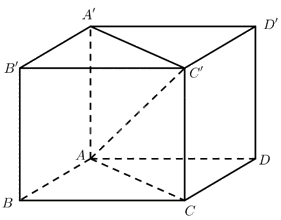
Gọi \(a,b,c,d\) lần lượt là độ dài của \(AB,A{\rm{D}},AA',AC'\).
Tam giác \(ABC\) vuông tại \(B \Rightarrow A{C^2} = A{B^2} + B{C^2}\).
Tam giác \(ACC'\) vuông tại \(C\)
\( \Rightarrow AC{'^2} = A{C^2} + CC{'^2} = A{B^2} + B{C^2} + AA{'^2}\)
Do đó \({d^2} = {a^2} + {b^2} + {c^2}\).
Ta có: \(\cos x = \frac{{AB}}{{AC'}} = \frac{a}{d},\cos y = \frac{{AD}}{{AC'}} = \frac{b}{d},\cos z = \frac{{AA'}}{{AC'}} = \frac{c}{d}\)
\({\cos ^2}x + {\cos ^2}y + {\cos ^2}z = {\left( {\frac{a}{d}} \right)^2} + {\left( {\frac{b}{d}} \right)^2} + {\left( {\frac{c}{d}} \right)^2} = \frac{{{a^2}}}{{{d^2}}} + \frac{{{b^2}}}{{{d^2}}} + \frac{{{c^2}}}{{{d^2}}} = \frac{{{a^2} + {b^2} + {c^2}}}{{{d^2}}} = \frac{{{d^2}}}{{{d^2}}} = 1\).
Bài 8 trang 64 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học về đạo hàm. Bài tập này thường tập trung vào việc vận dụng các quy tắc tính đạo hàm của các hàm số cơ bản, hàm hợp và các hàm lượng giác. Việc nắm vững kiến thức về đạo hàm là vô cùng quan trọng, không chỉ cho kỳ thi THPT Quốc gia mà còn là nền tảng cho các môn học nâng cao ở bậc đại học.
Bài 8 thường bao gồm các dạng bài tập sau:
Để giải quyết hiệu quả các bài tập trong bài 8, học sinh cần:
Ví dụ: Tính đạo hàm của hàm số f(x) = 3x2 + 2sin(x) - 5.
Giải:
f'(x) = d/dx (3x2) + d/dx (2sin(x)) - d/dx (5)
f'(x) = 6x + 2cos(x) - 0
f'(x) = 6x + 2cos(x)
Một số lưu ý quan trọng khi giải bài tập về đạo hàm:
Để học tốt môn Toán 12 và giải quyết các bài tập về đạo hàm, bạn có thể tham khảo các tài liệu sau:
Bài 8 trang 64 sách bài tập Toán 12 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Bằng cách nắm vững các công thức, quy tắc và luyện tập thường xuyên, bạn có thể giải quyết hiệu quả các bài tập này và đạt kết quả tốt trong môn Toán.