Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12 Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 6 trang 11 sách bài tập, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Đạo hàm (f'left( x right)) của hàm số (y = fleft( x right)) có đồ thị như Hình 4. Xét tính đơn điệu và tìm các điểm cực trị của hàm số (y = fleft( x right)).
Đề bài
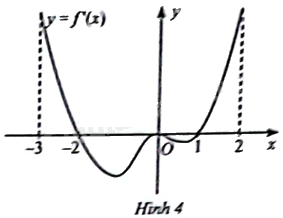
Đạo hàm \(f'\left( x \right)\) của hàm số \(y = f\left( x \right)\) có đồ thị như Hình 4. Xét tính đơn điệu và tìm các điểm cực trị của hàm số \(y = f\left( x \right)\).
Phương pháp giải - Xem chi tiết
Từ đồ thị hàm số \(y = f'\left( x \right)\), lập bảng biến thiên của hàm số \(y = f\left( x \right)\) rồi xác định tính đồng biến, nghịch biến, cực trị của hàm số.
Lời giải chi tiết
Từ đồ thị, ta có \(f'\left( x \right) > 0\) trên các khoảng \(\left( { - 3; - 2} \right)\) và \(\left( {1;2} \right)\), \(f'\left( x \right) < 0\) trên các khoảng \(\left( { - 2;0} \right)\) và \(\left( {0;1} \right)\). Do đó ta có bảng biến thiên:
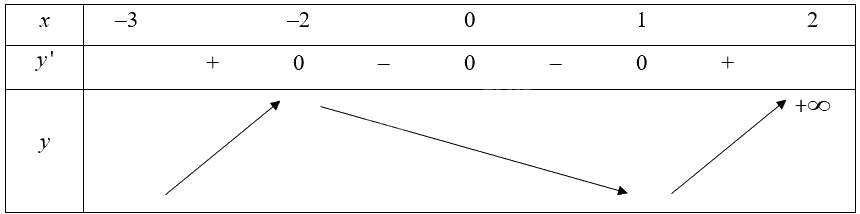
Hàm số \(y = f\left( x \right)\) đồng biến trên các khoảng \(\left( { - 3; - 2} \right)\) và \(\left( {1;2} \right)\), nghịch biến trên khoảng \(\left( { - 2;1} \right)\).
Hàm số đạt cực đại tại \(x = - 2\) và đạt cực tiểu tại \({\rm{x}} = 1\).
Bài 6 trang 11 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, quy tắc tính đạo hàm, và các ứng dụng của đạo hàm để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức nền tảng và luyện tập thường xuyên là chìa khóa để thành công trong việc giải bài tập này.
Bài 6 thường bao gồm các dạng bài tập sau:
Để giải bài 6 trang 11 một cách hiệu quả, bạn cần thực hiện theo các bước sau:
Ví dụ: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Giải:
f'(x) = 3x2 + 4x - 5
Để giải nhanh các bài tập về đạo hàm, bạn có thể sử dụng các mẹo sau:
Khi giải các bài tập về đạo hàm, bạn cần lưu ý những điều sau:
Để học tập và ôn luyện kiến thức về đạo hàm, bạn có thể tham khảo các tài liệu sau:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải bài 6 trang 11 sách bài tập Toán 12 Chân trời sáng tạo một cách hiệu quả. Chúc bạn học tập tốt!