Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài 2 trang 109 sách bài tập Toán 12 - Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt kết quả cao trong môn Toán.
Người ta đo độ ẩm không khí lúc 12 giờ trưa mỗi ngày tại một địa điểm trong tháng 4. Kết quả các lần đo được biểu diễn ở biểu đồ tần số tương đối ghép nhóm dưới đây. a) Hãy lập bảng tần số ghép nhóm cho dữ liệu ở biểu đồ trên. b) Hãy tính các số đặc trưng đo mức độ phân tán của mẫu số liệu ghép nhóm trên. (Làm tròn kết quả đến hàng phần nghìn.)
Đề bài
Người ta đo độ ẩm không khí lúc 12 giờ trưa mỗi ngày tại một địa điểm trong tháng 4. Kết quả các lần đo được biểu diễn ở biểu đồ tần số tương đối ghép nhóm dưới đây.
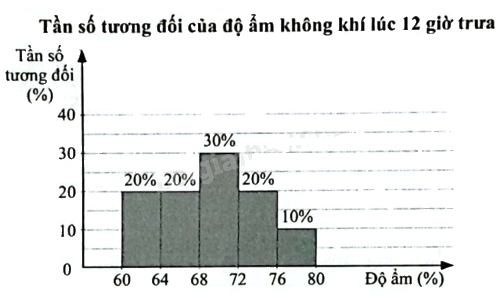
a) Hãy lập bảng tần số ghép nhóm cho dữ liệu ở biểu đồ trên.
b) Hãy tính các số đặc trưng đo mức độ phân tán của mẫu số liệu ghép nhóm trên. (Làm tròn kết quả đến hàng phần nghìn.)
Phương pháp giải - Xem chi tiết
‒ Sử dụng công thức tính khoảng biến thiên của mẫu số liệu ghép nhóm: \(R = {a_{m + 1}} - {a_1}\).
‒ Sử dụng công thức tính các tứ phân vị của mẫu số liệu ghép nhóm:
Tứ phân vị thứ \(k\) được xác định như sau: \({Q_k} = {u_m} + \frac{{\frac{{kn}}{4} - C}}{{{n_m}}}\left( {{u_{m + 1}} - {u_m}} \right)\)
trong đó:
• \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu;
• \(\left[ {{u_m};{u_{m + 1}}} \right)\) là nhóm chứa tứ phân vị thứ \(k\);
• \({n_m}\) là tần số của nhóm chứa tứ phân vị thứ \(k\);
• \(C = {n_1} + {n_2} + ... + {n_{m - 1}}\).
‒ Sử dụng công thức tính khoảng tứ phân vị của mẫu số liệu ghép nhóm: \(\Delta Q = {Q_3} - {Q_1}\).
‒ Sử dụng công thức tính phương sai của mẫu số liệu ghép nhóm:
\(\begin{array}{l}{S^2} = \frac{1}{n}\left[ {{n_1}{{\left( {{c_1} - \overline x } \right)}^2} + {n_2}{{\left( {{c_2} - \overline x } \right)}^2} + ... + {n_k}{{\left( {{c_k} - \overline x } \right)}^2}} \right]\\ & = \frac{1}{n}\left[ {{n_1}c_1^2 + {n_2}c_2^2 + ... + {n_k}c_k^2} \right] - {\overline x ^2}\end{array}\)
‒ Sử dụng công thức tính độ lệch chuẩn của mẫu số liệu ghép nhóm: \(S = \sqrt {{S^2}} \).
Lời giải chi tiết
a) Ta có bảng tần số ghép nhóm:

b) Khoảng biến thiên của mẫu số liệu trên là: \(R = 80 - 60 = 30\) (%).
Gọi \({x_1};{x_2};...;{x_{30}}\) là mẫu số liệu gốc theo thứ tự không giảm.
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({x_8} \in \left[ {64;68} \right)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
\({Q_1} = 64 + \frac{{\frac{{1.30}}{4} - 6}}{6}\left( {68 - 64} \right) = 65\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{23}} \in \left[ {72;76} \right)\). Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
\({Q_3} = 72 + \frac{{\frac{{3.30}}{4} - \left( {6 + 6 + 9} \right)}}{6}\left( {68 - 64} \right) = 73\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
\(\Delta Q = {Q_3} - {Q_1} = 73 - 65 = 8\) (%).
Ta có bảng sau:

Cỡ mẫu \(n = 30\)
Số trung bình của mẫu số liệu ghép nhóm là:
\(\overline x = \frac{{6.62 + 6.66 + 9.70 + 6.74 + 3.78}}{{30}} = 69,2\)
Phương sai của mẫu số liệu ghép nhóm đó là:
\({S^2} = \frac{1}{{30}}\left( {{{6.62}^2} + {{6.66}^2} + {{9.70}^2} + {{6.74}^2} + {{3.78}^2}} \right) - {69,2^2} = 24,96\)
Độ lệch chuẩn của mẫu số liệu ghép nhóm là: \(S = \sqrt {24,96} \approx 4,996\).
Bài 2 trang 109 sách bài tập Toán 12 - Chân trời sáng tạo thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, đạo hàm của tổng, hiệu, tích, thương của các hàm số, và đạo hàm của hàm hợp để giải quyết các bài toán cụ thể. Việc nắm vững các quy tắc đạo hàm và kỹ năng biến đổi đại số là rất quan trọng để hoàn thành bài tập này một cách chính xác.
Trước khi bắt đầu giải bài tập, điều quan trọng là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 2 trang 109, học sinh cần xác định hàm số cần tìm đạo hàm, các quy tắc đạo hàm nào cần áp dụng, và cách trình bày lời giải một cách rõ ràng và logic.
Để giúp bạn hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ cung cấp lời giải chi tiết từng bước. Lưu ý rằng, có thể có nhiều cách giải khác nhau cho cùng một bài toán, nhưng chúng tôi sẽ trình bày một cách giải phổ biến và dễ hiểu nhất.
Vậy, đạo hàm của hàm số f(x) = x^2 + 3x - 2 là f'(x) = 2x + 3.
Trong chương trình học về đạo hàm, học sinh thường gặp các dạng bài tập sau:
Để giải quyết các dạng bài tập này, học sinh cần nắm vững các quy tắc đạo hàm, kỹ năng biến đổi đại số, và khả năng phân tích bài toán để lựa chọn phương pháp giải phù hợp.
Để học tập môn Toán hiệu quả, đặc biệt là phần đạo hàm, bạn có thể áp dụng các mẹo sau:
Bài 2 trang 109 sách bài tập Toán 12 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Hy vọng rằng, với lời giải chi tiết và các hướng dẫn trong bài viết này, bạn sẽ tự tin hơn khi giải quyết các bài tập tương tự. Chúc bạn học tập tốt!