Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 12 trang 12 sách bài tập Toán 12 Chân trời sáng tạo. Bài viết này cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng, dễ hiểu, phù hợp với chương trình học Toán 12 hiện hành. Hãy cùng giaitoan.edu.vn khám phá lời giải bài tập này ngay nhé!
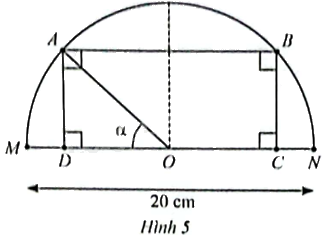
Cho điểm \(A\) di động trên nửa đường tròn tâm \(O\) đường kính \(MN = 20{\rm{ }}cm,\widehat {MOA} = \alpha \) với \(0 \le \alpha \le \pi \). Lấy điểm \(B\) thuộc nửa đường tròn và \(C,D\) thuộc đường kính \(MN\) được xác định sao cho \(ABCD\) là hình chữ nhật. Khi \(A\) di động từ trái sang phải, trong các khoảng nào của \(\alpha \) thì diện tích của hình chữ nhật \(ABCD\) tăng, trong các khoảng nào của \(\alpha \) thì diện tích của hình chữ nhật \(ABCD\) giảm?
Đề bài
Cho điểm \(A\) di động trên nửa đường tròn tâm \(O\) đường kính \(MN = 20{\rm{ }}cm,\widehat {MOA} = \alpha \) với \(0 \le \alpha \le \pi \). Lấy điểm \(B\) thuộc nửa đường tròn và \(C,D\) thuộc đường kính \(MN\) được xác định sao cho \(ABCD\) là hình chữ nhật. Khi \(A\) di động từ trái sang phải, trong các khoảng nào của \(\alpha \) thì diện tích của hình chữ nhật \(ABCD\) tăng, trong các khoảng nào của \(\alpha \) thì diện tích của hình chữ nhật \(ABCD\) giảm?
Phương pháp giải - Xem chi tiết
Lập hàm số \(y = f\left( \alpha \right)\) trên đoạn \(\left[ {0;\pi } \right]\), lập bảng biến thiên và tìm khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết
Ta có: \(A{\rm{D}} = OA\sin \alpha = 10\sin \alpha ;O{\rm{D}} = OA\cos \alpha = 10\cos \alpha ;C{\rm{D}} = 2{\rm{OD}} = 20\cos \alpha \).
Diện tích hình chữ nhật là: \(AD.C{\rm{D}} = 10\sin \alpha .20\cos \alpha = 200\sin \alpha \cos \alpha = 100\sin 2\alpha \).
Xét hàm số \(f\left( \alpha \right) = 100\sin 2\alpha \) trên đoạn \(\left[ {0;\pi } \right]\).
Ta có:
\(f'\left( \alpha \right) = 200\cos 2\alpha ;f'\left( \alpha \right) = 0 \Leftrightarrow \alpha = \frac{\pi }{4}\) hoặc \(\alpha = \frac{{3\pi }}{4}\).
Bảng biến thiên:
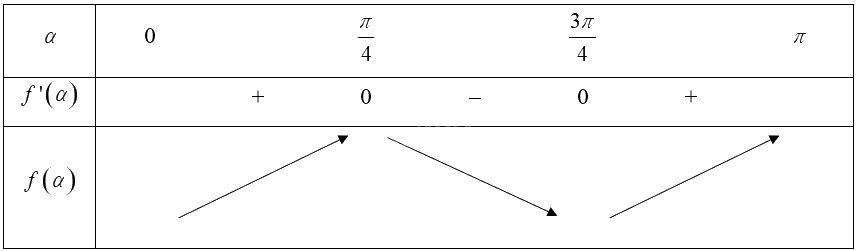
Vậy hàm số đồng biến trên các khoảng \(\left( {0;\frac{\pi }{4}} \right)\) và \(\left( {\frac{{3\pi }}{4};\pi } \right)\), hàm số nghịch biến trên khoảng \(\left( {\frac{\pi }{4};\frac{{3\pi }}{4}} \right)\).
Vậy diện tích hình chữ nhật tăng trên các khoảng \(\left( {0;\frac{\pi }{4}} \right)\) và \(\left( {\frac{{3\pi }}{4};\pi } \right)\), diện tích hình chữ nhật giảm trên khoảng \(\left( {\frac{\pi }{4};\frac{{3\pi }}{4}} \right)\).
Bài 12 trang 12 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Việc nắm vững các công thức đạo hàm cơ bản và kỹ năng tính đạo hàm là yếu tố then chốt để hoàn thành bài tập này một cách hiệu quả.
Bài 12 trang 12 sách bài tập Toán 12 Chân trời sáng tạo thường bao gồm các dạng bài tập sau:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào phân tích từng phần của bài tập. Giả sử bài tập yêu cầu tính đạo hàm của hàm số f(x) = x2 + 2x - 1 tại điểm x = 1.
Vậy, đạo hàm của hàm số f(x) = x2 + 2x - 1 tại điểm x = 1 là 4.
Ngoài bài tập tính đạo hàm tại một điểm, bài 12 trang 12 còn có thể yêu cầu học sinh tìm đạo hàm của các hàm số phức tạp hơn. Trong trường hợp này, cần vận dụng các quy tắc đạo hàm như quy tắc tích, quy tắc thương, quy tắc chuỗi để giải quyết bài toán.
Ví dụ, để tính đạo hàm của hàm số y = (x2 + 1) * sin(x), ta cần sử dụng quy tắc tích:
y' = (x2 + 1)' * sin(x) + (x2 + 1) * (sin(x))' = 2x * sin(x) + (x2 + 1) * cos(x)
Đạo hàm có rất nhiều ứng dụng trong thực tế, chẳng hạn như:
Bài 12 trang 12 sách bài tập Toán 12 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Hy vọng với lời giải chi tiết và các phương pháp giải được trình bày trong bài viết này, các bạn học sinh sẽ tự tin hơn khi giải quyết các bài tập tương tự.
| Công thức | Mô tả |
|---|---|
| (xn)' | Đạo hàm của x mũ n |
| (u + v)' | Đạo hàm của tổng hai hàm số |
| (u * v)' | Đạo hàm của tích hai hàm số |
| Bảng tổng hợp các công thức đạo hàm cơ bản | |