Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 1 trang 31 sách bài tập Toán 12 Chân trời sáng tạo. Bài viết này cung cấp phương pháp giải, đáp án chính xác và giải thích rõ ràng từng bước để giúp học sinh hiểu sâu kiến thức và tự tin làm bài tập.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 12 Chân trời sáng tạo, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
Khảo sát và vẽ đồ thị của các hàm số sau: a) (y = xleft( {{x^2} - 4x} right)); b) (y = - {x^3} + 3{x^2} - 2).
Đề bài
Khảo sát và vẽ đồ thị của các hàm số sau:
a) \(y = x\left( {{x^2} - 4x} \right)\);
b) \(y = - {x^3} + 3{x^2} - 2\).
Phương pháp giải - Xem chi tiết
Sơ đồ khảo sát hàm số:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Xét sự biến thiên của hàm số
‒ Tìm đạo hàm \(y'\), xét dấu \(y'\), xác định khoảng đơn điệu, cực trị (nếu có) của hàm số.
‒ Tìm giới hạn tại vô cực, giới hạn vô cực của hàm số và tìm các đường tiệm cận của đồ thị hàm số (nếu có).
‒ Lập bảng biến thiên của hàm số.
Bước 3. Vẽ đồ thị hàm số
‒ Xác định các điểm cực trị (nếu có), giao điểm của đồ thị với các trục toạ độ (nếu có và dễ tìm),…
‒ Vẽ các đường tiệm cận của đồ thị hàm số (nếu có).
‒ Vẽ đồ thị hàm số.
Lời giải chi tiết
a) \(y = x\left( {{x^2} - 4x} \right) = {x^3} - 4{x^2}\)
1. Tập xác định: \(\mathbb{R}\).
2. Sự biến thiên:
• Chiều biến thiên:
Đạo hàm \(y' = 3{{\rm{x}}^2} - 8{\rm{x}};y' = 0 \Leftrightarrow x = 0\) hoặc \({\rm{x}} = \frac{8}{3}\).
Trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {\frac{8}{3}; + \infty } \right)\), \(y' > 0\) nên hàm số đồng biến trên mỗi khoảng đó.
Trên khoảng \(\left( {0;\frac{8}{3}} \right)\), \(y' < 0\) nên hàm số nghịch biến trên khoảng đó.
• Cực trị:
Hàm số đạt cực đại tại \(x = 0\) và ${{y}_{CĐ}}=0$.
Hàm số đạt cực tiểu tại \(x = \frac{8}{3}\) và \({y_{CT}} = - \frac{{256}}{{27}}\).
• Các giới hạn tại vô cực:
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } {x^3}\left( {1 - \frac{4}{x}} \right) = - \infty ;\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } {x^3}\left( {1 - \frac{4}{x}} \right) = + \infty \).
• Bảng biến thiên:
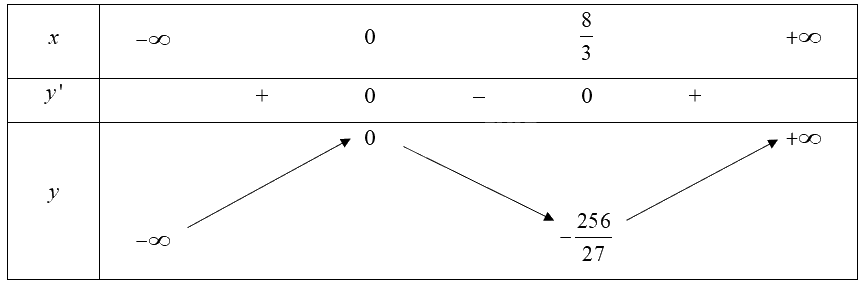
3. Đồ thị
Khi \(x = 0\) thì \(y = 0\) nên \(\left( {0;0} \right)\) là giao điểm của đồ thị với trục \(Oy\).
Ta có \(y = 0 \Leftrightarrow {x^3} - 4{{\rm{x}}^2} = 0 \Leftrightarrow x = 0\) hoặc \({\rm{x}} = 4\).
Vậy đồ thị hàm số giao với trục \(Ox\) tại hai điểm \(\left( {0;0} \right)\) và \(\left( {4;0} \right)\).
Điểm \(\left( {0;0} \right)\) là điểm cực đại và điểm \(\left( {\frac{8}{3}; - \frac{{256}}{{27}}} \right)\) là điểm cực tiểu của đồ thị hàm số.
Vậy đồ thị hàm số được biểu diễn như hình vẽ bên.
Đồ thị của hàm số có tâm đối xứng là điểm \(I\left( {\frac{4}{3}; - \frac{{128}}{{27}}} \right)\).
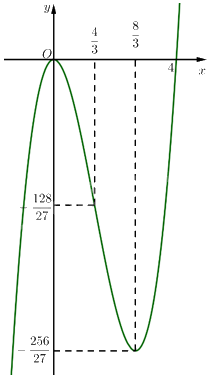
b) \(y = - {x^3} + 3{x^2} - 2\)
1. Tập xác định: \(\mathbb{R}\).
2. Sự biến thiên:
• Chiều biến thiên:
Đạo hàm \(y' = - 3{{\rm{x}}^2} + 6{\rm{x}};y' = 0 \Leftrightarrow x = 0\) hoặc \({\rm{x}} = 2\).
Trên khoảng \(\left( {0;2} \right)\), \(y' > 0\) nên hàm số đồng biến trên khoảng đó.
Trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\), \(y' < 0\) nên hàm số nghịch biến trên mỗi khoảng đó.
• Cực trị:
Hàm số đạt cực đại tại \(x = 2\) và ${{y}_{CĐ}}=4$.
Hàm số đạt cực tiểu tại \(x = 0\) và \({y_{CT}} = 0\).
• Các giới hạn tại vô cực:
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } {x^3}\left( { - 1 + \frac{3}{x} - \frac{2}{{{x^3}}}} \right) = + \infty ;\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } {x^3}\left( { - 1 + \frac{3}{x} - \frac{2}{{{x^3}}}} \right) = - \infty \).
• Bảng biến thiên:
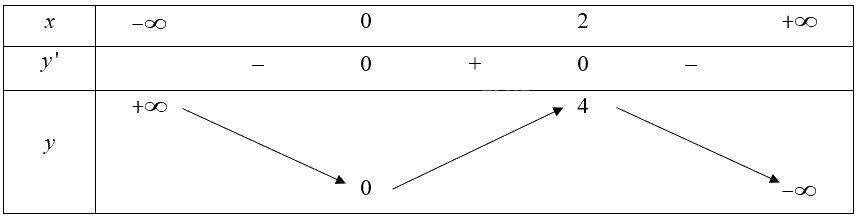
3. Đồ thị
Khi \(x = 0\) thì \(y = 0\) nên \(\left( {0;0} \right)\) là giao điểm của đồ thị với trục \(Oy\).
Ta có \(y = 0 \Leftrightarrow - {x^3} + 3{{\rm{x}}^2} = 0 \Leftrightarrow x = 0\) hoặc \({\rm{x}} = 3\).
Vậy đồ thị hàm số giao với trục \(Ox\) tại hai điểm \(\left( {0;0} \right)\) và \(\left( {3;0} \right)\).
Điểm \(\left( {2;4} \right)\) là điểm cực đại và điểm \(\left( {0;0} \right)\) là điểm cực tiểu của đồ thị hàm số.
Vậy đồ thị hàm số được biểu diễn như hình vẽ bên.
Đồ thị của hàm số có tâm đối xứng là điểm \(I\left( {2;2} \right)\).
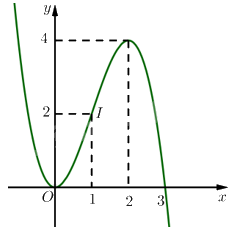
Bài 1 trang 31 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng các định nghĩa, tính chất của giới hạn để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập là rất quan trọng để đạt kết quả tốt trong các kỳ thi sắp tới.
Bài 1 trang 31 sách bài tập Toán 12 Chân trời sáng tạo thường bao gồm các dạng bài tập sau:
Để giải bài tập về giới hạn hàm số, học sinh cần nắm vững các phương pháp sau:
Câu a: Tính giới hạn lim (x→2) (x^2 - 4) / (x - 2)
Giải:
Ta có: lim (x→2) (x^2 - 4) / (x - 2) = lim (x→2) (x - 2)(x + 2) / (x - 2) = lim (x→2) (x + 2) = 2 + 2 = 4
Câu b: Tính giới hạn lim (x→∞) (2x + 1) / (x - 3)
Giải:
Ta có: lim (x→∞) (2x + 1) / (x - 3) = lim (x→∞) (2 + 1/x) / (1 - 3/x) = (2 + 0) / (1 - 0) = 2
Để học tập và ôn luyện kiến thức về giới hạn hàm số, học sinh có thể tham khảo các tài liệu sau:
Bài 1 trang 31 sách bài tập Toán 12 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về giới hạn hàm số. Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trong bài viết này, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong các kỳ thi.