Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12 sách Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn giải bài 7 trang 46 một cách đầy đủ và chính xác.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Một kĩ sư xây dựng thiết kế khung một ngôi nhà trong không gian (Oxyz) như Hình 9 nhờ một phần mềm đồ hoạ máy tính. a) Viết phương trình mặt phẳng mái nhà (left( {DEMM} right)). b) Tính khoảng cách từ điểm (B) đến mái nhà (left( {DEMM} right)).
Đề bài
Một kĩ sư xây dựng thiết kế khung một ngôi nhà trong không gian \(Oxyz\) như Hình 9 nhờ một phần mềm đồ hoạ máy tính.
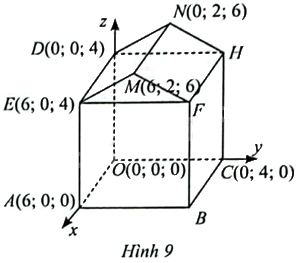
a) Viết phương trình mặt phẳng mái nhà \(\left( {DEMM} \right)\).
b) Tính khoảng cách từ điểm \(B\) đến mái nhà \(\left( {DEMM} \right)\).
Phương pháp giải - Xem chi tiết
Lập phương trình tổng quát của mặt phẳng đi qua ba điểm không thẳng hàng \(A,B,C\):
Bước 1: Tìm cặp vectơ chỉ phương, chẳng hạn \(\overrightarrow {AB} ,\overrightarrow {AC} \).
Bước 2: Tìm một vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\).
Bước 3: Viết phương trình mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(A\) và có vectơ pháp tuyến \(\overrightarrow n \).
‒ Khoảng cách từ điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng \(\left( P \right):Ax + By + C{\rm{z}} + D = 0\):
$d\left( {{M}_{0}};\left( P \right) \right)=\frac{\left| A{{x}_{0}}+B{{y}_{0}}+C{{\text{z}}_{0}}+D \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}+{{C}^{2}}}}$.
Lời giải chi tiết
a) Ta có: \(\overrightarrow {DE} = \left( {6;0;0} \right),\overrightarrow {DN} = \left( {0;2;2} \right)\).
Khi đó, \(\left[ {\overrightarrow {DE} ,\overrightarrow {DN} } \right] = \left( {0.2 - 0.2;0.0 - 6.2;6.2 - 0.0} \right) = \left( {0; - 12;12} \right)\) là vectơ pháp tuyến của mặt phẳng \(\left( {DEMM} \right)\).
Phương trình mặt phẳng \(\left( {DEMM} \right)\) là:
\(0\left( {x - 0} \right) - 12\left( {y - 0} \right) + 12\left( {z - 4} \right) = 0 \Leftrightarrow - 12y + 12{\rm{z}} - 48 = 0 \Leftrightarrow y - z + 4 = 0\).
b) \(OABC.DEFH\) là hình hộp chữ nhật nên \(B\left( {6;4;0} \right)\)
Khoảng cách từ điểm \(B\) đến mái nhà \(\left( {DEMM} \right)\) bằng:
\(d\left( {B,\left( {DEMM} \right)} \right) = \frac{{\left| {4 - 0 + 4} \right|}}{{\sqrt {{0^2} + {1^2} + {{\left( { - 1} \right)}^2}} }} = 4\sqrt 2 \).
Bài 7 trang 46 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, đạo hàm của tổng, hiệu, tích, thương của các hàm số, và quy tắc đạo hàm của hàm hợp để giải quyết các bài toán cụ thể.
Bài 7 thường bao gồm các dạng bài tập sau:
Để giải bài 7 trang 46 một cách hiệu quả, bạn cần nắm vững các kiến thức và kỹ năng sau:
Ví dụ: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Giải:
f'(x) = (x3)' + (2x2)' - (5x)' + (1)'
f'(x) = 3x2 + 4x - 5 + 0
f'(x) = 3x2 + 4x - 5
Khi giải bài 7 trang 46, bạn cần lưu ý những điều sau:
Để củng cố kiến thức và kỹ năng giải bài 7 trang 46, bạn có thể làm thêm các bài tập tương tự sau:
Bài 7 trang 46 sách bài tập Toán 12 Chân trời sáng tạo là một bài tập quan trọng giúp bạn củng cố kiến thức về đạo hàm. Hy vọng rằng với hướng dẫn chi tiết và các ví dụ minh họa trong bài viết này, bạn sẽ giải quyết bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tốt!