Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài tập 8 trang 80 sách bài tập Toán 12 - Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt kết quả cao trong môn Toán.
Một công ty bảo hiểm ô tô nhận thấy nếu một tài xế gặp sự cố trong một năm thì xác suất gặp sự cố ở năm tiếp theo là 0,2; còn nếu trong một năm không gặp sự cố nào thì xác suất gặp sự cố ở năm tiếp theo là 0,05. Xác suất để một tài xế gặp sự cố ở năm đầu tiên lái xe là 0,1. Sử dụng sơ đồ hình cây: a) Tính xác suất để một tài xế không gặp sự cố nào trong 2 năm đầu tiên lái xe. b) Tính xác suất để một tài xế gặp sự cố trong cả 2 năm đầu tiên lái xe. Làm tròn kết quả đến hàng phần trăm.
Đề bài
Một công ty bảo hiểm ô tô nhận thấy nếu một tài xế gặp sự cố trong một năm thì xác suất gặp sự cố ở năm tiếp theo là 0,2; còn nếu trong một năm không gặp sự cố nào thì xác suất gặp sự cố ở năm tiếp theo là 0,05. Xác suất để một tài xế gặp sự cố ở năm đầu tiên lái xe là 0,1. Sử dụng sơ đồ hình cây:
a) Tính xác suất để một tài xế không gặp sự cố nào trong 2 năm đầu tiên lái xe.
b) Tính xác suất để một tài xế gặp sự cố trong cả 2 năm đầu tiên lái xe. Làm tròn kết quả đến hàng phần trăm.
Phương pháp giải - Xem chi tiết
Sử dụng sơ đồ hình cây.
Lời giải chi tiết
Gọi \(A\) là biến cố “Tài xế không gặp sự cố trong năm đầu tiên lái xe”, \(B\) là biến cố “Tài xế không gặp sự cố trong năm thứ hai lái xe”.
Xác suất để một tài xế gặp sự cố ở năm đầu tiên lái xe là 0,1 nên ta có \(P\left( {\overline A } \right) = 0,1\).
Do đó \(P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - 0,1 = 0,9\).
Nếu một tài xế gặp sự cố trong một năm thì xác suất gặp sự cố ở năm tiếp theo là 0,2 nên ta có \(P\left( {\overline B |\overline A } \right) = 0,2\).
Do đó \(P\left( {B|\overline A } \right) = 1 - P\left( {\overline B |\overline A } \right) = 1 - 0,2 = 0,8\).
Nếu trong một năm không gặp sự cố nào thì xác suất gặp sự cố ở năm tiếp theo là 0,05 nên ta có \(P\left( {\overline B |A} \right) = 0,05\).
Do đó \(P\left( {B|A} \right) = 1 - P\left( {\overline B |A} \right) = 1 - 0,05 = 0,95\).
Ta có sơ đồ hình cây như sau:
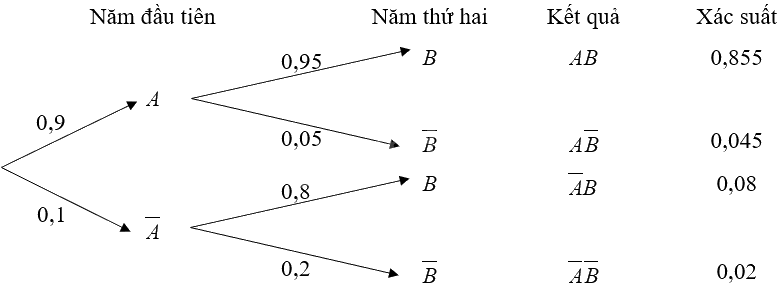
a) Xác suất để một tài xế không gặp sự cố nào trong 2 năm đầu tiên lái xe là: \(P\left( {AB} \right) = 0,855\).
b) Xác suất để một tài xế gặp sự cố trong cả 2 năm đầu tiên lái xe là \(P\left( {\overline A \overline B } \right) = 0,02\).
Bài tập 8 trang 80 sách bài tập Toán 12 - Chân trời sáng tạo thuộc chương trình học về đạo hàm. Bài tập này thường tập trung vào việc vận dụng các quy tắc tính đạo hàm của hàm số, đặc biệt là đạo hàm của hàm hợp và đạo hàm của hàm lượng giác. Việc nắm vững kiến thức về đạo hàm là nền tảng quan trọng để giải quyết các bài toán liên quan đến cực trị, điểm uốn và ứng dụng của đạo hàm trong các lĩnh vực khác.
Bài tập 8 thường bao gồm các dạng bài sau:
Để giải quyết hiệu quả bài tập 8 trang 80, bạn có thể áp dụng các phương pháp sau:
Bài toán: Tính đạo hàm của hàm số y = sin(x2 + 1).
Giải:
Áp dụng quy tắc hàm hợp, ta có:
y' = cos(x2 + 1) * (x2 + 1)' = cos(x2 + 1) * 2x = 2x * cos(x2 + 1).
Khi giải bài tập về đạo hàm, bạn cần lưu ý những điều sau:
Để học tập và ôn luyện kiến thức về đạo hàm, bạn có thể tham khảo các tài liệu sau:
Bài tập 8 trang 80 sách bài tập Toán 12 - Chân trời sáng tạo là một bài tập quan trọng giúp bạn củng cố kiến thức về đạo hàm. Hy vọng với những hướng dẫn và ví dụ minh họa trên, bạn sẽ giải quyết bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tập tốt!