Bài 3 trang 33 sách bài tập Toán 12 Chân trời sáng tạo là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn của hàm số để giải quyết các bài toán cụ thể.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ {0;4} \right]\) trong Hình 1 là: A. ‒1. B. ‒2. C. 0. D. 1.
Đề bài
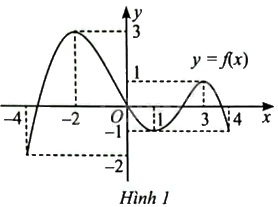
Giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ {0;4} \right]\) trong Hình 1 là:
A. ‒1.
B. ‒2.
C. 0.
D. 1.
Phương pháp giải - Xem chi tiết
Dựa vào đồ thị hàm số.
Lời giải chi tiết
Dựa vào đồ thị ta có: \(\mathop {\min }\limits_{\left[ {0;4} \right]} f\left( x \right) = f\left( 1 \right) = f\left( 4 \right) = - 1\).
Chọn A.
Bài 3 trang 33 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học về giới hạn của hàm số. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản về giới hạn, các định lý liên quan và các phương pháp tính giới hạn thường gặp.
Bài tập yêu cầu tính giới hạn của hàm số tại một điểm cho trước. Cụ thể, hàm số có thể là hàm đa thức, hàm hữu tỉ, hoặc hàm lượng giác. Việc xác định đúng dạng hàm số và áp dụng phương pháp tính giới hạn phù hợp là yếu tố then chốt để giải quyết bài tập này.
Có nhiều phương pháp để tính giới hạn của hàm số, tùy thuộc vào dạng hàm số. Một số phương pháp thường được sử dụng bao gồm:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi xin trình bày lời giải chi tiết như sau:
(a) Giới hạn của hàm số f(x) = (x^2 - 1) / (x - 1) khi x tiến tới 1.
Ta có thể phân tích tử số thành nhân tử: x^2 - 1 = (x - 1)(x + 1). Do đó, f(x) = [(x - 1)(x + 1)] / (x - 1) = x + 1 (với x ≠ 1).
Vậy, lim (x→1) f(x) = lim (x→1) (x + 1) = 1 + 1 = 2.
(b) Giới hạn của hàm số g(x) = (x^3 + 8) / (x + 2) khi x tiến tới -2.
Ta có thể phân tích tử số thành nhân tử: x^3 + 8 = (x + 2)(x^2 - 2x + 4). Do đó, g(x) = [(x + 2)(x^2 - 2x + 4)] / (x + 2) = x^2 - 2x + 4 (với x ≠ -2).
Vậy, lim (x→-2) g(x) = lim (x→-2) (x^2 - 2x + 4) = (-2)^2 - 2(-2) + 4 = 4 + 4 + 4 = 12.
Khi giải bài tập về giới hạn, học sinh cần lưu ý một số điểm sau:
Kiến thức về giới hạn có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và khoa học kỹ thuật, bao gồm:
Bài 3 trang 33 sách bài tập Toán 12 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về giới hạn của hàm số. Hy vọng với lời giải chi tiết và các lưu ý trên, các bạn học sinh sẽ tự tin hơn trong quá trình học tập và giải quyết các bài toán tương tự.