Bài 9 trang 64 sách bài tập Toán 12 Chân trời sáng tạo là một bài tập quan trọng trong chương trình học. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài 9 trang 64, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
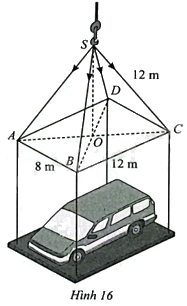
Tính độ lớn của các lực căng trên mỗi sợi dây cáp trong Hình 16. Cho biết khối lượng xe là 1900 kg, gia tốc là 10 m/s, khung nâng có khối lượng 100 kg và có dạng hình chóp \(S.ABCD\) với đáy \(ABCD\) là hình chữ nhật tâm \(O\), \(AB=8m,BC=12m,SC=12m\) và \(SO\) vuông góc với \(\left( {ABCD} \right)\). Làm tròn kết quả đến hàng đơn vị của Newton.
Đề bài
Tính độ lớn của các lực căng trên mỗi sợi dây cáp trong Hình 16. Cho biết khối lượng xe là 1900 kg, gia tốc là 10 m/s, khung nâng có khối lượng 100 kg và có dạng hình chóp \(S.ABCD\) với đáy \(ABCD\) là hình chữ nhật tâm \(O\), \(AB=8m,BC=12m,SC=12m\) và \(SO\) vuông góc với \(\left( {ABCD} \right)\). Làm tròn kết quả đến hàng đơn vị của Newton.
Phương pháp giải - Xem chi tiết
‒ Sử dụng định lí Pitago và lượng giác.
‒ Công thức tính độ lớn trọng lực: \(P = m.g\).
Lời giải chi tiết
\(\begin{array}{l}AC = B{\rm{D}} = \sqrt {A{B^2} + B{C^2}} = \sqrt {{8^2} + {{12}^2}} = 4\sqrt {13} \\OC = \frac{1}{2}AC = 2\sqrt {13} ;SO = \sqrt {S{C^2} - O{C^2}} = \sqrt {{{12}^2} - {{\left( {2\sqrt {13} } \right)}^2}} = 2\sqrt {23} \\\sin \widehat {SCO} = \frac{{SO}}{{SC}} = \frac{{2\sqrt {23} }}{{12}} = \frac{{\sqrt {23} }}{6}\end{array}\)
Gọi \(P\) là độ lớn của trọng lực xe và khung sắt nâng, \(F\) là độ lớn của lực căng trên mỗi sợi cáp.
Ta có \(P = \left( {1900 + 100} \right).10 = 20000\left( N \right)\)
\(F\sin \widehat {SCO} = \frac{P}{4} \Rightarrow F = \frac{P}{{4\sin \widehat {SCO}}} = \frac{{20000}}{{4.\frac{{\sqrt {23} }}{6}}} \approx 6255\left( N \right)\).
Bài 9 trang 64 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Dưới đây là hướng dẫn giải chi tiết bài 9 trang 64 sách bài tập Toán 12 Chân trời sáng tạo:
(Giả định đề bài: Cho hàm số y = f(x) có đạo hàm f'(x) = 3x2 - 6x + 1. Tìm điểm cực trị của hàm số.)
Để tìm điểm cực trị của hàm số, ta cần thực hiện các bước sau:
Bước 1: Tập xác định của hàm số là R (vì hàm số là hàm đa thức).
Bước 2: Đạo hàm của hàm số là f'(x) = 3x2 - 6x + 1.
Bước 3: Giải phương trình f'(x) = 0:
3x2 - 6x + 1 = 0
Sử dụng công thức nghiệm của phương trình bậc hai, ta có:
x = (6 ± √(36 - 4*3*1)) / (2*3) = (6 ± √24) / 6 = (6 ± 2√6) / 6 = 1 ± √6 / 3
Vậy, phương trình có hai nghiệm là x1 = 1 - √6 / 3 và x2 = 1 + √6 / 3.
Bước 4: Xét dấu đạo hàm f'(x) trên các khoảng xác định:
| Khoảng | x < 1 - √6 / 3 | 1 - √6 / 3 < x < 1 + √6 / 3 | x > 1 + √6 / 3 |
|---|---|---|---|
| f'(x) | + | - | + |
| Hàm số | Đồng biến | Nghịch biến | Đồng biến |
Từ bảng xét dấu, ta thấy:
Do đó, hàm số đạt cực đại tại x1 = 1 - √6 / 3 và đạt cực tiểu tại x2 = 1 + √6 / 3.
Giá trị cực đại của hàm số là f(1 - √6 / 3) và giá trị cực tiểu của hàm số là f(1 + √6 / 3). (Việc tính toán giá trị cụ thể của f(x) phụ thuộc vào biểu thức cụ thể của hàm số y = f(x)).
Vậy, hàm số đạt cực đại tại x = 1 - √6 / 3 và đạt cực tiểu tại x = 1 + √6 / 3.
Bài tập này giúp học sinh rèn luyện kỹ năng tính đạo hàm và ứng dụng đạo hàm để tìm điểm cực trị của hàm số. Việc nắm vững kiến thức này là rất quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình Toán 12.
Ngoài ra, học sinh có thể tham khảo thêm các bài giảng và tài liệu học tập khác trên giaitoan.edu.vn để hiểu rõ hơn về đạo hàm và các ứng dụng của nó.