Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 10 trang 22 sách bài tập Toán 12 Chân trời sáng tạo. Bài viết này cung cấp phương pháp giải bài tập một cách rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cập nhật đáp án nhanh chóng và chính xác, đảm bảo hỗ trợ tối đa cho quá trình học tập của bạn. Hãy cùng khám phá lời giải chi tiết ngay sau đây!
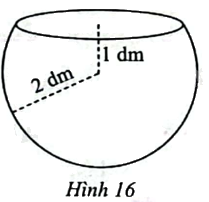
Một bể cá có dạng là một phần hình cầu được tạo thành khi cắt hình cầu bán kính 2 dm bằng mặt phẳng cách tâm của hình cầu 1 dm (Hình 16). Tính dung tích của bể cá (kết quả làm tròn đến hàng phần mười của đềximét khối). Gợi ý: Có thể coi bể cá là khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số (y = sqrt {4 - {x^2}} ) với ( - 2 le x le 1), trục hoành và đường thẳng (x = 1) quanh trục hoành.
Đề bài
Một bể cá có dạng là một phần hình cầu được tạo thành khi cắt hình cầu bán kính 2 dm bằng mặt phẳng cách tâm của hình cầu 1 dm (Hình 16). Tính dung tích của bể cá (kết quả làm tròn đến hàng phần mười của đềximét khối).
Gợi ý: Có thể coi bể cá là khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số \(y = \sqrt {4 - {x^2}} \) với \( - 2 \le x \le 1\), trục hoành và đường thẳng \(x = 1\) quanh trục hoành.
Phương pháp giải - Xem chi tiết
Gắn parabol vào hệ trục toạ độ \(Oxy\), sau đó sử dụng công thức: Tính thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi đồ thị của hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b\) quay quanh trục \(Ox\) là: \(V = \pi \int\limits_a^b {{{\left[ {f\left( x \right)} \right]}^2}dx} \).
Lời giải chi tiết
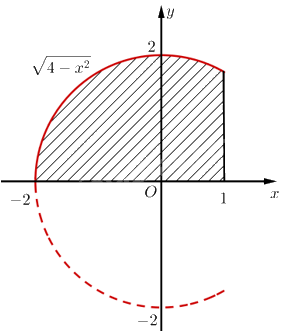
Chọn hệ trục toạ độ \(Oxy\) như hình vẽ.
Coi bể cá là khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số \(y = \sqrt {4 - {x^2}} \) với \( - 2 \le x \le 1\), trục hoành và đường thẳng \(x = 1\) quanh trục hoành.
Dung tích của bể cá là:
\(V = \pi \int\limits_{ - 2}^1 {{{\left( {\sqrt {4 - {x^2}} } \right)}^2}dx} = \pi \int\limits_{ - 2}^1 {\left( {4 - {x^2}} \right)dx} = \left. {\pi \left( {4x - \frac{{{x^3}}}{3}} \right)} \right|_{ - 2}^1 = 9\pi \approx 28,3\left( {d{m^3}} \right)\).
Bài 10 trang 22 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Việc nắm vững các công thức đạo hàm cơ bản và kỹ năng tính đạo hàm là yếu tố then chốt để hoàn thành bài tập này một cách hiệu quả.
Bài 10 trang 22 sách bài tập Toán 12 Chân trời sáng tạo thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi xin trình bày lời giải chi tiết như sau:
Cho hàm số f(x) = x2 + 2x + 1. Tính f'(2).
Giải:
Ta có f'(x) = 2x + 2. Thay x = 2 vào, ta được f'(2) = 2*2 + 2 = 6.
Tìm đạo hàm của hàm số g(x) = sin(x) + cos(x).
Giải:
Ta có g'(x) = cos(x) - sin(x).
| Hàm số | Đạo hàm |
|---|---|
| f(x) = c (hằng số) | f'(x) = 0 |
| f(x) = xn | f'(x) = nxn-1 |
| f(x) = sin(x) | f'(x) = cos(x) |
| f(x) = cos(x) | f'(x) = -sin(x) |
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
Hy vọng với lời giải chi tiết và các kiến thức bổ ích trên, các em học sinh sẽ tự tin hơn khi giải bài 10 trang 22 sách bài tập Toán 12 Chân trời sáng tạo. Chúc các em học tập tốt!