Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 6 trang 105 Sách bài tập Toán 12 - Chân trời sáng tạo. Bài viết này cung cấp đáp án, phương pháp giải và giải thích rõ ràng, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, dễ hiểu và cập nhật mới nhất để hỗ trợ tối đa cho quá trình học tập của bạn.
Chị Yến thống kê lại thời gian chạy cự li 200 m của mình ở một số lần luyện tập trong năm 2022 và 2023 như sau: a) Hãy tính các số đặc trưng đo mức độ phân tán thời gian chạy mỗi năm của chị Yến (kết quả làm tròn đến hàng phần nghìn). b) Độ phân tán của mẫu số liệu cho biết điều gì?
Đề bài
Chị Yến thống kê lại thời gian chạy cự li 200 m của mình ở một số lần luyện tập trong năm 2022 và 2023 như sau:
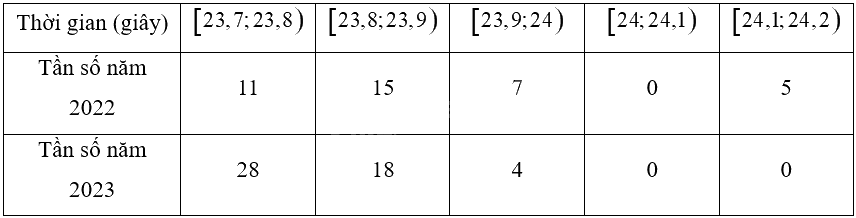
a) Hãy tính các số đặc trưng đo mức độ phân tán thời gian chạy mỗi năm của chị Yến (kết quả làm tròn đến hàng phần nghìn).
b) Độ phân tán của mẫu số liệu cho biết điều gì?
Phương pháp giải - Xem chi tiết
‒ Sử dụng công thức tính khoảng biến thiên của mẫu số liệu ghép nhóm: \(R = {a_{m + 1}} - {a_1}\).
‒ Sử dụng công thức tính các tứ phân vị của mẫu số liệu ghép nhóm:
Tứ phân vị thứ \(k\) được xác định như sau: \({Q_k} = {u_m} + \frac{{\frac{{kn}}{4} - C}}{{{n_m}}}\left( {{u_{m + 1}} - {u_m}} \right)\)
trong đó:
• \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu;
• \(\left[ {{u_m};{u_{m + 1}}} \right)\) là nhóm chứa tứ phân vị thứ \(k\);
• \({n_m}\) là tần số của nhóm chứa tứ phân vị thứ \(k\);
• \(C = {n_1} + {n_2} + ... + {n_{m - 1}}\).
‒ Sử dụng công thức tính khoảng tứ phân vị của mẫu số liệu ghép nhóm: \(\Delta Q = {Q_3} - {Q_1}\).
‒ Sử dụng công thức tính phương sai của mẫu số liệu ghép nhóm:
\(\begin{array}{l}{S^2} = \frac{1}{n}\left[ {{n_1}{{\left( {{c_1} - \overline x } \right)}^2} + {n_2}{{\left( {{c_2} - \overline x } \right)}^2} + ... + {n_k}{{\left( {{c_k} - \overline x } \right)}^2}} \right]\\ & = \frac{1}{n}\left[ {{n_1}c_1^2 + {n_2}c_2^2 + ... + {n_k}c_k^2} \right] - {\overline x ^2}\end{array}\)
Lời giải chi tiết
a) Ta có bảng sau:
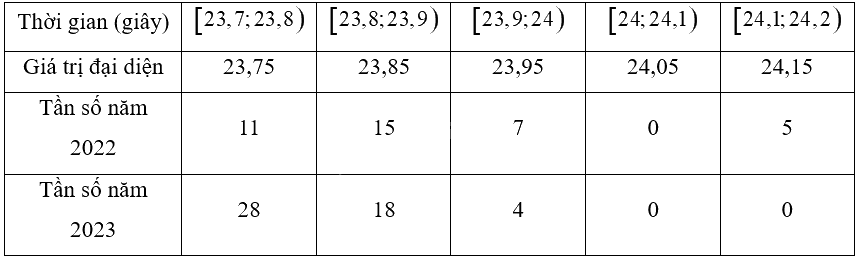
*Mẫu số liệu năm 2022:
Khoảng biến thiên của thời gian chạy cự li 200 m của chị Yến trong năm 2022 là:
\({R_A} = 24,2 - 23,7 = 0,5\) (giây).
• Tứ phân vị của thời gian chạy cự li 200 m của chị Yến trong năm 2022:
\({n_A} = 11 + 15 + 7 + 0 + 5 = 38\)
Gọi \({x_1};{x_2};...;{x_{38}}\) là mẫu số liệu gốc gồm thời gian chạy cự li 200 m trong 38 lần luyện tập của chị Yến trong năm 2022 theo thứ tự không giảm.
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({x_{10}} \in \left[ {23,7;23,8} \right)\). Do đó tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
\({Q_{A1}} = 23,7 + \frac{{\frac{{1.38}}{4} - 0}}{{11}}\left( {23,8 - 23,7} \right) = \frac{{5233}}{{220}}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{29}} \in \left[ {23,9;24} \right)\). Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
\({Q_{A3}} = 23,9 + \frac{{\frac{{3.38}}{4} - \left( {11 + 15} \right)}}{7}\left( {24 - 23,9} \right) = \frac{{3351}}{{140}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
\(\Delta {Q_A} = {Q_{A3}} - {Q_{A1}} = \frac{{3351}}{{140}} - \frac{{5233}}{{220}} \approx 0,15\) (giây).
• Phương sai và độ lệch chuẩn của cân nặng của các trái cam thu hoạch năm 2022:
Cỡ mẫu \({n_A} = 38\)
Số trung bình của mẫu số liệu ghép nhóm là:
\(\overline {{x_A}} = \frac{{11.23,75 + 15.23,85 + 7.23,95 + 5.24,15}}{{38}} = \frac{{4537}}{{190}}\)
Phương sai của mẫu số liệu ghép nhóm đó là:
\(S_A^2 = \frac{1}{{38}}\left( {{{11.23,75}^2} + {{15.23,85}^2} + {{7.23,95}^2} + {{5.24,15}^2}} \right) - {\left( {\frac{{4537}}{{190}}} \right)^2} \approx 0,016\)
Độ lệch chuẩn của mẫu số liệu ghép nhóm đó là: \({S_A} \approx \sqrt {0,016} \approx 0,126\).
*Mẫu số liệu năm 2023:
Khoảng biến thiên của thời gian chạy cự li 200 m của chị Yến trong năm 2023 là:
\({R_B} = 24 - 23,7 = 0,3\) (giây).
• Tứ phân vị của thời gian chạy cự li 200 m của chị Yến trong năm 2023:
\({n_B} = 28 + 18 + 4 = 50\)
Gọi \({x_1};{x_2};...;{x_{50}}\) là mẫu số liệu gốc gồm thời gian chạy cự li 200 m trong 50 lần luyện tập của chị Yến trong năm 2023 theo thứ tự không giảm.
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({x_{13}} \in \left[ {23,7;23,8} \right)\). Do đó tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
\({Q_{B1}} = 23,7 + \frac{{\frac{{1.50}}{4} - 0}}{{28}}\left( {23,8 - 23,7} \right) = \frac{{13297}}{{560}}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{38}} \in \left[ {23,8;23,9} \right)\). Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
\({Q_{B3}} = 23,8 + \frac{{\frac{{3.50}}{4} - 28}}{{18}}\left( {23,9 - 23,8} \right) = \frac{{8587}}{{360}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
\(\Delta {Q_B} = {Q_{B3}} - {Q_{B1}} = \frac{{8587}}{{360}} - \frac{{13297}}{{560}} = \frac{{109}}{{1008}} \approx 0,11\) (giây).
• Phương sai và độ lệch chuẩn của cân nặng của các trái cam thu hoạch năm 2022:
Cỡ mẫu \({n_B} = 50\)
Số trung bình của mẫu số liệu ghép nhóm là:
\(\overline {{x_B}} = \frac{{28.23,75 + 18.23,85 + 4.23,95}}{{50}} = \frac{{11901}}{{500}}\)
Phương sai của mẫu số liệu ghép nhóm đó là:
\(S_B^2 = \frac{1}{{50}}\left( {{{28.23,75}^2} + {{18.23,85}^2} + {{4.23,95}^2}} \right) - {\left( {\frac{{11901}}{{500}}} \right)^2} \approx 0,004\)
Độ lệch chuẩn của mẫu số liệu ghép nhóm đó là: \({S_B} \approx \sqrt {0,004} \approx 0,063\).
b) Nếu so sánh theo khoảng biến thiên, theo khoảng tứ phân vị hoặc theo phương sai, độ lệch chuẩn thì ta luôn có thời gian chạy năm 2023 đồng đều hơn thời gian chạy năm 2022.
Bài 6 trang 105 Sách bài tập Toán 12 - Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về các chủ đề đã học. Bài tập này thường yêu cầu học sinh vận dụng các công thức, định lý và kỹ năng giải toán đã được trang bị để giải quyết các bài toán thực tế.
Bài 6 thường bao gồm các dạng bài tập sau:
Để giải quyết các bài toán về đạo hàm, học sinh cần nắm vững các công thức tính đạo hàm của các hàm số cơ bản, các quy tắc tính đạo hàm và các ứng dụng của đạo hàm như tìm cực trị, khảo sát hàm số, giải phương trình, bất phương trình.
Ví dụ:
Cho hàm số y = x3 - 3x2 + 2. Tìm cực trị của hàm số.
Giải:
Để giải quyết các bài toán về tích phân, học sinh cần nắm vững các công thức tính tích phân, các phương pháp tính tích phân và các ứng dụng của tích phân như tính diện tích hình phẳng, tính thể tích vật thể.
Ví dụ:
Tính tích phân ∫01 x2 dx.
Giải:
∫01 x2 dx = [x3/3]01 = (13/3) - (03/3) = 1/3.
Để giải quyết các bài toán về số phức, học sinh cần nắm vững các khái niệm về số phức, các phép toán trên số phức và các ứng dụng của số phức.
Để giải quyết các bài toán về hình học không gian, học sinh cần nắm vững các khái niệm về hình học không gian, các công thức tính diện tích, thể tích và các phương pháp giải toán hình học không gian.
Bài 6 trang 105 Sách bài tập Toán 12 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Hy vọng với hướng dẫn chi tiết này, các bạn học sinh sẽ tự tin hơn khi giải bài tập và đạt kết quả tốt trong môn Toán.