Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 4 trang 104 sách bài tập Toán 12 Chân trời sáng tạo. Bài viết này cung cấp phương pháp giải, đáp án chính xác và giải thích rõ ràng từng bước để giúp học sinh hiểu sâu kiến thức và tự tin làm bài tập.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 12, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
Bác Xuân biểu diễn thời gian tập thể dục mỗi ngày của mình trong 120 ngày liên tiếp ở biểu đồ tần số tương đối ghép nhóm dưới đây. a) Lập bảng tần số ghép nhóm cho dữ liệu ở biểu đồ trên. b) Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần trăm).
Đề bài
Bác Xuân biểu diễn thời gian tập thể dục mỗi ngày của mình trong 120 ngày liên tiếp ở biểu đồ tần số tương đối nghép nhóm dưới đây.
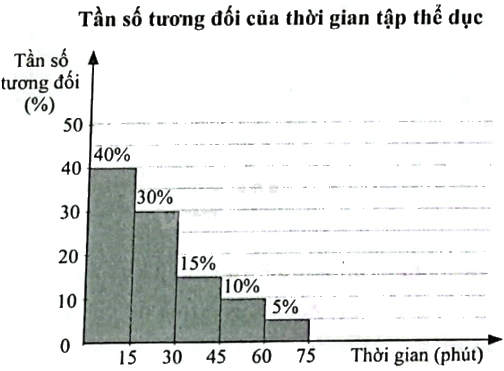
a) Lập bảng tần số ghép nhóm cho dữ liệu ở biểu đồ trên.
b) Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần trăm).
Phương pháp giải - Xem chi tiết
‒ Sử dụng công thức tính phương sai của mẫu số liệu ghép nhóm:
\(\begin{array}{l}{S^2} = \frac{1}{n}\left[ {{n_1}{{\left( {{c_1} - \overline x } \right)}^2} + {n_2}{{\left( {{c_2} - \overline x } \right)}^2} + ... + {n_k}{{\left( {{c_k} - \overline x } \right)}^2}} \right]\\ & = \frac{1}{n}\left[ {{n_1}c_1^2 + {n_2}c_2^2 + ... + {n_k}c_k^2} \right] - {\overline x ^2}\end{array}\)
‒ Sử dụng công thức tính độ lệch chuẩn của mẫu số liệu ghép nhóm: \(S = \sqrt {{S^2}} \).
Lời giải chi tiết
a) Ta có bảng tần số ghép nhóm:

b) Ta có bảng sau:

Cỡ mẫu \(n = 48 + 36 + 18 + 12 + 6 = 120\)
Số trung bình của mẫu số liệu ghép nhóm là:
\(\overline x = \frac{{48.7,5 + 36.22,5 + 18.37,5 + 12.52,5 + 6.67,5}}{{120}} = 24\)
Phương sai của mẫu số liệu ghép nhóm đó là:
\({S^2} = \frac{1}{{120}}\left( {{{48.7,5}^2} + {{36.22,5}^2} + {{18.37,5}^2} + {{12.52,5}^2} + {{6.67,5}^2}} \right) - {24^2} = 312,75\)
Độ lệch chuẩn của mẫu số liệu ghép nhóm là: \(S = \sqrt {312,75} \approx 17,68\).
Bài 4 trang 104 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, đạo hàm của tổng, hiệu, tích, thương của các hàm số, và quy tắc đạo hàm của hàm hợp để giải quyết các bài toán cụ thể.
Bài 4 thường bao gồm các dạng bài tập sau:
Để giải bài 4 trang 104 sách bài tập Toán 12 Chân trời sáng tạo hiệu quả, học sinh cần nắm vững các kiến thức và kỹ năng sau:
Ví dụ: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Giải:
f'(x) = (x3)' + (2x2)' - (5x)' + (1)'
f'(x) = 3x2 + 4x - 5 + 0
f'(x) = 3x2 + 4x - 5
Trong quá trình giải bài tập, học sinh cần lưu ý những điều sau:
Để học tập và ôn luyện kiến thức về đạo hàm, học sinh có thể tham khảo các tài liệu sau:
Bài 4 trang 104 sách bài tập Toán 12 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Bằng cách nắm vững các kiến thức và kỹ năng cần thiết, học sinh có thể tự tin giải quyết các bài toán liên quan đến đạo hàm một cách hiệu quả.