Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12 sách Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 4 trang 76, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Cho hình hộp \(ABCD.A'B'C'D'\) có \(A\left( {2;4;0} \right),B\left( {4;0;0} \right),C\left( { - 1;4; - 7} \right)\) và \(D'\left( {6;8;10} \right)\). Tìm toạ độ của điểm \(B'\).
Đề bài
Cho hình hộp \(ABCD.A'B'C'D'\) có \(A\left( {2;4;0} \right),B\left( {4;0;0} \right),C\left( { - 1;4; - 7} \right)\) và \(D'\left( {6;8;10} \right)\). Tìm toạ độ của điểm \(B'\).
Phương pháp giải - Xem chi tiết
‒ Sử dụng toạ độ của vectơ \(\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A}} \right)\).
‒ Sử dụng tính chất hai vectơ bằng nhau: Với \(\overrightarrow u = \left( {{x_1};{y_1};{z_1}} \right)\) và \(\overrightarrow v = \left( {{x_2};{y_2};{z_2}} \right)\), ta có: \(\overrightarrow u = \overrightarrow v \Leftrightarrow \left\{ \begin{array}{l}{x_1} = {x_2}\\{y_1} = {y_2}\\{z_1} = {z_2}\end{array} \right.\).
Lời giải chi tiết
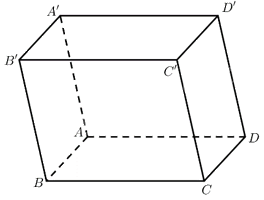
Giả sử \(D\left( {{x_D};{y_D};{z_D}} \right)\). Ta có
\(\overrightarrow {AD} = \left( {{x_D} - 2;{y_D} - 4;{z_D}} \right)\).
\(\overrightarrow {BC} = \left( { - 1 - 4;4 - 0; - 7 - 0} \right) = \left( { - 5;4; - 7} \right)\).
\(ABCD\) là hình bình hành nên \(\overrightarrow {AD} = \overrightarrow {BC} \).
\( \Leftrightarrow \left\{ \begin{array}{l}{x_D} - 2 = - 5\\{y_D} - 4 = 4\\{z_D} = - 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} = - 3\\{y_D} = 8\\{z_D} = - 7\end{array} \right.\). Vậy \(D\left( { - 3;8; - 7} \right)\).
Giả sử \(B'\left( {{x_{B'}};{y_{B'}};{z_{B'}}} \right)\). Ta có
\(\overrightarrow {BB'} = \left( {{x_{B'}} - 4;{y_{B'}};{z_{B'}}} \right)\).
\(\overrightarrow {DD'} = \left( {6 - \left( { - 3} \right);8 - 8;10 - \left( { - 7} \right)} \right) = \left( {9;0;17} \right)\).
\(ABCD\) là hình bình hành nên \(\overrightarrow {AD} = \overrightarrow {BC} \).
\( \Leftrightarrow \left\{ \begin{array}{l}{x_{B'}} - 4 = 9\\{y_{B'}} = 0\\{z_{B'}} = 17\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{B'}} = 13\\{y_{B'}} = 0\\{z_{B'}} = 17\end{array} \right.\). Vậy \(B'\left( {13;0;17} \right)\).
Bài 4 trang 76 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, quy tắc tính đạo hàm, và ứng dụng của đạo hàm để giải quyết các bài toán cụ thể. Việc nắm vững các khái niệm và kỹ năng này là rất quan trọng để đạt kết quả tốt trong các kỳ thi.
Bài 4 thường bao gồm các dạng bài tập sau:
Để giải bài 4 trang 76 một cách hiệu quả, bạn cần thực hiện theo các bước sau:
Ví dụ: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Giải:
f'(x) = 3x2 + 4x - 5
Đạo hàm là một khái niệm quan trọng trong Toán học, có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau như Vật lý, Kinh tế, và Kỹ thuật. Việc học tốt đạo hàm sẽ giúp bạn:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải bài 4 trang 76 sách bài tập Toán 12 Chân trời sáng tạo một cách hiệu quả. Hãy luyện tập thường xuyên và đừng ngần ngại tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè nếu bạn gặp khó khăn. Chúc bạn học tập tốt!