Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 10 trang 18 Sách bài tập Toán 12 - Chân trời sáng tạo. Bài viết này cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các bạn học sinh.
Cho hình thang cân có đáy nhỏ và hai cạnh bên bằng nhau và bằng 5. Tìm diện tích lớn nhất của hình thang cân đó.
Đề bài
Cho hình thang cân có đáy nhỏ và hai cạnh bên bằng nhau và bằng 5. Tìm diện tích lớn nhất của hình thang cân đó.
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính diện tích hình thang để tính diện tích \(S\left( x \right)\), sau đó tìm giá trị lớn nhất của hàm số \(S\left( x \right)\).
Lời giải chi tiết
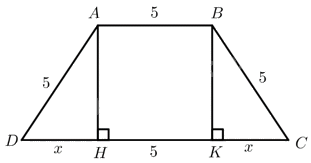
Xét hình thang cân \(ABCD\) có đáy nhỏ \(AB\), gọi \(H,K\) lần lượt là chân đường cao kẻ từ \(A\) và \(B\) xuống \(CD\).
Ta có:
\(C{\rm{D}} = 5 + 2{\rm{x}},AH = \sqrt {A{{\rm{D}}^2} - D{H^2}} = \sqrt {{5^2} - {x^2}} = \sqrt {25 - {x^2}} \)
Diện tích hình thang là:
\(S = \frac{1}{2}\left( {AB + C{\rm{D}}} \right).AH = \frac{1}{2}\left( {5 + 5 + 2{\rm{x}}} \right).\sqrt {25 - {x^2}} = \left( {5 + {\rm{x}}} \right).\sqrt {25 - {x^2}} \)
Do \(DH < AD\) nên \({\rm{x}} < 5\).
Xét hàm số \(S\left( x \right) = \left( {5 + {\rm{x}}} \right).\sqrt {25 - {x^2}} \) trên nửa khoảng \(\left[ {0;5} \right)\).
Ta có:
\(S'\left( x \right) = {\left( {5 + {\rm{x}}} \right)^\prime }.\sqrt {25 - {x^2}} + \left( {5 + {\rm{x}}} \right).{\left( {\sqrt {25 - {x^2}} } \right)^\prime } = \sqrt {25 - {x^2}} + \left( {5 + {\rm{x}}} \right).\frac{{ - {\rm{x}}}}{{\sqrt {25 - {x^2}} }} = \frac{{ - 2{{\rm{x}}^2} - 5x + 25}}{{\sqrt {25 - {x^2}} }}\)
\(S'\left( x \right) = 0 \Leftrightarrow x = \frac{5}{2}\) hoặc \(x = - 5\) (loại)
Bảng biến thiên của hàm số trên nửa khoảng \(\left[ {0;5} \right)\):
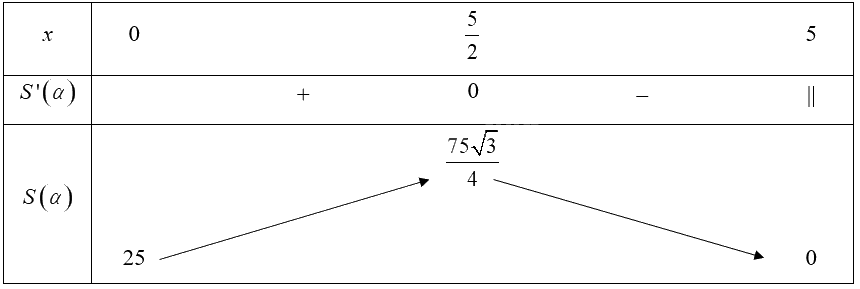
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{\left[ {0;5} \right)} S\left( x \right) = S\left( {\frac{5}{2}} \right) = \frac{{75\sqrt 3 }}{4}\).
Vậy hình thang cân \(ABCD\) có diện tích lớn nhất bằng \(\frac{{75\sqrt 3 }}{4}\).
Bài 10 trang 18 Sách bài tập Toán 12 - Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Bài 10 thường bao gồm các dạng bài tập sau:
Để giải quyết bài 10 trang 18 Sách bài tập Toán 12 - Chân trời sáng tạo một cách hiệu quả, học sinh cần nắm vững các phương pháp sau:
Ví dụ: Tìm cực trị của hàm số y = x3 - 3x2 + 2.
Giải:
Khi giải bài 10 trang 18 Sách bài tập Toán 12 - Chân trời sáng tạo, học sinh cần lưu ý những điều sau:
Học sinh có thể tham khảo thêm các tài liệu sau để học tập và rèn luyện:
Bài 10 trang 18 Sách bài tập Toán 12 - Chân trời sáng tạo là một bài tập quan trọng, giúp học sinh củng cố kiến thức về đạo hàm và rèn luyện kỹ năng giải toán. Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các bạn học sinh sẽ giải quyết bài tập này một cách dễ dàng và hiệu quả.