Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 4 trang 10 sách bài tập Toán 12 Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng theo dõi bài giải dưới đây để hiểu rõ hơn về cách giải bài tập này nhé!
Xét tính đơn điệu và tìm cực trị của các hàm số: a) (y = frac{{{x^2} + 8}}{{x + 1}}); b) (y = frac{{{x^2} - 8x + 10}}{{x - 2}}); c) (y = frac{{ - 2{x^2} + x + 2}}{{2x - 1}}); d) (y = frac{{ - {x^2} - 6x - 25}}{{x + 3}}).
Đề bài
Xét tính đơn điệu và tìm cực trị của các hàm số:
a) \(y = \frac{{{x^2} + 8}}{{x + 1}}\);
b) \(y = \frac{{{x^2} - 8x + 10}}{{x - 2}}\);
c) \(y = \frac{{ - 2{x^2} + x + 2}}{{2x - 1}}\);
d) \(y = \frac{{ - {x^2} - 6x - 25}}{{x + 3}}\).
Phương pháp giải - Xem chi tiết
Các bước để xét tính đơn điệu và tìm cực trị của hàm số \(f\left( x \right)\):
Bước 1. Tìm tập xác định \(D\) của hàm số.
Bước 2. Tính đạo hàm \(f'\left( x \right)\) của hàm số. Tìm các điểm \({x_1},{x_2},...,{x_n} \in D\) mà tại đó đạo hàm \(f'\left( x \right)\) bằng 0 hoặc không tồn tại.
Bước 3. Sắp xếp các điểm \({x_1},{x_2},...,{x_n}\) theo thứ tự tăng dần, xét dấu \(f'\left( x \right)\) và lập bảng biến thiên.
Bước 4. Nêu kết luận về các khoảng đồng biến, nghịch biến, cực trị của hàm số.
Lời giải chi tiết
a) Xét hàm số \(y = \frac{{{x^2} + 8}}{{x + 1}}\).
Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\).
Ta có \(y' = \frac{{{{\left( {{x^2} + 8} \right)}^\prime }\left( {x + 1} \right) - \left( {{x^2} + 8} \right){{\left( {x + 1} \right)}^\prime }}}{{{{\left( {x + 1} \right)}^2}}} \)
\(= \frac{{2{\rm{x}}\left( {x + 1} \right) - \left( {{x^2} + 8} \right)}}{{{{\left( {x + 1} \right)}^2}}} = \frac{{{x^2} + 2{\rm{x}} - 8}}{{{{\left( {x + 1} \right)}^2}}}\).
\(y' = 0 \Leftrightarrow x = 2\) hoặc \({\rm{x}} = - 4\).
Bảng biến thiên:
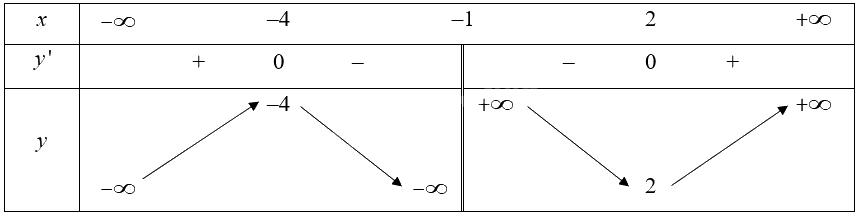
Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 4} \right)\) và \(\left( {2; + \infty } \right)\), nghịch biến trên các khoảng \(\left( { - 4; - 1} \right)\) và \(\left( { - 1;2} \right)\).
Hàm số đạt cực đại tại $x=-4,{{y}_{CĐ}}=-4$; hàm số đạt cực tiểu tại \(x = 2,{y_{CT}} = 2\).
b) Xét hàm số \(y = \frac{{{x^2} - 8x + 10}}{{x - 2}}\).
Tập xác định: \(D = \mathbb{R}\backslash \left\{ 2 \right\}\).
Ta có
\(\begin{array}{l}y' = \frac{{{{\left( {{x^2} - 8x + 10} \right)}^\prime }\left( {x - 2} \right) - \left( {{x^2} - 8x + 10} \right){{\left( {x - 2} \right)}^\prime }}}{{{{\left( {x - 2} \right)}^2}}} = \frac{{\left( {2{\rm{x}} - 8} \right)\left( {x - 2} \right) - \left( {{x^2} - 8x + 10} \right)}}{{{{\left( {x - 2} \right)}^2}}}\\ = \frac{{{x^2} - 4{\rm{x}} + 6}}{{{{\left( {x - 2} \right)}^2}}} = \frac{{{{\left( {x - 2} \right)}^2} + 2}}{{{{\left( {x - 2} \right)}^2}}} > 0\end{array}\)
Do đó hàm số đồng biến trên các khoảng \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\).
Hàm số không có cực trị.
c) Xét hàm số \(y = \frac{{ - 2{x^2} + x + 2}}{{2x - 1}}\).
Tập xác định: \(D = \mathbb{R}\backslash \left\{ {\frac{1}{2}} \right\}\).
Ta có
\(\begin{array}{l}y' = \frac{{{{\left( { - 2{x^2} + x + 2} \right)}^\prime }\left( {2x - 1} \right) - \left( { - 2{x^2} + x + 2} \right){{\left( {2x - 1} \right)}^\prime }}}{{{{\left( {2x - 1} \right)}^2}}} = \frac{{\left( { - 4{\rm{x}} + 1} \right)\left( {2x - 1} \right) - \left( { - 2{x^2} + x + 2} \right).2}}{{{{\left( {2x - 1} \right)}^2}}}\\ = \frac{{ - 4{x^2} + 4{\rm{x}} - 5}}{{{{\left( {2x - 1} \right)}^2}}} = \frac{{ - {{\left( {2x - 1} \right)}^2} - 4}}{{{{\left( {2x - 1} \right)}^2}}} < 0\end{array}\)
Do đó hàm số nghịch biến trên các khoảng \(\left( { - \infty ;\frac{1}{2}} \right)\) và \(\left( {\frac{1}{2}; + \infty } \right)\).
Hàm số không có cực trị.
d) Xét hàm số \(y = \frac{{ - {x^2} - 6x - 25}}{{x + 3}}\).
Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - 3} \right\}\).
Ta có
\(\begin{array}{l}y' = \frac{{{{\left( { - {x^2} - 6x - 25} \right)}^\prime }\left( {x + 3} \right) - \left( { - {x^2} - 6x - 25} \right){{\left( {x + 3} \right)}^\prime }}}{{{{\left( {x + 3} \right)}^2}}}\\ = \frac{{ - 2{\rm{x}}\left( {x + 3} \right) - \left( { - {x^2} - 6x - 25} \right)}}{{{{\left( {x + 3} \right)}^2}}} = \frac{{ - {{\rm{x}}^2} - 6{\rm{x}} + 7}}{{{{\left( {x + 3} \right)}^2}}}\end{array}\)
\(y' = 0 \Leftrightarrow x = 1\) hoặc \({\rm{x}} = - 7\).
Bảng biến thiên:
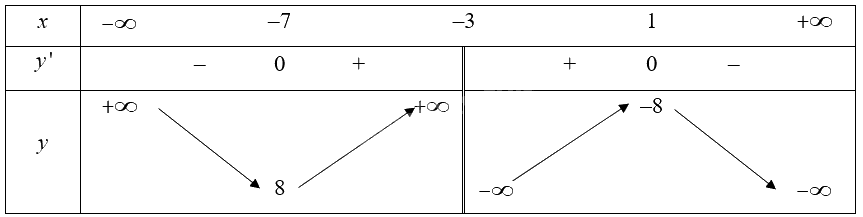
Hàm số đồng biến trên các khoảng \(\left( { - 7; - 3} \right)\) và \(\left( { - 3;1} \right)\), nghịch biến trên các khoảng \(\left( { - \infty ; - 7} \right)\) và \(\left( {1; + \infty } \right)\).
Hàm số đạt cực đại tại $x=1,{{y}_{CĐ}}=-8$; hàm số đạt cực tiểu tại \(x = - 7,{y_{CT}} = 8\).
Bài 4 trang 10 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào việc vận dụng các kiến thức về giới hạn của hàm số để giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững định nghĩa giới hạn, các tính chất của giới hạn và các phương pháp tính giới hạn thường gặp.
Bài 4 yêu cầu học sinh tính giới hạn của các hàm số khi x tiến tới một giá trị cụ thể. Các hàm số có thể là hàm đa thức, hàm hữu tỉ, hoặc các hàm số phức tạp hơn. Việc xác định đúng dạng hàm số và áp dụng phương pháp tính giới hạn phù hợp là rất quan trọng để có được kết quả chính xác.
Có nhiều phương pháp để tính giới hạn của hàm số, tùy thuộc vào dạng hàm số cụ thể. Một số phương pháp thường được sử dụng bao gồm:
Giả sử bài 4 yêu cầu tính giới hạn của hàm số f(x) = (x^2 - 1) / (x - 1) khi x tiến tới 1. Ta có thể giải bài tập này như sau:
Vậy, giới hạn của hàm số f(x) khi x tiến tới 1 là 2.
Để giải bài tập này một cách chính xác, học sinh cần lưu ý những điều sau:
Để hiểu rõ hơn về giới hạn của hàm số và các phương pháp tính giới hạn, học sinh có thể tham khảo thêm các tài liệu sau:
Bài 4 trang 10 sách bài tập Toán 12 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về giới hạn của hàm số. Bằng cách nắm vững các kiến thức lý thuyết và áp dụng các phương pháp giải phù hợp, học sinh có thể tự tin giải quyết bài tập này và các bài tập tương tự.
Giaitoan.edu.vn hy vọng bài giải chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về cách giải bài 4 trang 10 sách bài tập Toán 12 Chân trời sáng tạo. Chúc các em học tập tốt!