Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho bài tập 1 trang 13 SGK Toán 12 tập 1, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn Toán.
Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 11.
Đề bài
Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 11.
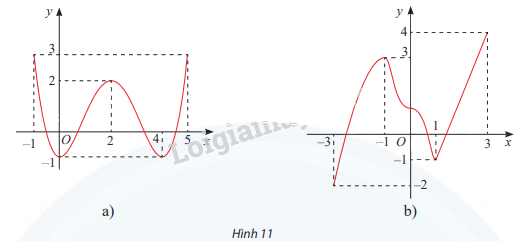
Phương pháp giải - Xem chi tiết
Quan sát đồ thị
Lời giải chi tiết
a) Hàm số đồng biến trên khoảng (0;2) và (4;5), nghịch biến trên khoảng (-1;0) và (2;4)
Hàm số đạt cực đại tại x = 2, \({y_{cd}} = f(2) = 2\), đạt cực tiểu tại x = 0, \({y_{ct}} = f(0) = - 1\) và x = 4, \({y_{ct}} = f(4) = - 1\)
b) Hàm số đồng biến trên khoảng (-3;-1) và (1;3), nghịch biến trên khoảng (-1;1)
Hàm số đạt cực đại tại x = -1, \({y_{cd}} = f( - 1) = 3\), đạt cực tiểu tại x = 1, \({y_{ct}} = f(1) = - 1\)
Bài tập 1 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo thuộc chương trình học về giới hạn của hàm số. Đây là một trong những khái niệm nền tảng quan trọng trong chương trình Toán học lớp 12, đóng vai trò then chốt trong việc hiểu và giải quyết các bài toán về đạo hàm, tích phân và các ứng dụng của chúng.
Bài tập 1 yêu cầu học sinh tính giới hạn của hàm số tại một điểm cho trước. Các hàm số thường gặp trong bài tập này bao gồm hàm đa thức, hàm hữu tỉ, và các hàm số đặc biệt khác. Để giải quyết bài tập này, học sinh cần nắm vững các định nghĩa và tính chất của giới hạn, cũng như các phương pháp tính giới hạn như phương pháp trực tiếp, phương pháp phân tích thành nhân tử, và phương pháp sử dụng định lý giới hạn.
Ví dụ 1: Tính limx→2 (x2 - 4) / (x - 2)
Giải:
Ta có: (x2 - 4) / (x - 2) = (x - 2)(x + 2) / (x - 2) = x + 2 (với x ≠ 2)
Vậy, limx→2 (x2 - 4) / (x - 2) = limx→2 (x + 2) = 2 + 2 = 4
Để củng cố kiến thức và kỹ năng giải bài tập giới hạn, các em có thể tự giải các bài tập sau:
Bài tập 1 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh làm quen với khái niệm giới hạn và rèn luyện kỹ năng giải toán. Hy vọng với những hướng dẫn và ví dụ minh họa trên, các em sẽ tự tin hơn trong việc giải quyết bài tập này và các bài tập tương tự trong tương lai.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!