Chào mừng bạn đến với bài học lý thuyết Phương trình đường thẳng trong không gian chương trình Toán 12 Chân trời sáng tạo tại giaitoan.edu.vn. Bài viết này sẽ cung cấp kiến thức nền tảng, công thức và các ví dụ minh họa giúp bạn hiểu rõ về chủ đề này.
Chúng tôi cam kết mang đến cho bạn trải nghiệm học tập trực tuyến hiệu quả và thú vị. Hãy cùng bắt đầu khám phá thế giới hình học không gian!
1. Phương trình đường thẳng trong không gian Vecto chỉ phương của đường thẳng
1. Phương trình đường thẳng trong không gian
Vecto chỉ phương của đường thẳng
| Vecto \(\overrightarrow a \ne \overrightarrow 0 \) được gọi là vecto chỉ phương của đường thẳng \(d\) nếu giá của \(\overrightarrow a \) song song hoặc trùng với \(d\). |
Nếu \(\overrightarrow a \) là vecto chỉ phương của \(d\) thì \(k\overrightarrow a \) \((k \ne 0)\) cũng là vecto chỉ phương của d.
Ví dụ: Trong không gian Oxyz, cho hình chóp O.ABC có A(2;0;0), B(0;4;0) và C(0;0;7).
a) Tìm tọa độ một vecto chỉ phương của mỗi đường thẳng AB, AC.
b) Vecto \(\overrightarrow v = ( - 1;2;0)\) có là vecto chỉ phương của đường thẳng AB không?
Giải:
a) Ta có \(\overrightarrow {AB} = ( - 2;4;0)\) là một vecto chỉ phương của đường thẳng AB.
\(\overrightarrow {AC} = ( - 2;0;7)\) là một vecto chỉ phương của đường thẳng AC.
b) Vì \(\overrightarrow v = ( - 1;2;0) = \frac{1}{2}\overrightarrow {AB} \) nên \(\overrightarrow v \) là một vecto chỉ phương của đường thẳng AB.
Phương trình tham số của đường thẳng
Trong không gian Oxyz, cho đường thẳng \(\Delta \) đi qua điểm \({M_0}({x_0};{y_0};{z_0})\) và có vecto chỉ phương \(\overrightarrow u = (a;b;c)\). Hệ phương trình: \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\) được gọi là phương trình tham số của đường thẳng \(\Delta \) (t là tham số, \(t \in R\)). |
Mỗi giá trị của tham số t xác định duy nhất một điểm A trên \(\Delta \) và ngược lại.
Ví dụ: Cho đường thẳng d có phương trình tham số \(\left\{ {\begin{array}{*{20}{c}}{x = - 2 + 6t}\\{y = 11 + 2t}\\{z = 4t}\end{array}} \right.\) \((t \in \mathbb{R})\).
a) Tìm hai vecto chỉ phương của d.
b) Tìm các điểm trên d ứng với t lần lượt bằng 0; 2; -3.
Giải:
a) Từ phương trình tham số, ta có \(\overrightarrow a = (6;2;4)\) là một vecto chỉ phương của d.
Chọn \(\overrightarrow b = \frac{1}{2}\overrightarrow a = (3;1;2)\), ta có \(\overrightarrow b \) cũng là một vecto chỉ phương của d.
b) Thay t = 0 vào phương trình tham số của d ta được
\(\left\{ {\begin{array}{*{20}{c}}{x = - 2 + 6.0}\\{y = 11 + 2.0}\\{z = 4.0}\end{array}} \right.\) hay \(\left\{ {\begin{array}{*{20}{c}}{x = - 2}\\{y = 11}\\{z = 0}\end{array}} \right.\)
Vậy A(-2;11;0).
Tương tự, với t = 2 thì B(10;15;8), với t = 3 thì C(-20;5;-12).
Phương trình chính tắc của đường thẳng
Trong không gian Oxyz, cho đường thẳng \(\Delta \) đi qua điểm \(A({x_0};{y_0};{z_0})\) và có vecto chỉ phương \(\overrightarrow u = (a;b;c)\) với a, b, c là các số khác 0. Hệ phương trình \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b} = \frac{{z - {z_0}}}{c}\) được gọi là phương trình chính tắc của đường thẳng \(\Delta \). |
Ví dụ: Viết phương trình chính tắc của đường thẳng d đi qua điểm \({M_0}(1;2;3)\) và nhận \(\overrightarrow a = (4;5; - 7)\) làm vecto chỉ phương.
Giải: Đường thẳng d có phương trình chính tắc là \(\frac{{x - 1}}{4} = \frac{{y - 2}}{5} = \frac{{z - 3}}{{ - 7}}\).
Phương trình chính tắc và phương trình tham số của đường thẳng đi qua hai điểm
Trong không gian Oxyz, cho hai điểm phân biệt \({A_1}({x_1};{y_1};{z_1})\) và \({A_2}({x_2};{y_2};{z_2})\). Đường thẳng \({A_1}{A_2}\) có vecto chỉ phương \(\overrightarrow {{A_1}{A_2}} = ({x_2} - {x_1};{y_2} - {y_1};{z_2} - {z_1})\) - Đường thẳng \({A_1}{A_2}\) có phương trình tham số là \(\left\{ \begin{array}{l}x = {x_1} + ({x_2} - {x_1})t\\y = {y_1} + ({y_2} - {y_1})t\\z = {z_1} + ({z_2} - {z_1})t\end{array} \right.\) \((t \in R)\). - Trong trường hợp \({x_1} \ne {x_2},{y_1} \ne {y_2},{z_1} \ne {z_2}\) thì đường thẳng \({A_1}{A_2}\) có phương trình chính tắc là: \(\frac{{x - {x_1}}}{{{x_2} - {x_1}}} = \frac{{y - {y_1}}}{{{y_2} - {y_1}}} = \frac{{z - {z_1}}}{{{z_2} - {z_1}}}\). |
Ví dụ: Viết phương trình tham số và phương trình chính tắc của đường thẳng AB, biết A(1;1;5) và B(3;5;8).
Giải: Đường thẳng AB có vecto chỉ phương là \(\overrightarrow {AB} = (2;4;3)\) nên có phương trình tham số \(\left\{ {\begin{array}{*{20}{c}}{x = 1 + 2t}\\{y = 1 + 4t}\\{z = 5 + 3t}\end{array}} \right.\) và phương trình chính tắc \(\frac{{x - 1}}{2} = \frac{{y - 1}}{4} = \frac{{z - 5}}{3}\).
2. Vị trí tương đối giữa hai đường thẳng. Điều kiện để hai đường thẳng vuông góc
Điều kiện để hai đường thẳng song song hoặc trùng nhau
Trong không gian Oxyz, cho hai đường thẳng \(d,d'\) có vecto chỉ phương tương ứng là \(\overrightarrow a ({x_1};{y_1};{z_1})\), \(\overrightarrow {a'} ({x_2};{y_2};{z_2})\). Gọi \(M({x_0};{y_0};{z_0}) \in d\). Khi đó + \(d//d' \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow a = k\overrightarrow {a'} ,k \in \mathbb{R}\\M \notin d'\end{array} \right.\) + \(d \equiv d' \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow a = k\overrightarrow {a'} ,k \in \mathbb{R}\\M \in d'\end{array} \right.\) |
Ví dụ: Kiểm tra tính song song hoặc trùng nhau của các cặp đường thẳng sau:
a) d: \(\left\{ {\begin{array}{*{20}{c}}{x = 1 + t}\\{y = 2 + t}\\{z = 1 + 2t}\end{array}} \right.\) và d’: \(\left\{ {\begin{array}{*{20}{c}}{x = 2 + 2t'}\\{y = 5 + 2t'}\\{z = 1 + 4t'}\end{array}} \right.\)
b) d: \(\frac{{x - 1}}{1} = \frac{{y - 2}}{1} = \frac{{z - 1}}{2}\) và d: \(\frac{{x - 2}}{3} = \frac{{y - 3}}{3} = \frac{{z - 3}}{6}\)
Giải:
a) Đường thẳng d đi qua điểm M(1;2;1) và có vecto chỉ phương \(\overrightarrow a = (2;2;4) = 2\overrightarrow a \).
Thay tọa độ điểm M vào phương trình của d’, ta được
\(\left\{ {\begin{array}{*{20}{c}}{1 = 2 + 2t'}\\{2 = 5 + 2t'}\\{5 = 1 + 4t'}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{t' = - \frac{1}{2}}\\{t' = - \frac{3}{2}}\\{t' = 0}\end{array}} \right.\) (vô nghiệm).
Suy ra M không thuộc d’. Vậy d//d’.
b) Đường thẳng d đi qua điểm M(1;2;1) và có vecto chỉ phương \(\overrightarrow a = (2;2;4) = 2\overrightarrow a \).
Đường thẳng d’ có vecto chỉ phương \(\overrightarrow a = (3;3;6) = 3\overrightarrow a \).
Thay tọa độ điểm M vào phương trình của d’, ta được
\(\frac{{1 - 2}}{3} = \frac{{2 - 3}}{3} = \frac{{1 - 3}}{6}\).
Phương trình nghiệm đúng, suy ra M thuộc d’. Vậy d\( \equiv \)d’.
Điều kiện để hai đường thẳng cắt nhau hoặc chéo nhau
Trong không gian Oxyz, cho hai đường thẳng \(d,d'\) có vecto chỉ phương tương ứng là \(\overrightarrow a ({x_1};{y_1};{z_1})\), \(\overrightarrow {a'} ({x_2};{y_2};{z_2})\). Gọi \(M({x_0};{y_0};{z_0}) \in d\), \(M'({x_0}';{y_0}';{z_0}') \in d'\). Khi đó + \(d,d'\) cắt nhau \( \Leftrightarrow \left[ {\overrightarrow a ,\overrightarrow {a'} } \right].\overrightarrow {MM'} = 0\). + \(d,d'\) chéo nhau \( \Leftrightarrow \left[ {\overrightarrow a ,\overrightarrow {a'} } \right].\overrightarrow {MM'} \ne 0\). |
Ví dụ: Xét vị trí tương đối giữa hai đường thẳng d và d’ trong mỗi trường hợp sau:
a) d: \(\left\{ {\begin{array}{*{20}{c}}{x = t}\\{y = 1 + t}\\{z = 2 + t}\end{array}} \right.\) và d’: \(\left\{ {\begin{array}{*{20}{c}}{x = 1 + 2t'}\\{y = 2 + 5t'}\\{z = 3 + t'}\end{array}} \right.\)
b) d: \(\left\{ {\begin{array}{*{20}{c}}{x = 1 + t}\\{y = 2 + t}\\{z = 3 + t}\end{array}} \right.\) và d’ \(\frac{{x - 1}}{2} = \frac{{y - 2}}{5} = \frac{{z - 9}}{6}\)
Giải:
a) d và d’ có vecto chỉ phương lần lượt là \(\overrightarrow a = (1;1;1)\) và \(\overrightarrow {a'} = (2;5;1)\).
Ta có \(\frac{1}{2} \ne \frac{1}{5}\), suy ra \(\overrightarrow a \) và \(\overrightarrow {a'} \) không cùng phương. Vậy d và d’ hoặc cắt nhau hoặc chéo nhau.
Xét hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{t = 1 + 2t'}\\{t + 1 = 2 + 5t'}\\{t + 2 = 3 + t'}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{t - 2t' = 1}\\{t - 5t' = 1}\\{t - t' = 1}\end{array}} \right.\)
Giải hệ phương trình được t = 1, t’ = 0.
Vậy d cắt d’ tại điểm M(1;2;3).
b) d và d’ có vecto chỉ phương lần lượt là \(\overrightarrow a = (1;1;1)\) và \(\overrightarrow {a'} = (2;5;6)\).
Ta có \(\frac{1}{2} \ne \frac{1}{5}\), suy ra \(\overrightarrow a \) và \(\overrightarrow {a'} \) không cùng phương. Vậy d và d’ hoặc cắt nhau hoặc chéo nhau.
d’ có phương trình tham số là \(\left\{ {\begin{array}{*{20}{c}}{x = 1 + 2t'}\\{y = 2 + 5t'}\\{z = 9 + 6t'}\end{array}} \right.\)
Xét hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{1 + t = 1 + 2t'}\\{2 + t = 2 + 5t'}\\{3 + t = 9 + 6t'}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{t - 2t' = 0}\\{t - 5t' = 0}\\{t - 6t' = 6}\end{array}} \right.\)
Giải hệ trên không tìm được t, t’ thỏa mãn.
Vậy d và d’ chéo nhau.
Điều kiện để hai đường thẳng vuông góc
Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) tương ứng có vecto chỉ phương \(\overrightarrow {{u_1}} ({a_1};{b_1};{c_1})\), \(\overrightarrow {{u_2}} ({a_2};{b_2};{c_2})\). Khi đó: \({\Delta _1} \bot {\Delta _2} \Leftrightarrow \overrightarrow {{u_1}} \cdot \overrightarrow {{u_2}} = 0 \Leftrightarrow {a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2} = 0\) |
Ví dụ: Kiểm tra tính vuông góc của các cặp đường thẳng sau:
a) d: \(\frac{{x - 2}}{3} = \frac{{y - 1}}{5} = \frac{{z - 3}}{1}\) và d’: \(\left\{ {\begin{array}{*{20}{c}}{x = - 2 + t}\\{y = 7 + t}\\{z = 9 - 8t}\end{array}} \right.\)
b) d: \(\frac{{x - 2}}{3} = \frac{{y - 1}}{5} = \frac{{z - 3}}{1}\) và d’ \(\frac{{x + 2}}{2} = \frac{{y - 7}}{1} = \frac{{z - 9}}{1}\)
Giải:
a) d và d’ có vecto chỉ phương lần lượt là \(\overrightarrow a = (3;5;1)\) và \(\overrightarrow {a'} = (1;1; - 8)\).
Ta có \(\overrightarrow a .\overrightarrow {a'} = 3 + 5 - 8 = 0\). Vậy d và d’ vuông góc với nhau.
b) d và d’ có vecto chỉ phương lần lượt là \(\overrightarrow a = (3;5;1)\) và \(\overrightarrow {a'} = (2;1;1)\).
Ta có \(\overrightarrow a .\overrightarrow {a'} = 6 + 5 + 1 \ne 0\). Vậy và d’ không vuông góc với nhau.
3. Góc
Góc giữa hai đường thẳng
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) có vecto chỉ phương lần lượt là \(\overrightarrow {{u_1}} ({a_1};{b_1};{c_1})\), \(\overrightarrow {{u_2}} ({a_2};{b_2};{c_2})\). Khi đó, ta có: \(\cos ({\Delta _1},{\Delta _2}) = \left| {\cos (\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} )} \right| = \frac{{\left| {\overrightarrow {{u_1}} .\overrightarrow {{u_2}} } \right|}}{{\left| {\overrightarrow {{u_1}} } \right|.\left| {\overrightarrow {{u_2}} } \right|}} = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}} \right|}}{{\sqrt {a_1^2 + b_1^2 + c_1^2} .\sqrt {a_2^2 + b_2^2 + c_2^2} }}\) |
Ví dụ: Tính góc giữa hai đường thẳng
d: \(\frac{{x + 2}}{1} = \frac{{y + 4}}{2} = \frac{{z + 1}}{2}\) và d’: \(\left\{ {\begin{array}{*{20}{c}}{x = 2 - 2t}\\{y = 2 - 2t}\\{z = 1 + t}\end{array}} \right.\).
Giải: d và d’ có vecto chỉ phương lần lượt là \(\overrightarrow a = (1;2;2)\) và \(\overrightarrow {a'} = ( - 2; - 2;1)\).
Ta có \(\cos (d,d') = \frac{{\left| {1.1 + 2.1 + 1.2} \right|}}{{\sqrt {{1^2} + {2^2} + {1^2}} .\sqrt {{1^2} + {1^2} + {2^2}} }} = \frac{4}{9}\).
Suy ra \((d,d') \approx {63^o}36'\).
Góc giữa đường thẳng và mặt phẳng
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \(\Delta \) có vecto chỉ phương lần lượt là \(\overrightarrow u ({a_1};{b_1};{c_1})\) và mặt phẳng (P) có vecto pháp tuyến \(\overrightarrow n ({a_2};{b_2};{c_2})\). Gọi \((\Delta ,(P))\) là góc giữa đường thẳng \(\Delta \) và mặt phẳng (P). Khi đó, ta có: \(\sin (\Delta ,(P)) = \left| {\cos (\overrightarrow u ,\overrightarrow n )} \right| = \frac{{\left| {\overrightarrow u .\overrightarrow n } \right|}}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow n } \right|}} = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}} \right|}}{{\sqrt {a_1^2 + b_1^2 + c_1^2} .\sqrt {a_2^2 + b_2^2 + c_2^2} }}\) |
Nếu đường thẳng có vecto chỉ phương cùng phương với vecto pháp tuyến của mặt phẳng thì đường thẳng vuông góc với mặt phẳng.
Ví dụ: Tính góc giữa đường thẳng d: \(\frac{{x + 2}}{2} = \frac{{y + 4}}{2} = \frac{{z + 1}}{1}\) và mặt phẳng (P): \(x + z + 24 = 0\).
Giải: Đường thẳng d có vecto chỉ phương \(\overrightarrow a = (2;2;1)\). Mặt phẳng (P) có vecto pháp tuyến \(\overrightarrow n = (1;0;1)\).
Ta có \(\sin (d,(P)) = \frac{{\left| {2.1 + 2.0 + 1.1} \right|}}{{\sqrt {{2^2} + {2^2} + {1^2}} .\sqrt {{1^2} + {0^2} + {1^2}} }} = \frac{1}{{\sqrt 2 }}\).
Suy ra \((d,(P)) = {45^o}\).
Góc giữa hai mặt phẳng
Góc giữa hai mặt phẳng \(({P_1}),({P_2})\) là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó, kí hiệu là \(\left( {({P_1}),({P_2})} \right)\).
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng \(({P_1}),({P_2})\) có vecto pháp tuyến lần lượt là \(\overrightarrow {{n_1}} ({A_1};{B_1};{C_1})\), \(\overrightarrow {{n_2}} ({A_2};{B_2};{C_2})\). Khi đó, ta có: \(\cos \left( {({P_1}),({P_2})} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {{A_1}{A_2} + {B_1}{B_2} + {C_1}{C_2}} \right|}}{{\sqrt {A_1^2 + B_1^2 + C_1^2} .\sqrt {A_2^2 + B_2^2 + C_2^2} }}\) |
Nếu hai mặt phẳng có hai vecto pháp tuyến vuông góc với nhau thì hai mặt phẳng vuông góc với nhau.
Ví dụ: Tính góc giữa hai mặt phẳng (P): \(x + y - 2z + 9 = 0\) và (P’): \(3x - 5y + z + 2024 = 0\).
Giải: (P) và (P’) có vecto pháp tuyến lần lượt là \(\overrightarrow n = (1;1; - 2)\), \(\overrightarrow {n'} = (3; - 5;1)\).
Ta có \(\cos \left( {(P),(P')} \right) = \frac{{\left| {1.3 + 1.( - 5) + ( - 2).1} \right|}}{{\sqrt {{1^2} + {1^2} + {{( - 2)}^2}} .\sqrt {{3^2} + {{( - 5)}^2} + {1^2}} }} = \frac{4}{{\sqrt {210} }}\).
Suy ra \(\left( {(P),(P')} \right) \approx {73^o}59'\).
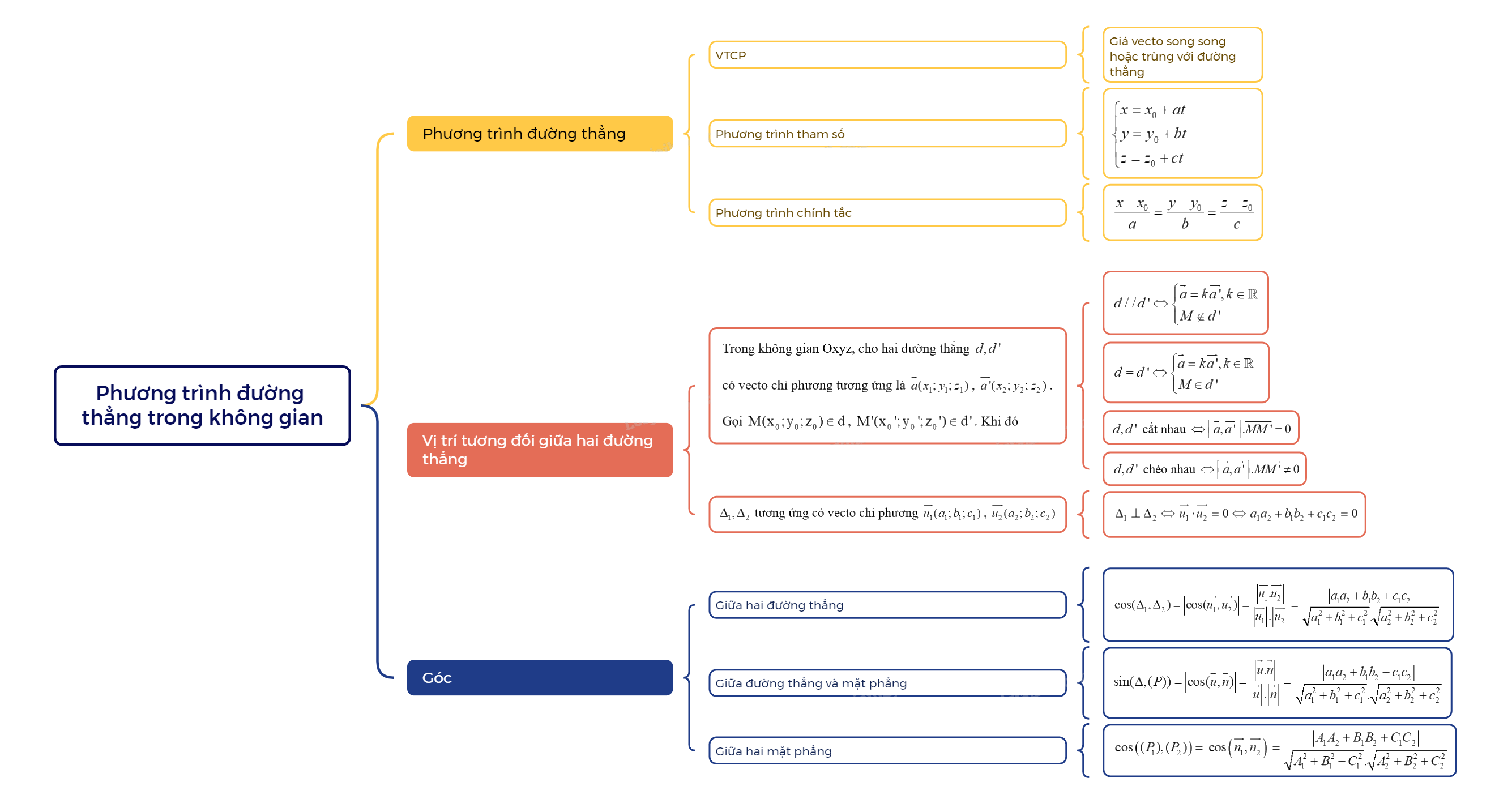
Trong chương trình Toán 12 Chân trời sáng tạo, kiến thức về phương trình đường thẳng trong không gian đóng vai trò quan trọng, là nền tảng cho việc giải quyết các bài toán về quan hệ tương giao giữa đường thẳng và mặt phẳng, đường thẳng và đường thẳng trong không gian. Bài viết này sẽ trình bày chi tiết lý thuyết, các dạng phương trình và phương pháp áp dụng để giải quyết các bài toán liên quan.
Một đường thẳng Δ trong không gian được xác định bởi một điểm A(x0, y0, z0) và một vectơ chỉ phương u = (a, b, c). Vectơ chỉ phương u có hướng chỉ ra hướng của đường thẳng Δ.
Có ba dạng phương trình chính để biểu diễn một đường thẳng trong không gian:
{ x = x0 + at; y = y0 + bt; z = z0 + ct; }
(x - x0)/a = (y - y0)/b = (z - z0)/c
x/a + y/b + z/c = 1
Cho đường thẳng Δ có vectơ chỉ phương u và vectơ v.
Cho hai đường thẳng Δ1 và Δ2 có vectơ chỉ phương lần lượt là u1 và u2, và một điểm A thuộc Δ1.
Khoảng cách d từ điểm M(xM, yM, zM) đến đường thẳng Δ có phương trình tham số { x = x0 + at; y = y0 + bt; z = z0 + ct; } được tính theo công thức:
d = |[AM x u]| / |u|
Trong đó AM = (xM - x0, yM - y0, zM - z0).
Ví dụ 1: Lập phương trình đường thẳng đi qua điểm A(1, 2, 3) và có vectơ chỉ phương u = (4, -5, 6).
Giải: Phương trình tham số của đường thẳng là: { x = 1 + 4t; y = 2 - 5t; z = 3 + 6t; }
Ví dụ 2: Xác định vị trí tương đối giữa hai đường thẳng Δ1: { x = 1 + t; y = 2 + 2t; z = 3 + 3t; } và Δ2: { x = 2 + 2t; y = 3 + 4t; z = 4 + 6t; }
Giải: Vectơ chỉ phương của Δ1 là u1 = (1, 2, 3) và của Δ2 là u2 = (2, 4, 6). Ta thấy u2 = 2u1, do đó hai đường thẳng song song. Điểm A(1, 2, 3) thuộc Δ1, thay vào phương trình của Δ2 ta thấy A không thuộc Δ2. Vậy hai đường thẳng song song.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết phương trình đường thẳng trong không gian Toán 12 Chân trời sáng tạo. Chúc bạn học tập tốt!