Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 19,20 SGK Toán 12 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán.
Bài tập này thuộc chương trình học Toán 12 tập 1, tập trung vào các kiến thức cơ bản về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế.
Đường tiệm cận đứng
Trả lời câu hỏi Thực hành 1 trang 20 SGK Toán 12 Chân trời sáng tạo
Tìm tiệm cận đứng của đồ thị các hàm số sau:
a) \(f(x) = \frac{{2x + 3}}{{ - x + 5}}\)
b) \(g(x) = \frac{{{x^2} - 2x}}{{x - 1}}\)
Phương pháp giải:
Đường thẳng x = a được gọi là một đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau thoả mãn:\(\mathop {\lim f(x) = }\limits_{x \to {a^ - }} + \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ + }} + \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ - }} - \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ + }} - \infty \)
Lời giải chi tiết:
a) Xét \(f(x) = \frac{{2x + 3}}{{ - x + 5}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 5\} \)
Ta có: \(\mathop {\lim f(x) = }\limits_{x \to {5^ - }} \mathop {\lim }\limits_{x \to {5^ - }} \frac{{2x + 3}}{{ - x + 5}} = + \infty \), \(\mathop {\lim f(x) = }\limits_{x \to {5^ + }} \mathop {\lim }\limits_{x \to {5^ + }} \frac{{2x + 3}}{{ - x + 5}} = - \infty \)
Vậy đường thẳng x = 5 là một tiệm cận đứng của đồ thị hàm số
b) Xét \(g(x) = \frac{{{x^2} - 2x}}{{x - 1}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 1\} \)
Ta có: \(\mathop {\lim g(x) = }\limits_{x \to {1^ - }} \mathop {\lim }\limits_{x \to {1^ - }} \frac{{{x^2} - 2x}}{{x - 1}} = + \infty \), \(\mathop {\lim g(x) = }\limits_{x \to {1^ + }} \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} - 2x}}{{x - 1}} = - \infty \)
Vậy đường thẳng x = 1 là một tiệm cận đứng của đồ thị hàm số
Trả lời câu hỏi Khám phá 1 trang 19 SGK Toán 12 Chân trời sáng tạo
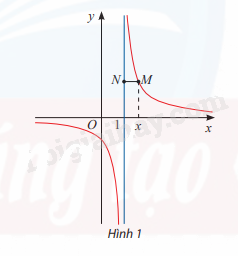
Cho hàm số \(y = \frac{1}{{x - 1}}\)có đồ thị như Hình 1.
a) Tìm \(\mathop {\lim }\limits_{x \to {1^ + }} = \frac{1}{{x - 1}},\mathop {\lim }\limits_{x \to {1^ - }} = \frac{1}{{x - 1}}\)
b) Gọi M là điểm trên đồ thị có hoành độ x. Đường thẳng đi qua M và vuông góc với trục Oy cắt đường thẳng x = 1 tại điểm N. Tính MN theo x và nhận xét về MN khi \(x \to {1^ + }\) và \(x \to {1^ - }\)
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
a) Từ đồ thị ta thấy:
Khi x tiến dần tới 1 về bên phải thì y tiến dần đến \( + \infty \), vậy \(\mathop {\lim }\limits_{x \to {1^ + }} = \frac{1}{{x - 1}} = + \infty \)
Khi x tiến dần tới 1 về bên trái thì y tiến dần đến \( - \infty \), vậy \(\mathop {\lim }\limits_{x \to {1^ - }} = \frac{1}{{x - 1}} = - \infty \)
b) MN = x – 1
Khi \(x \to {1^ + }\) thì MN tiến dần về \( + \infty \) và khi \(x \to {1^ - }\) thì MN tiến dần về \( - \infty \)
Trả lời câu hỏi Khám phá 1 trang 19 SGK Toán 12 Chân trời sáng tạo
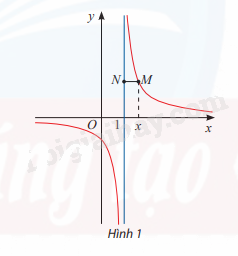
Cho hàm số \(y = \frac{1}{{x - 1}}\)có đồ thị như Hình 1.
a) Tìm \(\mathop {\lim }\limits_{x \to {1^ + }} = \frac{1}{{x - 1}},\mathop {\lim }\limits_{x \to {1^ - }} = \frac{1}{{x - 1}}\)
b) Gọi M là điểm trên đồ thị có hoành độ x. Đường thẳng đi qua M và vuông góc với trục Oy cắt đường thẳng x = 1 tại điểm N. Tính MN theo x và nhận xét về MN khi \(x \to {1^ + }\) và \(x \to {1^ - }\)
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
a) Từ đồ thị ta thấy:
Khi x tiến dần tới 1 về bên phải thì y tiến dần đến \( + \infty \), vậy \(\mathop {\lim }\limits_{x \to {1^ + }} = \frac{1}{{x - 1}} = + \infty \)
Khi x tiến dần tới 1 về bên trái thì y tiến dần đến \( - \infty \), vậy \(\mathop {\lim }\limits_{x \to {1^ - }} = \frac{1}{{x - 1}} = - \infty \)
b) MN = x – 1
Khi \(x \to {1^ + }\) thì MN tiến dần về \( + \infty \) và khi \(x \to {1^ - }\) thì MN tiến dần về \( - \infty \)
Trả lời câu hỏi Thực hành 1 trang 20 SGK Toán 12 Chân trời sáng tạo
Tìm tiệm cận đứng của đồ thị các hàm số sau:
a) \(f(x) = \frac{{2x + 3}}{{ - x + 5}}\)
b) \(g(x) = \frac{{{x^2} - 2x}}{{x - 1}}\)
Phương pháp giải:
Đường thẳng x = a được gọi là một đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau thoả mãn:\(\mathop {\lim f(x) = }\limits_{x \to {a^ - }} + \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ + }} + \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ - }} - \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ + }} - \infty \)
Lời giải chi tiết:
a) Xét \(f(x) = \frac{{2x + 3}}{{ - x + 5}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 5\} \)
Ta có: \(\mathop {\lim f(x) = }\limits_{x \to {5^ - }} \mathop {\lim }\limits_{x \to {5^ - }} \frac{{2x + 3}}{{ - x + 5}} = + \infty \), \(\mathop {\lim f(x) = }\limits_{x \to {5^ + }} \mathop {\lim }\limits_{x \to {5^ + }} \frac{{2x + 3}}{{ - x + 5}} = - \infty \)
Vậy đường thẳng x = 5 là một tiệm cận đứng của đồ thị hàm số
b) Xét \(g(x) = \frac{{{x^2} - 2x}}{{x - 1}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 1\} \)
Ta có: \(\mathop {\lim g(x) = }\limits_{x \to {1^ - }} \mathop {\lim }\limits_{x \to {1^ - }} \frac{{{x^2} - 2x}}{{x - 1}} = + \infty \), \(\mathop {\lim g(x) = }\limits_{x \to {1^ + }} \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} - 2x}}{{x - 1}} = - \infty \)
Vậy đường thẳng x = 1 là một tiệm cận đứng của đồ thị hàm số
Mục 1 của SGK Toán 12 tập 1 chương trình Chân trời sáng tạo tập trung vào việc ôn tập và mở rộng kiến thức về đạo hàm. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các công thức đạo hàm cơ bản, quy tắc tính đạo hàm của hàm hợp, đạo hàm của hàm lượng giác, hàm mũ, hàm logarit và ứng dụng đạo hàm để giải quyết các bài toán liên quan đến cực trị, đơn điệu của hàm số.
Để giải bài tập này, học sinh cần nắm vững các công thức đạo hàm cơ bản và quy tắc tính đạo hàm. Ví dụ, để tính đạo hàm của hàm số y = x2 + 3x - 2, ta sử dụng công thức đạo hàm của hàm đa thức: y' = 2x + 3.
Để giải bài tập này, học sinh cần sử dụng quy tắc tính đạo hàm của hàm hợp. Ta có y' = cos(2x) * 2 = 2cos(2x).
Để giải bài tập này, học sinh cần tìm các điểm dừng của hàm số bằng cách giải phương trình y' = 0. Sau đó, ta xét dấu đạo hàm bậc hai để xác định xem các điểm dừng là điểm cực đại hay điểm cực tiểu.
Đạo hàm có rất nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng rằng với lời giải chi tiết và phương pháp giải hiệu quả mà giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc giải quyết các bài tập về đạo hàm và ứng dụng của đạo hàm. Chúc các em học tập tốt!