Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 1 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 12 tập 1, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em học sinh nắm vững kiến thức, tự tin giải quyết các bài toán và đạt kết quả cao trong môn Toán.
Cực trị của hàm số
Trả lời câu hỏi Thực hành 4 trang 11 SGK Toán 12 Chân trời sáng tạo
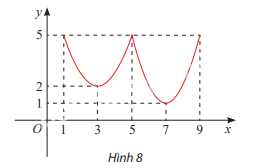
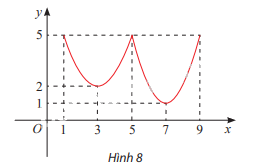
Tìm các điểm cực trị của hàm số y = f(x) có đồ thị cho ở Hình 8
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
Hàm số y = f (x) có:
x = 5 là điểm cực đại vì f (x) < f(5) với mọi \(x \in \left( {3;{\rm{ 7}}} \right)\backslash \left\{ 5 \right\}\), \({y_{cd}} = f(5) = 5\)
x = 3 là điểm cực tiểu vì f(x) > f(3) với mọi \(x \in \left( {1;{\rm{ 5}}} \right)\backslash \left\{ 3 \right\}\), \({y_{ct}} = f(3) = 2\)
x=7 là điểm cực tiểu vì f(x) > f(7) với mọi \(x \in \left( {5;{\rm{ 9}}} \right)\backslash \left\{ 7 \right\}\), \({y_{ct}} = f(7) = 1\)
Trả lời câu hỏi Khám phá 2 trang 10 SGK Toán 12 Chân trời sáng tạo
Quan sát đồ thị của hàm số \(y = f\left( x \right) = {x^3}--3{x^2} + 1{\rm{ }}\) trong Hình 5.
a) Tìm khoảng (a; b) chứa điểm x = 0 mà trên đó f(x) < f(0) với mọi \(x \ne 0\).
b) Tìm khoảng (a; b) chứa điểm x = 2 mà trên đó f(x) > f(2) với mọi \(x \ne 2\).
c) Tồn tại hay không khoảng (a; b) chứa điểm x = 1 mà trên đó f(x) > f(1) với mọi \(x \ne 1\) hoặc f(x) < f(1) với mọi \(x \ne 1\)?
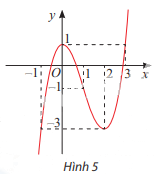
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
a) Trên khoảng (-1; 2), f(x) < f(0) với mọi \(x \ne 0\)
b) Trên khoảng (0; 3), f(x) > f(2) với mọi \(x \ne 2\)
c) Không tồn tại khoảng (a; b) chứa điểm x = 1 mà trên đó f(x) > f(1) với mọi \(x \ne 1\) hoặc f(x) < f(1) với mọi \(x \ne 1\)
Trả lời câu hỏi Thực hành 5 trang 12 SGK Toán 12 Chân trời sáng tạo
Tìm cực trị của hàm số \(g\left( x \right) = \frac{{{x^2} + x + 4}}{{x + 1}}\)
Phương pháp giải:
Tìm tập xác định, g’(x) và lập bảng biến thiên
Lời giải chi tiết:
Tập xác định: \(D = \mathbb{R}\backslash \{ - 1\} \)
\(g'(x) = \frac{{{x^2} + 2x - 3}}{{{x^2} + 2x + 1}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 3\end{array} \right.\)
Bảng biến thiên:
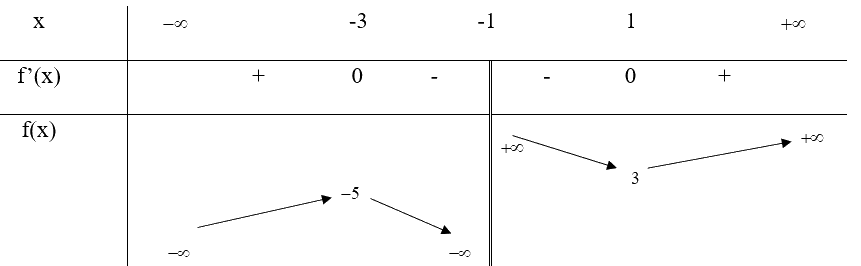
Vậy hàm số đạt cực tiểu tại x = -3, \({y_{ct}} = f( - 3) = - 5\), đạt cực đại tại x = 1, \({y_{cd}} = f(1) = 3\)
Trả lời câu hỏi Vận dụng 2 trang 12 SGK Toán 12 Chân trời sáng tạo
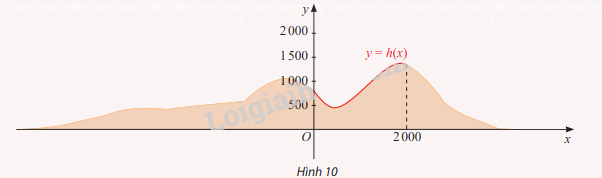
Một phần lát cắt của dãy núi có độ cao tính bằng mét được mô tả bởi hàm số \(y = h\left( x \right) = - \frac{1}{{1320000}}{x^3} + \frac{9}{{3520}}{x^2} - \frac{{81}}{{44}}x + 840\) với \(0 \le x \le 2000\)
Tìm toạ độ các đỉnh của lát cắt dãy núi trên đoạn [0; 2000]
Phương pháp giải:
Tìm h’(x) và lập bảng biến thiên
Lời giải chi tiết:
Tập xác định: \(D = [0;2000]\)
\(h'(x) = - \frac{1}{{440000}}{x^2} + \frac{9}{{1760}}x - \frac{{81}}{{44}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1800\\x = 450\end{array} \right.\)
Bảng biến thiên:
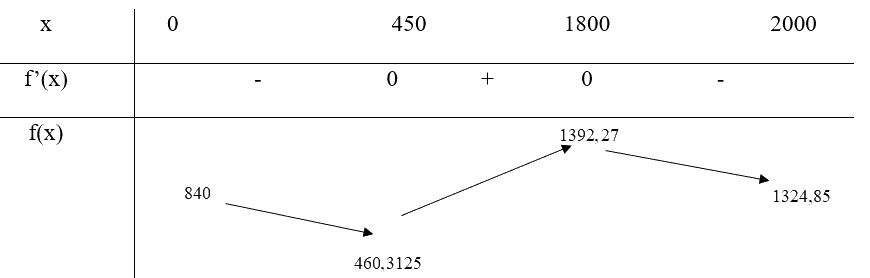
Vậy trên đoạn [0; 2000]:
Tọa độ đỉnh cực tiểu của dãy núi là (450; 460,3125)
Tọa độ đỉnh cực đại của dãy núi là (1800; 1392,27)
Trả lời câu hỏi Khám phá 3 trang 11 SGK Toán 12 Chân trời sáng tạo
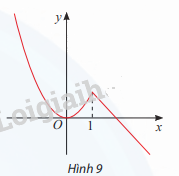
Đồ thị của hàm số \(y = \left\{ \begin{array}{l}{x^2}{\rm{ }}khi{\rm{ }}x \le 1{\rm{ }}\\2 - x{\rm{ }}khi{\rm{ }}x > 1\end{array} \right.\) được cho ở Hình 9.
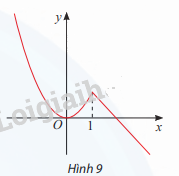
a) Tìm điểm cực đại và điểm cực tiểu của hàm số.
b) Tại x = 1, hàm số có đạo hàm không?
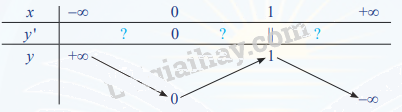
c) Thay mỗi dấu ? bằng kí hiệu (+, –) thích hợp để hoàn thành bảng biến thiên dưới đây. Nhận xét về dấu của y' khi x đi qua điểm cực đại và điểm cực tiểu.
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
a) Hàm số y = f (x) có:
x = 1 là điểm cực đại vì f (x) < f(1) với mọi \(x \in \left( {0;{\rm{ + }}\infty } \right)\backslash \left\{ 0 \right\}\)
x = 0 là điểm cực tiểu vì f(x) > f(0) với mọi \(x \in \left( { + \infty ;{\rm{ 1}}} \right)\backslash \left\{ 0 \right\}\)
b) Tại x = 1, hàm số không có đạo hàm vì đồ thị bị gấp khúc
c)
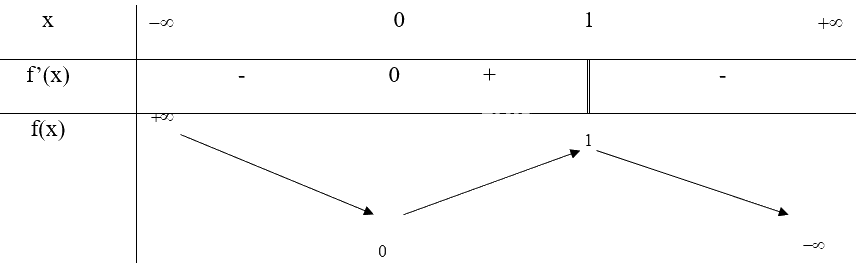
Nhận xét: Khi đi qua các điểm cực đại và cực tiểu thì y’ đổi dấu
Trả lời câu hỏi Khám phá 2 trang 10 SGK Toán 12 Chân trời sáng tạo
Quan sát đồ thị của hàm số \(y = f\left( x \right) = {x^3}--3{x^2} + 1{\rm{ }}\) trong Hình 5.
a) Tìm khoảng (a; b) chứa điểm x = 0 mà trên đó f(x) < f(0) với mọi \(x \ne 0\).
b) Tìm khoảng (a; b) chứa điểm x = 2 mà trên đó f(x) > f(2) với mọi \(x \ne 2\).
c) Tồn tại hay không khoảng (a; b) chứa điểm x = 1 mà trên đó f(x) > f(1) với mọi \(x \ne 1\) hoặc f(x) < f(1) với mọi \(x \ne 1\)?
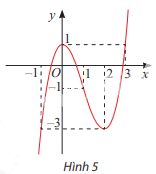
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
a) Trên khoảng (-1; 2), f(x) < f(0) với mọi \(x \ne 0\)
b) Trên khoảng (0; 3), f(x) > f(2) với mọi \(x \ne 2\)
c) Không tồn tại khoảng (a; b) chứa điểm x = 1 mà trên đó f(x) > f(1) với mọi \(x \ne 1\) hoặc f(x) < f(1) với mọi \(x \ne 1\)
Trả lời câu hỏi Thực hành 4 trang 11 SGK Toán 12 Chân trời sáng tạo
Tìm các điểm cực trị của hàm số y = f(x) có đồ thị cho ở Hình 8
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
Hàm số y = f (x) có:
x = 5 là điểm cực đại vì f (x) < f(5) với mọi \(x \in \left( {3;{\rm{ 7}}} \right)\backslash \left\{ 5 \right\}\), \({y_{cd}} = f(5) = 5\)
x = 3 là điểm cực tiểu vì f(x) > f(3) với mọi \(x \in \left( {1;{\rm{ 5}}} \right)\backslash \left\{ 3 \right\}\), \({y_{ct}} = f(3) = 2\)
x=7 là điểm cực tiểu vì f(x) > f(7) với mọi \(x \in \left( {5;{\rm{ 9}}} \right)\backslash \left\{ 7 \right\}\), \({y_{ct}} = f(7) = 1\)
Trả lời câu hỏi Khám phá 3 trang 11 SGK Toán 12 Chân trời sáng tạo
Đồ thị của hàm số \(y = \left\{ \begin{array}{l}{x^2}{\rm{ }}khi{\rm{ }}x \le 1{\rm{ }}\\2 - x{\rm{ }}khi{\rm{ }}x > 1\end{array} \right.\) được cho ở Hình 9.
a) Tìm điểm cực đại và điểm cực tiểu của hàm số.
b) Tại x = 1, hàm số có đạo hàm không?
c) Thay mỗi dấu ? bằng kí hiệu (+, –) thích hợp để hoàn thành bảng biến thiên dưới đây. Nhận xét về dấu của y' khi x đi qua điểm cực đại và điểm cực tiểu.
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
a) Hàm số y = f (x) có:
x = 1 là điểm cực đại vì f (x) < f(1) với mọi \(x \in \left( {0;{\rm{ + }}\infty } \right)\backslash \left\{ 0 \right\}\)
x = 0 là điểm cực tiểu vì f(x) > f(0) với mọi \(x \in \left( { + \infty ;{\rm{ 1}}} \right)\backslash \left\{ 0 \right\}\)
b) Tại x = 1, hàm số không có đạo hàm vì đồ thị bị gấp khúc
c)
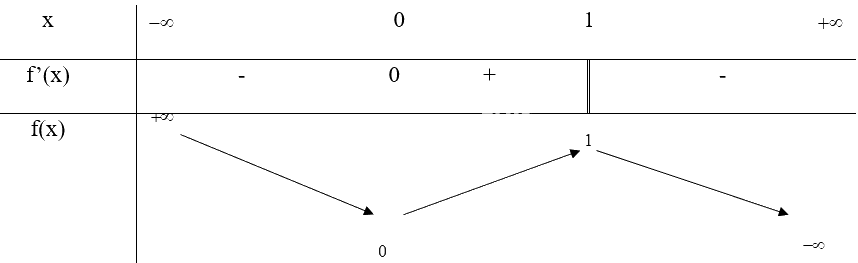
Nhận xét: Khi đi qua các điểm cực đại và cực tiểu thì y’ đổi dấu
Trả lời câu hỏi Thực hành 5 trang 12 SGK Toán 12 Chân trời sáng tạo
Tìm cực trị của hàm số \(g\left( x \right) = \frac{{{x^2} + x + 4}}{{x + 1}}\)
Phương pháp giải:
Tìm tập xác định, g’(x) và lập bảng biến thiên
Lời giải chi tiết:
Tập xác định: \(D = \mathbb{R}\backslash \{ - 1\} \)
\(g'(x) = \frac{{{x^2} + 2x - 3}}{{{x^2} + 2x + 1}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 3\end{array} \right.\)
Bảng biến thiên:
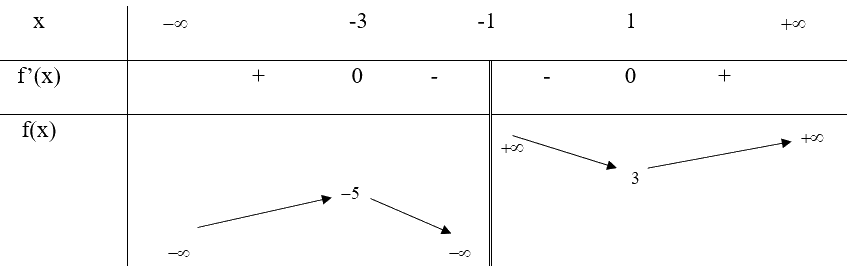
Vậy hàm số đạt cực tiểu tại x = -3, \({y_{ct}} = f( - 3) = - 5\), đạt cực đại tại x = 1, \({y_{cd}} = f(1) = 3\)
Trả lời câu hỏi Vận dụng 2 trang 12 SGK Toán 12 Chân trời sáng tạo
Một phần lát cắt của dãy núi có độ cao tính bằng mét được mô tả bởi hàm số \(y = h\left( x \right) = - \frac{1}{{1320000}}{x^3} + \frac{9}{{3520}}{x^2} - \frac{{81}}{{44}}x + 840\) với \(0 \le x \le 2000\)
Tìm toạ độ các đỉnh của lát cắt dãy núi trên đoạn [0; 2000]
Phương pháp giải:
Tìm h’(x) và lập bảng biến thiên
Lời giải chi tiết:
Tập xác định: \(D = [0;2000]\)
\(h'(x) = - \frac{1}{{440000}}{x^2} + \frac{9}{{1760}}x - \frac{{81}}{{44}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1800\\x = 450\end{array} \right.\)
Bảng biến thiên:
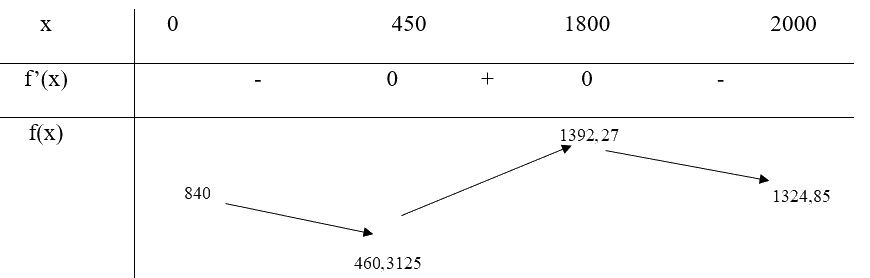
Vậy trên đoạn [0; 2000]:
Tọa độ đỉnh cực tiểu của dãy núi là (450; 460,3125)
Tọa độ đỉnh cực đại của dãy núi là (1800; 1392,27)
Mục 2 của SGK Toán 12 tập 1 chương trình Chân trời sáng tạo tập trung vào các kiến thức cơ bản về giới hạn của hàm số. Đây là một trong những chủ đề quan trọng, nền tảng cho việc học tập các kiến thức nâng cao hơn trong chương trình Toán 12. Việc nắm vững các khái niệm, định lý và kỹ năng giải bài tập liên quan đến giới hạn hàm số là vô cùng cần thiết.
Mục 2 bao gồm các nội dung chính sau:
Trang 10 SGK Toán 12 tập 1 Chân trời sáng tạo chứa các bài tập vận dụng kiến thức về khái niệm giới hạn của hàm số. Các bài tập này thường yêu cầu học sinh:
Ví dụ, bài tập 1 yêu cầu tính giới hạn của hàm số f(x) = (x^2 - 1)/(x - 1) khi x tiến tới 1. Để giải bài tập này, ta có thể phân tích tử số thành nhân tử và rút gọn biểu thức, sau đó thay x = 1 vào biểu thức rút gọn để tìm giới hạn.
Trang 11 tập trung vào các bài tập về giới hạn một bên. Các bài tập này yêu cầu học sinh:
Ví dụ, bài tập 3 yêu cầu tính giới hạn trái và giới hạn phải của hàm số f(x) = |x|/x khi x tiến tới 0. Để giải bài tập này, ta cần xét hai trường hợp: x > 0 và x < 0.
Trang 12 chứa các bài tập tổng hợp về giới hạn hàm số, bao gồm cả các bài tập về giới hạn tại một điểm và giới hạn một bên. Các bài tập này thường có độ khó cao hơn và yêu cầu học sinh phải vận dụng linh hoạt các kiến thức đã học.
Ví dụ, bài tập 5 yêu cầu chứng minh rằng hàm số f(x) = sin(x)/x có giới hạn khi x tiến tới 0. Để chứng minh điều này, ta có thể sử dụng định lý kẹp (squeeze theorem).
Hy vọng với lời giải chi tiết và những lời khuyên trên, các em học sinh sẽ tự tin hơn khi giải các bài tập về giới hạn hàm số trong Mục 2 SGK Toán 12 tập 1 Chân trời sáng tạo. Chúc các em học tập tốt!