Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12 tập 2. Bài viết này sẽ hướng dẫn bạn giải bài tập 8 trang 27 SGK Toán 12 tập 2 theo chương trình Chân trời sáng tạo.
Chúng tôi cam kết cung cấp nội dung chính xác, đầy đủ và giúp bạn nắm vững kiến thức Toán học.
Sử dụng tích phân, tính thể tích của hình chóp tứ giác đều có cạnh đáy bằng (a) và chiều cao bằng (h).
Đề bài
Sử dụng tích phân, tính thể tích của hình chóp tứ giác đều có cạnh đáy bằng \(a\) và chiều cao bằng \(h\).
Phương pháp giải - Xem chi tiết
Chọn trục \(Ox\) sao cho \(O\) trùng với đỉnh của khối chóp.
Dựng một mặt phẳng cắt trục \(Ox\) tại điểm có hoành độ \(x\). Mặt phẳng đó cắt khối chóp \(O.ABCD\) với mặt cắt là hình vuông \(A'B'C'D'\).
Tính độ dài cạnh \(A'B'\), sau đó tính diện tích mặt cắt \(S\left( x \right) = {S_{A'B'C'D'}}\), từ đó tính thể tích khối chóp tứ giác đều \(O.ABCD\) theo công thức \(V = \int\limits_0^h {S\left( x \right)dx} \).
Lời giải chi tiết
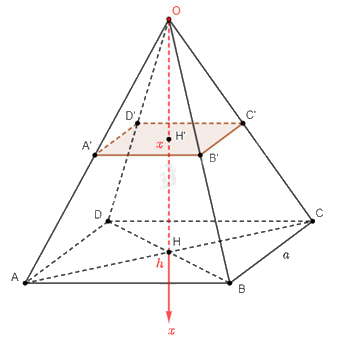
Xét khối chóp đều \(O.ABCD\) có chiều cao \(OH = h\), độ dài cạnh đáy \(AB = a\)
Chọn trục \(Ox\) sao cho \(O\) trùng với đỉnh của khối chóp, mặt đáy \(\left( {ABCD} \right)\) cắt trục \(Ox\) tại điểm có hoành độ \(\) như hình vẽ.
Dựng một mặt phẳng cắt trục \(Ox\) tại điểm có hoành độ \(x\). Mặt phẳng đó cắt khối chóp \(O.ABCD\) với mặt cắt là hình vuông \(A'B'C'D'\).
Ta có \(\frac{{B'C'}}{{BC}} = \frac{{OB'}}{{OB}} = \frac{{OH'}}{{OH}} = \frac{x}{h} \Rightarrow B'C' = \frac{a}{h}x\).
Diện tích mặt cắt \(A'B'C'D'\) là \(S\left( x \right) = {\left( {\frac{a}{h}x} \right)^2} = \frac{{{a^2}}}{{{h^2}}}{x^2}\).
Vậy thể tích khối chóp đều \(O.ABCD\) là \(V = \int\limits_0^h {\left( {\frac{{{a^2}}}{{{h^2}}}{x^2}} \right)dx} = \frac{{{a^2}}}{{{h^2}}}\left. {\left( {\frac{{{x^3}}}{3}} \right)} \right|_0^h = \frac{{{a^2}}}{{{h^2}}}.\frac{{{h^3}}}{3} = \frac{{{a^2}h}}{3}\)
Bài tập 8 trang 27 SGK Toán 12 tập 2 thuộc chương trình Chân trời sáng tạo, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến tốc độ thay đổi của một đại lượng. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm như đạo hàm, quy tắc tính đạo hàm, và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Bài tập 8 thường bao gồm các dạng bài sau:
Để giúp các bạn học sinh giải bài tập 8 trang 27 SGK Toán 12 tập 2 một cách hiệu quả, chúng tôi xin trình bày lời giải chi tiết cho từng câu hỏi:
Cho hàm số y = x3 - 3x2 + 2. Hãy tính đạo hàm của hàm số.
Lời giải:
y' = 3x2 - 6x
Tìm cực trị của hàm số y = x3 - 3x2 + 2.
Lời giải:
y' = 3x2 - 6x
Giải phương trình y' = 0, ta được x = 0 hoặc x = 2.
Xét dấu đạo hàm, ta thấy:
Vậy hàm số đạt cực đại tại x = 0, ymax = 2 và đạt cực tiểu tại x = 2, ymin = -2.
Để giải các bài tập về đạo hàm một cách hiệu quả, bạn nên:
Ngoài SGK Toán 12 tập 2, bạn có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập hiệu quả mà chúng tôi đã cung cấp, các bạn học sinh sẽ tự tin hơn khi giải bài tập 8 trang 27 SGK Toán 12 tập 2 - Chân trời sáng tạo. Chúc các bạn học tập tốt!