Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 2 của giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 12 tập 2, chương trình Chân trời sáng tạo.
Ở bài viết này, chúng ta sẽ cùng nhau giải quyết các bài tập trong mục 1 trang 44, 45, 46, 47. Mục tiêu là giúp các em nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong các kỳ thi sắp tới.
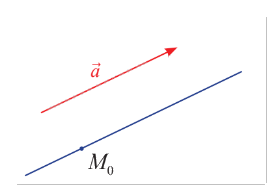
Trong không gian \(Oxyz\), cho điểm \({M_0}\) cố định và vectơ \(\vec a\) khác \(\vec 0\). Có bao nhiêu đường thẳng \(d\) đi qua \({M_0}\) và song song hoặc trùng với giá của \(\vec a\)?
Trả lời câu hỏi Thực hành 2 trang 46 SGK Toán 12 Chân trời sáng tạo
Cho đường thẳng \(d\) có phương trình tham số \(\left\{ \begin{array}{l}x = - 1 + 8t\\y = - 4t\\z = 3 + 12t\end{array} \right.\)
a) Tìm hai vectơ chỉ phương của \(d.\)
b) Tìm ba điểm trên \(d.\)
Phương pháp giải:
a) Từ phương trình tham số, chỉ ra hai vectơ chỉ phương của đường thẳng.
b) Từ phương trình tham số, chỉ ra ba điểm nằm trên đường thẳng.
Lời giải chi tiết:
a) Từ phương trình tham số, ta có \(\vec a = \left( {8; - 4;12} \right)\) là một vectơ chỉ phương của đường thẳng \(d.\)
Chọn \(\vec b = \frac{1}{4}\vec a = \left( {2; - 1;3} \right)\), ta có \(\vec b\) cũng là một vectơ chỉ phương của đường thẳng \(d.\)
b) Thay \(t = 0\) vào phương trình tham số của \(d\), ta được \(\left\{ \begin{array}{l}x = - 1 + 8.0\\y = - 4.0\\z = 3 + 12.0\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = - 1\\y = 0\\z = 3\end{array} \right.\)
Vậy \(A\left( { - 1;0;3} \right)\) là một điểm nằm trên đường thẳng \(d.\)
Thay \(t = 1\) vào phương trình tham số của \(d\), ta được \(\left\{ \begin{array}{l}x = - 1 + 8.1\\y = - 4.1\\z = 3 + 12.1\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = 7\\y = - 4\\z = 15\end{array} \right.\)
Vậy \(B\left( {7; - 4;15} \right)\) là một điểm nằm trên đường thẳng \(d.\)
Thay \(t = 2\) vào phương trình tham số của \(d\), ta được \(\left\{ \begin{array}{l}x = - 1 + 8.2\\y = - 4.2\\z = 3 + 12.2\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = 15\\y = - 8\\z = 27\end{array} \right.\)
Vậy \(C\left( {15; - 8;27} \right)\) là một điểm nằm trên đường thẳng \(d.\)
Trả lời câu hỏi Thực hành 3 trang 46 SGK Toán 12 Chân trời sáng tạo
Viết phương trình tham số của đường thẳng \(d\) đi qua điểm \(A\left( {5;0; - 7} \right)\) và nhận \(\vec v = \left( {9;0; - 2} \right)\) làm vectơ chỉ phương. Đường thẳng \(d\) có đi qua điểm \(M\left( { - 4;0; - 5} \right)\) không?
Phương pháp giải:
Viết phương trình đường thẳng \(d.\)
Để kiểm tra điểm \(M\) có nằm trên đường thẳng \(d\) hay không, thực hiện thay hoành độ của điểm \(M\) vào phương trình để tìm tham số \(t\), sau đó thay tung độ và cao độ của \(z\) vào các phương trình còn lại để kiểm tra xem phương trình có thoả mãn hay không.
Lời giải chi tiết:
Phương trình tham số của \(d\) là \(\left\{ \begin{array}{l}x = 5 + 9t\\y = 0\\z = - 7 - 2t\end{array} \right.\)
Thay hoành độ điểm \(M\) vào phương trình \(x = 5 + 9t\), ta được \( - 4 = 5 + 9t\), suy ra \(t = - 1.\)
Thay \(t = - 1\), tung độ và cao độ của điểm \(M\) vào các phương trình còn lại, ta thấy các phương trình đó thoả mãn (do \(0 = 0\) và \( - 5 = - 7 - 2.\left( { - 1} \right)\)).
Vậy đường thẳng \(d\) đi qua điểm \(M.\)
Trả lời câu hỏi Hoạt động 3 trang 46 SGK Toán 12 Chân trời sáng tạo
Cho đường thẳng \(d\) có phương trình tham số \(\left\{ \begin{array}{l}x = {x_0} + {a_1}t\\y = {y_0} + {a_2}t\\z = {z_0} + {a_3}t\end{array} \right.\) với \({a_1}\), \({a_2}\), \({a_3}\) đều khác 0. Lấy điểm \(M\left( {x;y;z} \right)\) bất kì thuộc \(d\). So sánh các biểu thức \(\frac{{x - {x_0}}}{{{a_1}}}\); \(\frac{{y - {y_0}}}{{{a_2}}}\); \(\frac{{z - {z_0}}}{{{a_3}}}.\)
Phương pháp giải:
Lần lượt tính các biểu thức \(\frac{{x - {x_0}}}{{{a_1}}}\); \(\frac{{y - {y_0}}}{{{a_2}}}\); \(\frac{{z - {z_0}}}{{{a_3}}}\) và so sánh các kết quả.
Lời giải chi tiết:
Ta có \(M\left( {x;y;z} \right)\) thuộc \(d\), nên ta có \(\left\{ \begin{array}{l}x = {x_0} + {a_1}t\\y = {y_0} + {a_2}t\\z = {z_0} + {a_3}t\end{array} \right.\)
Suy ra \(\frac{{x - {x_0}}}{{{a_1}}} = t\); \(\frac{{y - {y_0}}}{{{a_2}}} = t\); \(\frac{{z - {z_0}}}{{{a_3}}} = t.\)
Như vậy \(\frac{{x - {x_0}}}{{{a_1}}} = \frac{{y - {y_0}}}{{{a_2}}} = \frac{{z - {z_0}}}{{{a_3}}}.\)
Trả lời câu hỏi Thực hành 4 trang 46 SGK Toán 12 Chân trời sáng tạo
Viết phương trình chính tắc của đường thẳng \(d\) đi qua điểm \({M_0}\left( {5;0; - 6} \right)\) và nhận \(\vec a = \left( {3;2; - 4} \right)\) làm vectơ chỉ phương.
Phương pháp giải:
Phương trình chính tắc của đường thẳng \(d\) đi qua điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) và nhận \(\vec a = \left( {{a_1};{a_2};{a_3}} \right)\) làm vectơ chỉ phương là \(\frac{{x - {x_0}}}{{{a_1}}} = \frac{{y - {y_0}}}{{{a_2}}} = \frac{{z - {z_0}}}{{{a_3}}}.\)
Lời giải chi tiết:
Phương trình chính tắc của đường thẳng \(d\) đi qua điểm \({M_0}\left( {5;0; - 6} \right)\) và nhận \(\vec a = \left( {3;2; - 4} \right)\) làm vectơ chỉ phương là \(\frac{{x - 5}}{3} = \frac{{y - 0}}{2} = \frac{{z - \left( { - 6} \right)}}{{ - 4}}\) hay \(\frac{{x - 5}}{3} = \frac{y}{2} = \frac{{z + 6}}{{ - 4}}.\)
Trả lời câu hỏi Hoạt động 4 trang 47 SGK Toán 12 Chân trời sáng tạo
Cho đường thẳng \(d\) đi qua hai điểm \(A\left( {2;2;1} \right)\) và \(B\left( {4;5;3} \right).\)
a) Tìm một vectơ chỉ phương của \(d.\)
b) Viết phương trình tham số và phương trình chính tắc của \(d.\)
Phương pháp giải:
a) Đường thẳng \(d\) đi qua hai điểm \(A\) và \(B\) nên nó nhận \(\overrightarrow {AB} \) là một vectơ chỉ phương.
b) Viết phương trình đường thẳng \(d\) đi qua \(A\) và có một vectơ chỉ phương là \(\overrightarrow {AB} .\)
Lời giải chi tiết:
a) Đường thẳng \(d\) đi qua hai điểm \(A\left( {2;2;1} \right)\) và \(B\left( {4;5;3} \right)\) nên nó nhận \(\overrightarrow {AB} \left( {2;3;2} \right)\) là một vectơ chỉ phương.
b) Phương trình tham số của đường thẳng \(d\) đi qua \(A\left( {2;2;1} \right)\) và có một vectơ chỉ phương \(\overrightarrow {AB} \left( {2;3;2} \right)\) là \(\left\{ \begin{array}{l}x = 2 + 2t\\y = 2 + 3t\\z = 1 + 2t\end{array} \right.\)
Phương trình chính tắc của đường thẳng \(d\) đi qua \(A\left( {2;2;1} \right)\) và có một vectơ chỉ phương \(\overrightarrow {AB} \left( {2;3;2} \right)\) là \(\frac{{x - 2}}{2} = \frac{{y - 2}}{3} = \frac{{z - 1}}{2}.\)
Trả lời câu hỏi Thực hành 5 trang 47 SGK Toán 12 Chân trời sáng tạo
Viết phương trình tham số và phương trình chính tắc của đường thẳng \(MN\), biết \(M\left( {2;0; - 1} \right)\) và \(N\left( {4;3;1} \right).\)
Phương pháp giải:
Đường thẳng \(MN\) đi qua hai điểm \(M\) và \(N\) nên \(\overrightarrow {MN} \) là một vectơ chỉ phương của đường thẳng, từ đó viết được phương trình tham số và phương trình chính tắc của đường thẳng \(MN.\)
Lời giải chi tiết:
Ta có \(\overrightarrow {MN} = \left( {2;3;2} \right)\).
Đường thẳng \(MN\) đi qua điểm \(M\left( {2;0; - 1} \right)\) và có một vectơ chỉ phương là \(\overrightarrow {MN} = \left( {2;3;2} \right)\) nên phương trình tham số của đường thẳng \(MN\) là \(\left\{ \begin{array}{l}x = 2 + 2t\\y = 0 + 3t\\z = - 1 + 2t\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = 2 + 2t\\y = 3t\\z = - 1 + 2t\end{array} \right.\); phương trình chính tắc của đường thẳng \(MN\) là \(\frac{{x - 2}}{2} = \frac{{y - 0}}{3} = \frac{{z + 1}}{2}\) hay \(\frac{{x - 2}}{2} = \frac{y}{3} = \frac{{z + 1}}{2}.\)
Trả lời câu hỏi Thực hành 1 trang 44 SGK Toán 12 Chân trời sáng tạo
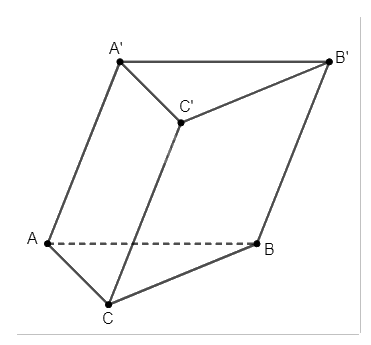
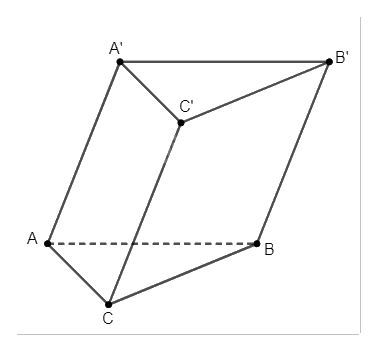
Trong không gian \(Oxyz\), cho hình lăng trụ tam giác \(ABC.A'B'C'\) với \(A\left( {1;2;1} \right)\), \(B\left( {7;5;3} \right)\), \(C\left( {4;2;0} \right)\), \(A'\left( {4;9;9} \right)\). Tìm toạ độ một vectơ chỉ phương của mỗi đường thẳng \(AB\), \(A'C'\) và \(BB'.\)
Phương pháp giải:
Các đường thẳng \(AB\), \(A'C'\) và \(BB'\) có một vectơ chỉ phương lần lượt là \(\overrightarrow {AB} \), \(\overrightarrow {AC} \) và \(\overrightarrow {AA'} .\)
Lời giải chi tiết:
Ta có \(\overrightarrow {AB} \left( {6;3;2} \right)\) là một vectơ chỉ phương của đường thẳng \(AB.\)
Ta có \(AC\parallel A'C'\) nên \(\overrightarrow {AC} \left( {3;0; - 1} \right)\) là một vectơ chỉ phương của đường thẳng \(A'C'.\)
Ta có \(AA'\parallel BB'\) nên \(\overrightarrow {AA'} \left( {3;7;8} \right)\) là một vectơ chỉ phương của đường thẳng \(BB'.\)
Trả lời câu hỏi Hoạt động 1 trang 44 SGK Toán 12 Chân trời sáng tạo
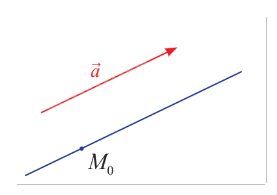
Trong không gian \(Oxyz\), cho điểm \({M_0}\) cố định và vectơ \(\vec a\) khác \(\vec 0\). Có bao nhiêu đường thẳng \(d\) đi qua \({M_0}\) và song song hoặc trùng với giá của \(\vec a\)?
Phương pháp giải:
Trong không gian, qua một điểm không nằm trên một đường thẳng, có duy nhất một đường thẳng đi qua điểm và song song với đường thẳng đó.
Lời giải chi tiết:
Nếu điểm \({M_0}\) nằm trên giá của vectơ \(\vec a\), thì đường thẳng đó là đường thẳng duy nhất cần tìm.
Nếu điểm \({M_0}\) không nằm trên giá của vectơ \(\vec a\), do trong không gian, qua một điểm không nằm trên một đường thẳng, có duy nhất một đường thẳng đi qua điểm và song song với đường thẳng đó, nên tồn tại duy nhất một đường thẳng đi qua \({M_0}\) và song song với giá của vectơ \(\vec a\).
Như vậy, có duy nhất một đường thẳng \(d\) đi qua \({M_0}\) và song song hoặc trùng với giá của \(\vec a.\)
Trả lời câu hỏi Hoạt động 2 trang 44 SGK Toán 12 Chân trời sáng tạo
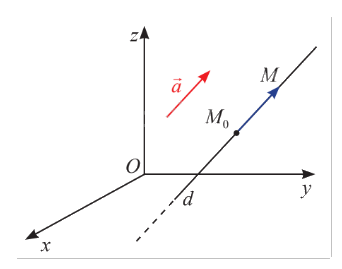
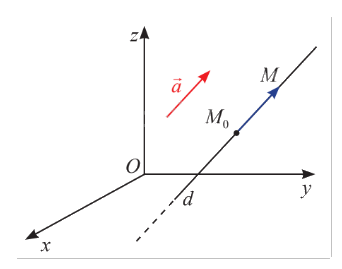
Trong không gian \(Oxyz\), cho đường thẳng \(d\) đi qua điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) cố định và có vectơ chỉ phương là \(\vec a = \left( {{a_1};{a_2};{a_3}} \right)\) khác \(\vec 0.\)
a) Giải thích tại sao ta có thể viết \(M \in d \Leftrightarrow \overrightarrow {{M_0}M} = t\vec a{\rm{ }}\left( {t \in \mathbb{R}} \right).\)
b) Với \(M\left( {x;y;z} \right)\) thuộc \(d\), hãy tính \(x\), \(y\), \(z\) theo \({x_0}\), \({y_0}\), \({z_0}\) và \({a_1}\), \({a_2}\), \({a_3}.\)
Phương pháp giải:
a) Chỉ ra rằng \(\overrightarrow {{M_0}M} \) và \(\vec a\) là hai vectơ cùng phương.
b) Sử dụng tính chất của hai vectơ cùng phương.
Lời giải chi tiết:
a) Ta có \(\vec a\) là vectơ chỉ phương của đường thẳng \(d\).
Nếu \(M \in d\), ta có \(d\) đi qua hai điểm \(M\) và \({M_0}\) nên hai vectơ \(\overrightarrow {{M_0}M} \) và \(\vec a\) là hai vectơ cùng phương, suy ra \(\overrightarrow {{M_0}M} = t\vec a\) với \(t \in \mathbb{R}\).
Ngược lại, với \(\overrightarrow {{M_0}M} = t\vec a\) thì \(\overrightarrow {{M_0}M} \) và \(\vec a\) là hai vectơ cùng phương. Mà \(\vec a\) là vectơ chỉ phương của đường thẳng \(d\), nên \(\overrightarrow {{M_0}M} \) cũng là một vectơ chỉ phương của đường thẳng \(d\). Do \({M_0} \in d\), nên ta suy ra \(M \in d\).
b) Ta có \(\overrightarrow {{M_0}M} = \left( {x - {x_0};y - {y_0};z - {z_0}} \right)\) và \(\vec a = \left( {{a_1};{a_2};{a_3}} \right)\).
Theo câu a, ta có \(\overrightarrow {{M_0}M} = t\vec a\) nên \(\left( {x - {x_0};y - {y_0};z - {z_0}} \right) = t\left( {{a_1};{a_2};{a_3}} \right)\)
Suy ra \(\left\{ \begin{array}{l}x - {x_0} = t{a_1}\\y - {y_0} = t{a_2}\\z - {z_0} = t{a_3}\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = {x_0} + t{a_1}\\y = {y_0} + t{a_2}\\z = {z_0} + t{a_3}\end{array} \right.\)
Trả lời câu hỏi Vận dụng 1 trang 47 SGK Toán 12 Chân trời sáng tạo
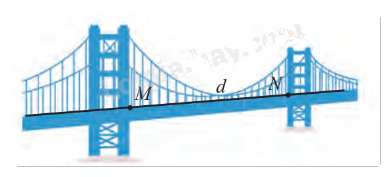
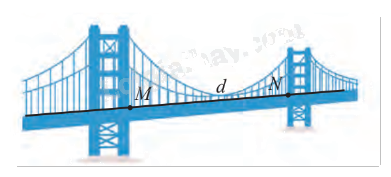
Một mô hình cầu treo được thiết kế trong không gian \(Oxyz\) như hình dưới đây. Viết phương trình tham số của làn đường \(d\) đi qua hai điểm \(M\left( {4;3;20} \right)\) và \(N\left( {4;1000;20} \right).\)
Phương pháp giải:
Đường thẳng \(d\) đi qua hai điểm \(M\) và \(N\) nên \(\overrightarrow {MN} \) là một vectơ chỉ phương của đường thẳng, từ đó viết được phương trình tham số của \(d.\)
Lời giải chi tiết:
Ta có \(\overrightarrow {MN} = \left( {0;997;0} \right)\).
Đường thẳng \(d\) đi qua hai điểm \(M\) và \(N\) nên \(\overrightarrow {MN} \) là một vectơ chỉ phương của đường thẳng. Suy ra vectơ \(\vec u = \frac{1}{{997}}\overrightarrow {MN} = \left( {0;1;0} \right)\) cũng là một vectơ chỉ phương của đường thẳng \(d.\)
Phương trình tham số của làn đường \(d\) đi qua \(M\left( {4;3;20} \right)\) và có một vectơ chỉ phương \(\vec u = \left( {0;1;0} \right)\) là \(\left\{ \begin{array}{l}x = 4 + 0t\\y = 3 + t\\z = 20 + 0t\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = 4\\y = 3 + t\\z = 20\end{array} \right.\).
Đặt \(t' = t + 3\), phương trình tham số của làn đường \(d\) là \(\left\{ \begin{array}{l}x = 4\\y = t'\\z = 20\end{array} \right.\).
Trả lời câu hỏi Hoạt động 1 trang 44 SGK Toán 12 Chân trời sáng tạo
Trong không gian \(Oxyz\), cho điểm \({M_0}\) cố định và vectơ \(\vec a\) khác \(\vec 0\). Có bao nhiêu đường thẳng \(d\) đi qua \({M_0}\) và song song hoặc trùng với giá của \(\vec a\)?
Phương pháp giải:
Trong không gian, qua một điểm không nằm trên một đường thẳng, có duy nhất một đường thẳng đi qua điểm và song song với đường thẳng đó.
Lời giải chi tiết:
Nếu điểm \({M_0}\) nằm trên giá của vectơ \(\vec a\), thì đường thẳng đó là đường thẳng duy nhất cần tìm.
Nếu điểm \({M_0}\) không nằm trên giá của vectơ \(\vec a\), do trong không gian, qua một điểm không nằm trên một đường thẳng, có duy nhất một đường thẳng đi qua điểm và song song với đường thẳng đó, nên tồn tại duy nhất một đường thẳng đi qua \({M_0}\) và song song với giá của vectơ \(\vec a\).
Như vậy, có duy nhất một đường thẳng \(d\) đi qua \({M_0}\) và song song hoặc trùng với giá của \(\vec a.\)
Trả lời câu hỏi Thực hành 1 trang 44 SGK Toán 12 Chân trời sáng tạo
Trong không gian \(Oxyz\), cho hình lăng trụ tam giác \(ABC.A'B'C'\) với \(A\left( {1;2;1} \right)\), \(B\left( {7;5;3} \right)\), \(C\left( {4;2;0} \right)\), \(A'\left( {4;9;9} \right)\). Tìm toạ độ một vectơ chỉ phương của mỗi đường thẳng \(AB\), \(A'C'\) và \(BB'.\)
Phương pháp giải:
Các đường thẳng \(AB\), \(A'C'\) và \(BB'\) có một vectơ chỉ phương lần lượt là \(\overrightarrow {AB} \), \(\overrightarrow {AC} \) và \(\overrightarrow {AA'} .\)
Lời giải chi tiết:
Ta có \(\overrightarrow {AB} \left( {6;3;2} \right)\) là một vectơ chỉ phương của đường thẳng \(AB.\)
Ta có \(AC\parallel A'C'\) nên \(\overrightarrow {AC} \left( {3;0; - 1} \right)\) là một vectơ chỉ phương của đường thẳng \(A'C'.\)
Ta có \(AA'\parallel BB'\) nên \(\overrightarrow {AA'} \left( {3;7;8} \right)\) là một vectơ chỉ phương của đường thẳng \(BB'.\)
Trả lời câu hỏi Hoạt động 2 trang 44 SGK Toán 12 Chân trời sáng tạo
Trong không gian \(Oxyz\), cho đường thẳng \(d\) đi qua điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) cố định và có vectơ chỉ phương là \(\vec a = \left( {{a_1};{a_2};{a_3}} \right)\) khác \(\vec 0.\)
a) Giải thích tại sao ta có thể viết \(M \in d \Leftrightarrow \overrightarrow {{M_0}M} = t\vec a{\rm{ }}\left( {t \in \mathbb{R}} \right).\)
b) Với \(M\left( {x;y;z} \right)\) thuộc \(d\), hãy tính \(x\), \(y\), \(z\) theo \({x_0}\), \({y_0}\), \({z_0}\) và \({a_1}\), \({a_2}\), \({a_3}.\)
Phương pháp giải:
a) Chỉ ra rằng \(\overrightarrow {{M_0}M} \) và \(\vec a\) là hai vectơ cùng phương.
b) Sử dụng tính chất của hai vectơ cùng phương.
Lời giải chi tiết:
a) Ta có \(\vec a\) là vectơ chỉ phương của đường thẳng \(d\).
Nếu \(M \in d\), ta có \(d\) đi qua hai điểm \(M\) và \({M_0}\) nên hai vectơ \(\overrightarrow {{M_0}M} \) và \(\vec a\) là hai vectơ cùng phương, suy ra \(\overrightarrow {{M_0}M} = t\vec a\) với \(t \in \mathbb{R}\).
Ngược lại, với \(\overrightarrow {{M_0}M} = t\vec a\) thì \(\overrightarrow {{M_0}M} \) và \(\vec a\) là hai vectơ cùng phương. Mà \(\vec a\) là vectơ chỉ phương của đường thẳng \(d\), nên \(\overrightarrow {{M_0}M} \) cũng là một vectơ chỉ phương của đường thẳng \(d\). Do \({M_0} \in d\), nên ta suy ra \(M \in d\).
b) Ta có \(\overrightarrow {{M_0}M} = \left( {x - {x_0};y - {y_0};z - {z_0}} \right)\) và \(\vec a = \left( {{a_1};{a_2};{a_3}} \right)\).
Theo câu a, ta có \(\overrightarrow {{M_0}M} = t\vec a\) nên \(\left( {x - {x_0};y - {y_0};z - {z_0}} \right) = t\left( {{a_1};{a_2};{a_3}} \right)\)
Suy ra \(\left\{ \begin{array}{l}x - {x_0} = t{a_1}\\y - {y_0} = t{a_2}\\z - {z_0} = t{a_3}\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = {x_0} + t{a_1}\\y = {y_0} + t{a_2}\\z = {z_0} + t{a_3}\end{array} \right.\)
Trả lời câu hỏi Thực hành 2 trang 46 SGK Toán 12 Chân trời sáng tạo
Cho đường thẳng \(d\) có phương trình tham số \(\left\{ \begin{array}{l}x = - 1 + 8t\\y = - 4t\\z = 3 + 12t\end{array} \right.\)
a) Tìm hai vectơ chỉ phương của \(d.\)
b) Tìm ba điểm trên \(d.\)
Phương pháp giải:
a) Từ phương trình tham số, chỉ ra hai vectơ chỉ phương của đường thẳng.
b) Từ phương trình tham số, chỉ ra ba điểm nằm trên đường thẳng.
Lời giải chi tiết:
a) Từ phương trình tham số, ta có \(\vec a = \left( {8; - 4;12} \right)\) là một vectơ chỉ phương của đường thẳng \(d.\)
Chọn \(\vec b = \frac{1}{4}\vec a = \left( {2; - 1;3} \right)\), ta có \(\vec b\) cũng là một vectơ chỉ phương của đường thẳng \(d.\)
b) Thay \(t = 0\) vào phương trình tham số của \(d\), ta được \(\left\{ \begin{array}{l}x = - 1 + 8.0\\y = - 4.0\\z = 3 + 12.0\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = - 1\\y = 0\\z = 3\end{array} \right.\)
Vậy \(A\left( { - 1;0;3} \right)\) là một điểm nằm trên đường thẳng \(d.\)
Thay \(t = 1\) vào phương trình tham số của \(d\), ta được \(\left\{ \begin{array}{l}x = - 1 + 8.1\\y = - 4.1\\z = 3 + 12.1\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = 7\\y = - 4\\z = 15\end{array} \right.\)
Vậy \(B\left( {7; - 4;15} \right)\) là một điểm nằm trên đường thẳng \(d.\)
Thay \(t = 2\) vào phương trình tham số của \(d\), ta được \(\left\{ \begin{array}{l}x = - 1 + 8.2\\y = - 4.2\\z = 3 + 12.2\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = 15\\y = - 8\\z = 27\end{array} \right.\)
Vậy \(C\left( {15; - 8;27} \right)\) là một điểm nằm trên đường thẳng \(d.\)
Trả lời câu hỏi Thực hành 3 trang 46 SGK Toán 12 Chân trời sáng tạo
Viết phương trình tham số của đường thẳng \(d\) đi qua điểm \(A\left( {5;0; - 7} \right)\) và nhận \(\vec v = \left( {9;0; - 2} \right)\) làm vectơ chỉ phương. Đường thẳng \(d\) có đi qua điểm \(M\left( { - 4;0; - 5} \right)\) không?
Phương pháp giải:
Viết phương trình đường thẳng \(d.\)
Để kiểm tra điểm \(M\) có nằm trên đường thẳng \(d\) hay không, thực hiện thay hoành độ của điểm \(M\) vào phương trình để tìm tham số \(t\), sau đó thay tung độ và cao độ của \(z\) vào các phương trình còn lại để kiểm tra xem phương trình có thoả mãn hay không.
Lời giải chi tiết:
Phương trình tham số của \(d\) là \(\left\{ \begin{array}{l}x = 5 + 9t\\y = 0\\z = - 7 - 2t\end{array} \right.\)
Thay hoành độ điểm \(M\) vào phương trình \(x = 5 + 9t\), ta được \( - 4 = 5 + 9t\), suy ra \(t = - 1.\)
Thay \(t = - 1\), tung độ và cao độ của điểm \(M\) vào các phương trình còn lại, ta thấy các phương trình đó thoả mãn (do \(0 = 0\) và \( - 5 = - 7 - 2.\left( { - 1} \right)\)).
Vậy đường thẳng \(d\) đi qua điểm \(M.\)
Trả lời câu hỏi Hoạt động 3 trang 46 SGK Toán 12 Chân trời sáng tạo
Cho đường thẳng \(d\) có phương trình tham số \(\left\{ \begin{array}{l}x = {x_0} + {a_1}t\\y = {y_0} + {a_2}t\\z = {z_0} + {a_3}t\end{array} \right.\) với \({a_1}\), \({a_2}\), \({a_3}\) đều khác 0. Lấy điểm \(M\left( {x;y;z} \right)\) bất kì thuộc \(d\). So sánh các biểu thức \(\frac{{x - {x_0}}}{{{a_1}}}\); \(\frac{{y - {y_0}}}{{{a_2}}}\); \(\frac{{z - {z_0}}}{{{a_3}}}.\)
Phương pháp giải:
Lần lượt tính các biểu thức \(\frac{{x - {x_0}}}{{{a_1}}}\); \(\frac{{y - {y_0}}}{{{a_2}}}\); \(\frac{{z - {z_0}}}{{{a_3}}}\) và so sánh các kết quả.
Lời giải chi tiết:
Ta có \(M\left( {x;y;z} \right)\) thuộc \(d\), nên ta có \(\left\{ \begin{array}{l}x = {x_0} + {a_1}t\\y = {y_0} + {a_2}t\\z = {z_0} + {a_3}t\end{array} \right.\)
Suy ra \(\frac{{x - {x_0}}}{{{a_1}}} = t\); \(\frac{{y - {y_0}}}{{{a_2}}} = t\); \(\frac{{z - {z_0}}}{{{a_3}}} = t.\)
Như vậy \(\frac{{x - {x_0}}}{{{a_1}}} = \frac{{y - {y_0}}}{{{a_2}}} = \frac{{z - {z_0}}}{{{a_3}}}.\)
Trả lời câu hỏi Thực hành 4 trang 46 SGK Toán 12 Chân trời sáng tạo
Viết phương trình chính tắc của đường thẳng \(d\) đi qua điểm \({M_0}\left( {5;0; - 6} \right)\) và nhận \(\vec a = \left( {3;2; - 4} \right)\) làm vectơ chỉ phương.
Phương pháp giải:
Phương trình chính tắc của đường thẳng \(d\) đi qua điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) và nhận \(\vec a = \left( {{a_1};{a_2};{a_3}} \right)\) làm vectơ chỉ phương là \(\frac{{x - {x_0}}}{{{a_1}}} = \frac{{y - {y_0}}}{{{a_2}}} = \frac{{z - {z_0}}}{{{a_3}}}.\)
Lời giải chi tiết:
Phương trình chính tắc của đường thẳng \(d\) đi qua điểm \({M_0}\left( {5;0; - 6} \right)\) và nhận \(\vec a = \left( {3;2; - 4} \right)\) làm vectơ chỉ phương là \(\frac{{x - 5}}{3} = \frac{{y - 0}}{2} = \frac{{z - \left( { - 6} \right)}}{{ - 4}}\) hay \(\frac{{x - 5}}{3} = \frac{y}{2} = \frac{{z + 6}}{{ - 4}}.\)
Trả lời câu hỏi Hoạt động 4 trang 47 SGK Toán 12 Chân trời sáng tạo
Cho đường thẳng \(d\) đi qua hai điểm \(A\left( {2;2;1} \right)\) và \(B\left( {4;5;3} \right).\)
a) Tìm một vectơ chỉ phương của \(d.\)
b) Viết phương trình tham số và phương trình chính tắc của \(d.\)
Phương pháp giải:
a) Đường thẳng \(d\) đi qua hai điểm \(A\) và \(B\) nên nó nhận \(\overrightarrow {AB} \) là một vectơ chỉ phương.
b) Viết phương trình đường thẳng \(d\) đi qua \(A\) và có một vectơ chỉ phương là \(\overrightarrow {AB} .\)
Lời giải chi tiết:
a) Đường thẳng \(d\) đi qua hai điểm \(A\left( {2;2;1} \right)\) và \(B\left( {4;5;3} \right)\) nên nó nhận \(\overrightarrow {AB} \left( {2;3;2} \right)\) là một vectơ chỉ phương.
b) Phương trình tham số của đường thẳng \(d\) đi qua \(A\left( {2;2;1} \right)\) và có một vectơ chỉ phương \(\overrightarrow {AB} \left( {2;3;2} \right)\) là \(\left\{ \begin{array}{l}x = 2 + 2t\\y = 2 + 3t\\z = 1 + 2t\end{array} \right.\)
Phương trình chính tắc của đường thẳng \(d\) đi qua \(A\left( {2;2;1} \right)\) và có một vectơ chỉ phương \(\overrightarrow {AB} \left( {2;3;2} \right)\) là \(\frac{{x - 2}}{2} = \frac{{y - 2}}{3} = \frac{{z - 1}}{2}.\)
Trả lời câu hỏi Thực hành 5 trang 47 SGK Toán 12 Chân trời sáng tạo
Viết phương trình tham số và phương trình chính tắc của đường thẳng \(MN\), biết \(M\left( {2;0; - 1} \right)\) và \(N\left( {4;3;1} \right).\)
Phương pháp giải:
Đường thẳng \(MN\) đi qua hai điểm \(M\) và \(N\) nên \(\overrightarrow {MN} \) là một vectơ chỉ phương của đường thẳng, từ đó viết được phương trình tham số và phương trình chính tắc của đường thẳng \(MN.\)
Lời giải chi tiết:
Ta có \(\overrightarrow {MN} = \left( {2;3;2} \right)\).
Đường thẳng \(MN\) đi qua điểm \(M\left( {2;0; - 1} \right)\) và có một vectơ chỉ phương là \(\overrightarrow {MN} = \left( {2;3;2} \right)\) nên phương trình tham số của đường thẳng \(MN\) là \(\left\{ \begin{array}{l}x = 2 + 2t\\y = 0 + 3t\\z = - 1 + 2t\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = 2 + 2t\\y = 3t\\z = - 1 + 2t\end{array} \right.\); phương trình chính tắc của đường thẳng \(MN\) là \(\frac{{x - 2}}{2} = \frac{{y - 0}}{3} = \frac{{z + 1}}{2}\) hay \(\frac{{x - 2}}{2} = \frac{y}{3} = \frac{{z + 1}}{2}.\)
Trả lời câu hỏi Vận dụng 1 trang 47 SGK Toán 12 Chân trời sáng tạo
Một mô hình cầu treo được thiết kế trong không gian \(Oxyz\) như hình dưới đây. Viết phương trình tham số của làn đường \(d\) đi qua hai điểm \(M\left( {4;3;20} \right)\) và \(N\left( {4;1000;20} \right).\)
Phương pháp giải:
Đường thẳng \(d\) đi qua hai điểm \(M\) và \(N\) nên \(\overrightarrow {MN} \) là một vectơ chỉ phương của đường thẳng, từ đó viết được phương trình tham số của \(d.\)
Lời giải chi tiết:
Ta có \(\overrightarrow {MN} = \left( {0;997;0} \right)\).
Đường thẳng \(d\) đi qua hai điểm \(M\) và \(N\) nên \(\overrightarrow {MN} \) là một vectơ chỉ phương của đường thẳng. Suy ra vectơ \(\vec u = \frac{1}{{997}}\overrightarrow {MN} = \left( {0;1;0} \right)\) cũng là một vectơ chỉ phương của đường thẳng \(d.\)
Phương trình tham số của làn đường \(d\) đi qua \(M\left( {4;3;20} \right)\) và có một vectơ chỉ phương \(\vec u = \left( {0;1;0} \right)\) là \(\left\{ \begin{array}{l}x = 4 + 0t\\y = 3 + t\\z = 20 + 0t\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = 4\\y = 3 + t\\z = 20\end{array} \right.\).
Đặt \(t' = t + 3\), phương trình tham số của làn đường \(d\) là \(\left\{ \begin{array}{l}x = 4\\y = t'\\z = 20\end{array} \right.\).
Mục 1 của SGK Toán 12 tập 2 chương trình Chân trời sáng tạo thường tập trung vào một chủ đề quan trọng trong chương trình học. Việc nắm vững kiến thức và kỹ năng giải bài tập trong mục này là nền tảng để hiểu sâu hơn các kiến thức tiếp theo. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trong mục 1, trang 44, 45, 46, 47, giúp các em học sinh hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Bài 1 thường là bài tập kiểm tra kiến thức cơ bản về lý thuyết. Lời giải sẽ đi kèm với giải thích chi tiết từng bước, giúp các em hiểu rõ tại sao lại chọn phương pháp giải đó và kết quả cuối cùng là gì.
Bài 2 có thể là bài tập áp dụng lý thuyết vào thực tế, đòi hỏi các em phải vận dụng kiến thức đã học để giải quyết vấn đề. Lời giải sẽ tập trung vào việc phân tích đề bài, xác định các yếu tố quan trọng và lựa chọn phương pháp giải phù hợp.
Bài 3 thường là bài tập nâng cao, đòi hỏi các em phải có khả năng tư duy logic và sáng tạo. Lời giải sẽ cung cấp các gợi ý và hướng dẫn chi tiết, giúp các em tự tìm ra lời giải đúng.
Bài 4 có thể là bài tập tổng hợp, kết hợp nhiều kiến thức và kỹ năng khác nhau. Lời giải sẽ giúp các em ôn lại kiến thức đã học và rèn luyện khả năng giải quyết vấn đề phức tạp.
Để giải bài tập Toán 12 hiệu quả, các em cần:
Kiến thức và kỹ năng giải bài tập trong mục 1 trang 44, 45, 46, 47 SGK Toán 12 tập 2 có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, như:
Để học Toán 12 hiệu quả, các em nên:
Hy vọng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải bài tập mục 1 trang 44, 45, 46, 47 SGK Toán 12 tập 2 chương trình Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao trong các kỳ thi sắp tới!