Chào mừng các em học sinh đến với lời giải chi tiết bài tập 3 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập hiệu quả, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập 3 trang 37 thuộc chương trình học Toán 12 tập 1, tập trung vào các kiến thức về giới hạn của hàm số.
Cho hàm số (y = frac{{{x^2} - 4x + 1}}{{x - 4}}). Trong các khẳng định sau, khẳng định nào đúng?
Đề bài
Cho hàm số \(y = \frac{{{x^2} - 4x + 1}}{{x - 4}}\). Trong các khẳng định sau, khẳng định nào đúng?
A. Hàm số đạt cực tiểu tại x = 3, giá trị cực tiểu là y = 2.
B. Hàm số đạt cực tiểu tại x = 5, giá trị cực tiểu là y = 6.
C. Hàm số đạt cực tiểu tại x = 3, giá trị cực tiểu là y = 6.
D. Hàm số đạt cực tiểu tại x = 5, giá trị cực tiểu là y = 2.
Phương pháp giải - Xem chi tiết
Tìm đạo hàm và lập bảng biến thiên
Lời giải chi tiết
Chọn B
\(y' = \frac{{{x^2} - 8x + 15}}{{{{(x - 4)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 5\end{array} \right.\)
Bảng biến thiên:
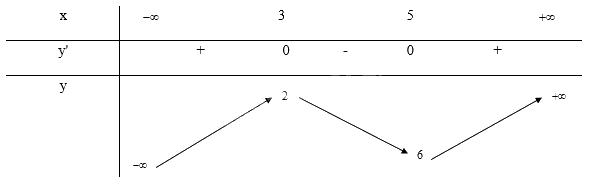
Từ bảng biến thiên ta thấy, hàm số đạt cực đại tại x = 3 và \({y_{cd}} = 2\), đạt cực tiểu tại x = 5 và \({y_{ct}} = 6\)
Bài tập 3 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học về giới hạn của hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về giới hạn, các định lý liên quan và các phương pháp tính giới hạn thường gặp.
Bài tập 3 thường yêu cầu học sinh tính giới hạn của hàm số tại một điểm hoặc khi x tiến tới vô cùng. Các hàm số có thể là hàm đa thức, hàm hữu tỉ, hàm lượng giác hoặc các hàm số khác. Để giải bài tập, học sinh cần xác định đúng dạng của hàm số và áp dụng phương pháp tính giới hạn phù hợp.
Ví dụ: Tính giới hạn \lim_{x \to 2} \frac{x^2 - 4}{x - 2}
Giải:
Vậy, \lim_{x \to 2} \frac{x^2 - 4}{x - 2} = 4
Việc giải bài tập 3 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo không chỉ giúp học sinh hiểu rõ hơn về khái niệm giới hạn mà còn rèn luyện kỹ năng giải toán và tư duy logic. Đây là nền tảng quan trọng để học sinh tiếp thu các kiến thức nâng cao hơn trong chương trình Toán 12 và chuẩn bị cho kỳ thi tốt nghiệp THPT.
Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh có thể tự tin giải bài tập 3 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo một cách hiệu quả. Chúc các em học tập tốt!