Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác các bài tập Toán 12 tập 2 theo chương trình Chân trời sáng tạo. Chúng tôi hiểu rằng việc tự học Toán đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Với mục tiêu hỗ trợ học sinh học tập hiệu quả, chúng tôi đã biên soạn và trình bày lời giải mục 2 trang 24, 25, 26 SGK Toán 12 tập 2 một cách dễ hiểu nhất.
Tính thể tích hình khối
Trả lời câu hỏi Thực hành 5 trang 25 SGK Toán 12 Chân trời sáng tạo
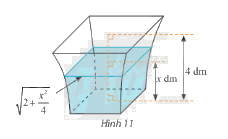
Một bình chứa nước có dạng như hình 11. Biết rằng khi nước ở trong bình có chiều cao \(x\) (dm) \(\left( {0 \le x \le 4} \right)\) thì mặt nước là hình vuông có cạnh \(\sqrt {2 + \frac{{{x^2}}}{4}} \) (dm). Tính dung tích của bình.
Phương pháp giải:
Chọn trục \(Ox\) vuông góc với mặt đáy của bình sao cho đáy nhỏ, đáy to của bình vuông góc với \(Ox\) lần lượt tại \(x = 0\) và \(x = 4\)
Diện tích mặt nước ở chiều cao \(x\) là \(S\left( x \right) = {\left( {\sqrt {2 + \frac{{{x^2}}}{4}} } \right)^2} = 2 + \frac{{{x^2}}}{4}\)
Dung tích của bình là \(V = \int\limits_0^4 {S\left( x \right)dx} \)
Lời giải chi tiết:
Chọn trục \(Ox\) vuông góc với mặt đáy của bình sao cho đáy nhỏ, đáy to của bình vuông góc với \(Ox\) lần lượt tại \(x = 0\) và \(x = 4\)
Diện tích mặt nước ở chiều cao \(x\) là \(S\left( x \right) = {\left( {\sqrt {2 + \frac{{{x^2}}}{4}} } \right)^2} = 2 + \frac{{{x^2}}}{4}\)
Dung tích của bình là \(V = \int\limits_0^4 {S\left( x \right)dx} = \int\limits_0^4 {\left( {2 + \frac{{{x^2}}}{4}} \right)dx} = \left. {\left( {2x + \frac{{{x^3}}}{{12}}} \right)} \right|_0^4 = \frac{{40}}{3}\)
Trả lời câu hỏi Thực hành 6 trang 26 SGK Toán 12 Chân trời sáng tạo
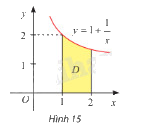
Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = 1 + \frac{1}{x}\), trục hoành và hai đường thẳng \(x = 1\), \(x = 2\) (hình 15). Tính thể tích khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\).
Phương pháp giải:
Thể tích khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\), với \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a\), \(x = b\), là: \(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \)
Lời giải chi tiết:
Thể tích khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\) là:
\(V = \pi \int\limits_1^2 {{{\left( {1 + \frac{1}{x}} \right)}^2}dx} = \pi \int\limits_1^2 {\left( {1 + \frac{2}{x} + \frac{1}{{{x^2}}}} \right)dx} = \pi \left. {\left( {x + 2\ln \left| x \right| - \frac{1}{x}} \right)} \right|_1^2 = \pi \left( {\frac{3}{2} + 2\ln 2} \right)\)
Trả lời câu hỏi Khám phá 3 trang 24 SGK Toán 12 Chân trời sáng tạo
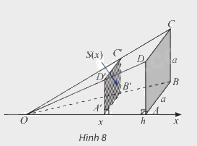
Trong không gian, cho hình chóp \(O.ABCD\) có đáy là hình vuông cạnh \(a\), \(OA \bot \left( {ABCD} \right)\), \(OA = h\). Đặt trục số \(Ox\) như hình 8. Một mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \(\left( {0 < x \le h} \right)\), cắt hình chóp \(O.ABCD\) theo mặt cắt là hình vuông \(A'B'C'D'\). Kí hiệu \(S\left( x \right)\) là diện tích của hình vuông \(A'B'C'D'\).
a) Tính \(S\left( x \right)\) theo \(a\), \(h\) và \(x\).
b) Tính \(\int\limits_0^h {S\left( x \right)dx} \) và so sánh với thể tích của khối chóp \(O.ABCD\).
Phương pháp giải:
a) Do \(A'B'C'D'\) là hình vuông, nên \(S\left( x \right) = A'D{'^2}\)
Tam giác \(OAD\) có \(AD\parallel A'D'\) nên \(\frac{{OA'}}{{OA}} = \frac{{A'D'}}{{AD}}\), từ đó tính được \(A'D'\), sau đó tính \(S\left( x \right)\).
b) Tính \(\int\limits_0^h {S\left( x \right)dx} \) và thể tích khối chóp \(O.ABCD\) và so sánh các kết quả với nhau.
Lời giải chi tiết:
a) Do \(A'B'C'D'\) là hình vuông, nên \(S\left( x \right) = A'D{'^2}\)
Tam giác \(OAD\) có \(AD\parallel A'D'\) nên \(\frac{{OA'}}{{OA}} = \frac{{A'D'}}{{AD}} \Rightarrow A'D' = \frac{{OA'.AD}}{{OA}} = \frac{{x.a}}{h}\)
Suy ra \(S\left( x \right) = A'D{'^2} = {\left( {\frac{{x.a}}{h}} \right)^2} = \frac{{{a^2}}}{{{h^2}}}{x^2}\)
b) Ta có: \(\int\limits_0^h {S\left( x \right)dx} = \frac{{{a^2}}}{{{h^2}}}\int\limits_0^h {{x^2}dx} = \frac{{{a^2}}}{{{h^2}}}\left. {\left( {\frac{{{x^3}}}{3}} \right)} \right|_0^h = \frac{{{a^2}}}{{{h^2}}}.\frac{{{h^3}}}{3} = \frac{{{a^2}h}}{3}\)
Thể tích khối chóp \(O.ABCD\) là \({V_{O.ABCD}} = \frac{1}{3}.{a^2}.h = \frac{{{a^2}h}}{3}\)
Như vậy \({V_{O.ABCD}} = \int\limits_0^h {S\left( x \right)dx} \)
Trả lời câu hỏi Khám phá 4 trang 25 SGK Toán 12 Chân trời sáng tạo
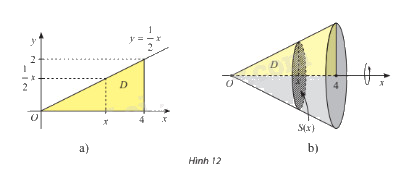
Cho \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right) = \frac{1}{2}x\), trục hoành và đường thẳng \(x = 4\) (hình 12a). Quay hình \(D\) xung quanh trục \(Ox\) thì được một khối nón, kí hiệu là \(N\). (hình 12b)
a) Cắt khối \(N\) bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \(\left( {0 \le x \le 4} \right)\) thì mặt cắt là hình gì? Tính diện tích \(S\left( x \right)\) của mặt cắt đó.
b) Sử dụng công thức tính thể tích hình khối, tính thể tích của khối nón \(N\).
Phương pháp giải:
a) Mặt cắt khi cắt khối nón \(N\) bởi mặt phẳng vuông góc với trục \(Ox\) là hình tròn. Tính bán kính của hình tròn, từ đó tính được diện tích \(S\left( x \right)\) của mặt cắt đó.
b) Công thức tính thể tích của khối nón \(N\) có bán kính đáy \(r\) và chiều cao \(h\): \(V = \frac{1}{3}\pi {r^2}h\).
Lời giải chi tiết:
a) Mặt cắt khi cắt khối nón \(N\) bởi mặt phẳng vuông góc với trục \(Ox\) là hình tròn. Ta nhận thấy rằng khi cắt khối nón \(N\) bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) thì bán kính mặt cắt sẽ là \(\frac{1}{2}x\).
Do đó diện tích của mặt cắt là \(S\left( x \right) = \pi .{\left( {\frac{1}{2}x} \right)^2} = \frac{\pi }{2}{x^2}\).
b) Khối nón \(N\) có bán kính đáy \(r = 2\) và chiều cao \(h = 4\) nên thể tích của khối nón là: \(V = \frac{1}{3}\pi {.2^2}.4 = \frac{{16\pi }}{3}\)
Trả lời câu hỏi Vận dụng 2trang 27 SGK Toán 12 Chân trời sáng tạo
Sử dụng tích phân, tính thể tích khối nón có bán kính đáy \(r\) và chiều cao \(h\). (hình 16)
Phương pháp giải:
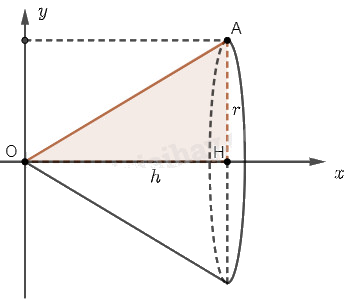
Chọn trục \(Ox\) và \(Oy\) như hình vẽ.
Khi quay hình phẳng \(D\) giới hạn bởi tam giác \(OAH\) quanh trục \(Ox\), ta sẽ được một khối nón có bán kính đáy \(r\) và chiều cao \(h\).
Hình phẳng \(D\) được giới hạn bởi đường thẳng \(OA\) có phương trình \(y = f\left( x \right) = ax + b\), trục hoành và hai đường thẳng \(x = 0\), \(x = h\).
Thể tích của khối nón là \(V = \pi \int\limits_0^h {{f^2}\left( x \right)dx} \)
Lời giải chi tiết:
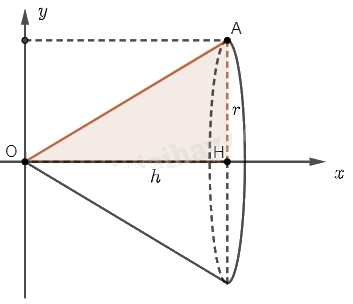
Chọn trục \(Ox\) và \(Oy\) như hình vẽ.
Khi quay hình phẳng \(D\) giới hạn bởi tam giác \(OAH\) quanh trục \(Ox\), ta sẽ được một khối nón có bán kính đáy \(r\) và chiều cao \(h\).
Hình phẳng \(D\) được giới hạn bởi đường thẳng \(OA\) có phương trình \(y = f\left( x \right) = ax + b\), trục hoành và hai đường thẳng \(x = 0\), \(x = h\).
Đường thẳng \(OA\) đi qua điểm \(O\left( {0;0} \right)\) và \(A\left( {h;r} \right)\) nên phương trình đường thẳng \(OA\) là \(y = \frac{r}{h}x\).
Thể tích khối nón là:
\(V = \pi \int\limits_0^h {{{\left( {\frac{r}{h}x} \right)}^2}dx} = \pi \frac{{{r^2}}}{{{h^2}}}\int\limits_0^h {{x^2}dx} = \frac{{\pi {r^2}}}{{{h^2}}}.\left. {\left( {\frac{{{x^3}}}{3}} \right)} \right|_0^h = \frac{{\pi {r^2}}}{{{h^2}}}.\frac{{{h^3}}}{3} = \frac{{\pi {r^2}h}}{3}\)
Trả lời câu hỏi Khám phá 3 trang 24 SGK Toán 12 Chân trời sáng tạo
Trong không gian, cho hình chóp \(O.ABCD\) có đáy là hình vuông cạnh \(a\), \(OA \bot \left( {ABCD} \right)\), \(OA = h\). Đặt trục số \(Ox\) như hình 8. Một mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \(\left( {0 < x \le h} \right)\), cắt hình chóp \(O.ABCD\) theo mặt cắt là hình vuông \(A'B'C'D'\). Kí hiệu \(S\left( x \right)\) là diện tích của hình vuông \(A'B'C'D'\).
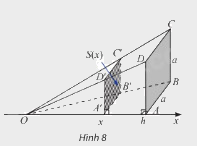
a) Tính \(S\left( x \right)\) theo \(a\), \(h\) và \(x\).
b) Tính \(\int\limits_0^h {S\left( x \right)dx} \) và so sánh với thể tích của khối chóp \(O.ABCD\).
Phương pháp giải:
a) Do \(A'B'C'D'\) là hình vuông, nên \(S\left( x \right) = A'D{'^2}\)
Tam giác \(OAD\) có \(AD\parallel A'D'\) nên \(\frac{{OA'}}{{OA}} = \frac{{A'D'}}{{AD}}\), từ đó tính được \(A'D'\), sau đó tính \(S\left( x \right)\).
b) Tính \(\int\limits_0^h {S\left( x \right)dx} \) và thể tích khối chóp \(O.ABCD\) và so sánh các kết quả với nhau.
Lời giải chi tiết:
a) Do \(A'B'C'D'\) là hình vuông, nên \(S\left( x \right) = A'D{'^2}\)
Tam giác \(OAD\) có \(AD\parallel A'D'\) nên \(\frac{{OA'}}{{OA}} = \frac{{A'D'}}{{AD}} \Rightarrow A'D' = \frac{{OA'.AD}}{{OA}} = \frac{{x.a}}{h}\)
Suy ra \(S\left( x \right) = A'D{'^2} = {\left( {\frac{{x.a}}{h}} \right)^2} = \frac{{{a^2}}}{{{h^2}}}{x^2}\)
b) Ta có: \(\int\limits_0^h {S\left( x \right)dx} = \frac{{{a^2}}}{{{h^2}}}\int\limits_0^h {{x^2}dx} = \frac{{{a^2}}}{{{h^2}}}\left. {\left( {\frac{{{x^3}}}{3}} \right)} \right|_0^h = \frac{{{a^2}}}{{{h^2}}}.\frac{{{h^3}}}{3} = \frac{{{a^2}h}}{3}\)
Thể tích khối chóp \(O.ABCD\) là \({V_{O.ABCD}} = \frac{1}{3}.{a^2}.h = \frac{{{a^2}h}}{3}\)
Như vậy \({V_{O.ABCD}} = \int\limits_0^h {S\left( x \right)dx} \)
Trả lời câu hỏi Thực hành 5 trang 25 SGK Toán 12 Chân trời sáng tạo
Một bình chứa nước có dạng như hình 11. Biết rằng khi nước ở trong bình có chiều cao \(x\) (dm) \(\left( {0 \le x \le 4} \right)\) thì mặt nước là hình vuông có cạnh \(\sqrt {2 + \frac{{{x^2}}}{4}} \) (dm). Tính dung tích của bình.
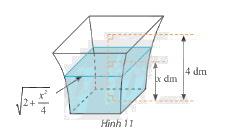
Phương pháp giải:
Chọn trục \(Ox\) vuông góc với mặt đáy của bình sao cho đáy nhỏ, đáy to của bình vuông góc với \(Ox\) lần lượt tại \(x = 0\) và \(x = 4\)
Diện tích mặt nước ở chiều cao \(x\) là \(S\left( x \right) = {\left( {\sqrt {2 + \frac{{{x^2}}}{4}} } \right)^2} = 2 + \frac{{{x^2}}}{4}\)
Dung tích của bình là \(V = \int\limits_0^4 {S\left( x \right)dx} \)
Lời giải chi tiết:
Chọn trục \(Ox\) vuông góc với mặt đáy của bình sao cho đáy nhỏ, đáy to của bình vuông góc với \(Ox\) lần lượt tại \(x = 0\) và \(x = 4\)
Diện tích mặt nước ở chiều cao \(x\) là \(S\left( x \right) = {\left( {\sqrt {2 + \frac{{{x^2}}}{4}} } \right)^2} = 2 + \frac{{{x^2}}}{4}\)
Dung tích của bình là \(V = \int\limits_0^4 {S\left( x \right)dx} = \int\limits_0^4 {\left( {2 + \frac{{{x^2}}}{4}} \right)dx} = \left. {\left( {2x + \frac{{{x^3}}}{{12}}} \right)} \right|_0^4 = \frac{{40}}{3}\)
Trả lời câu hỏi Khám phá 4 trang 25 SGK Toán 12 Chân trời sáng tạo
Cho \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right) = \frac{1}{2}x\), trục hoành và đường thẳng \(x = 4\) (hình 12a). Quay hình \(D\) xung quanh trục \(Ox\) thì được một khối nón, kí hiệu là \(N\). (hình 12b)
a) Cắt khối \(N\) bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \(\left( {0 \le x \le 4} \right)\) thì mặt cắt là hình gì? Tính diện tích \(S\left( x \right)\) của mặt cắt đó.
b) Sử dụng công thức tính thể tích hình khối, tính thể tích của khối nón \(N\).
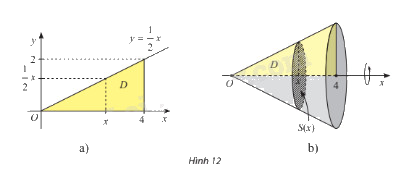
Phương pháp giải:
a) Mặt cắt khi cắt khối nón \(N\) bởi mặt phẳng vuông góc với trục \(Ox\) là hình tròn. Tính bán kính của hình tròn, từ đó tính được diện tích \(S\left( x \right)\) của mặt cắt đó.
b) Công thức tính thể tích của khối nón \(N\) có bán kính đáy \(r\) và chiều cao \(h\): \(V = \frac{1}{3}\pi {r^2}h\).
Lời giải chi tiết:
a) Mặt cắt khi cắt khối nón \(N\) bởi mặt phẳng vuông góc với trục \(Ox\) là hình tròn. Ta nhận thấy rằng khi cắt khối nón \(N\) bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) thì bán kính mặt cắt sẽ là \(\frac{1}{2}x\).
Do đó diện tích của mặt cắt là \(S\left( x \right) = \pi .{\left( {\frac{1}{2}x} \right)^2} = \frac{\pi }{2}{x^2}\).
b) Khối nón \(N\) có bán kính đáy \(r = 2\) và chiều cao \(h = 4\) nên thể tích của khối nón là: \(V = \frac{1}{3}\pi {.2^2}.4 = \frac{{16\pi }}{3}\)
Trả lời câu hỏi Thực hành 6 trang 26 SGK Toán 12 Chân trời sáng tạo
Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = 1 + \frac{1}{x}\), trục hoành và hai đường thẳng \(x = 1\), \(x = 2\) (hình 15). Tính thể tích khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\).
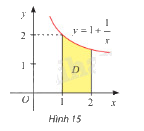
Phương pháp giải:
Thể tích khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\), với \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a\), \(x = b\), là: \(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \)
Lời giải chi tiết:
Thể tích khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\) là:
\(V = \pi \int\limits_1^2 {{{\left( {1 + \frac{1}{x}} \right)}^2}dx} = \pi \int\limits_1^2 {\left( {1 + \frac{2}{x} + \frac{1}{{{x^2}}}} \right)dx} = \pi \left. {\left( {x + 2\ln \left| x \right| - \frac{1}{x}} \right)} \right|_1^2 = \pi \left( {\frac{3}{2} + 2\ln 2} \right)\)
Trả lời câu hỏi Vận dụng 2trang 27 SGK Toán 12 Chân trời sáng tạo
Sử dụng tích phân, tính thể tích khối nón có bán kính đáy \(r\) và chiều cao \(h\). (hình 16)
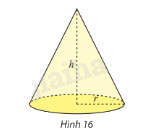
Phương pháp giải:
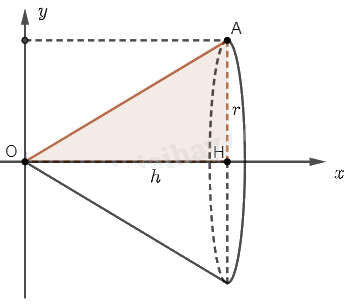
Chọn trục \(Ox\) và \(Oy\) như hình vẽ.
Khi quay hình phẳng \(D\) giới hạn bởi tam giác \(OAH\) quanh trục \(Ox\), ta sẽ được một khối nón có bán kính đáy \(r\) và chiều cao \(h\).
Hình phẳng \(D\) được giới hạn bởi đường thẳng \(OA\) có phương trình \(y = f\left( x \right) = ax + b\), trục hoành và hai đường thẳng \(x = 0\), \(x = h\).
Thể tích của khối nón là \(V = \pi \int\limits_0^h {{f^2}\left( x \right)dx} \)
Lời giải chi tiết:
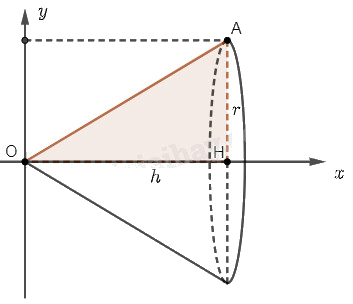
Chọn trục \(Ox\) và \(Oy\) như hình vẽ.
Khi quay hình phẳng \(D\) giới hạn bởi tam giác \(OAH\) quanh trục \(Ox\), ta sẽ được một khối nón có bán kính đáy \(r\) và chiều cao \(h\).
Hình phẳng \(D\) được giới hạn bởi đường thẳng \(OA\) có phương trình \(y = f\left( x \right) = ax + b\), trục hoành và hai đường thẳng \(x = 0\), \(x = h\).
Đường thẳng \(OA\) đi qua điểm \(O\left( {0;0} \right)\) và \(A\left( {h;r} \right)\) nên phương trình đường thẳng \(OA\) là \(y = \frac{r}{h}x\).
Thể tích khối nón là:
\(V = \pi \int\limits_0^h {{{\left( {\frac{r}{h}x} \right)}^2}dx} = \pi \frac{{{r^2}}}{{{h^2}}}\int\limits_0^h {{x^2}dx} = \frac{{\pi {r^2}}}{{{h^2}}}.\left. {\left( {\frac{{{x^3}}}{3}} \right)} \right|_0^h = \frac{{\pi {r^2}}}{{{h^2}}}.\frac{{{h^3}}}{3} = \frac{{\pi {r^2}h}}{3}\)
Mục 2 trong SGK Toán 12 tập 2 Chân trời sáng tạo thường tập trung vào một chủ đề quan trọng trong chương trình, đòi hỏi học sinh phải nắm vững lý thuyết và kỹ năng giải bài tập. Việc giải đúng và hiểu rõ các bài tập trong mục này là nền tảng để học tốt các kiến thức tiếp theo.
Để hiểu rõ hơn về Mục 2, chúng ta cần xác định nội dung chính mà nó đề cập đến. Thông thường, đây có thể là một dạng toán cụ thể, một định lý mới, hoặc một phương pháp giải toán đặc biệt. Việc nắm bắt được nội dung chính sẽ giúp học sinh tập trung vào những kiến thức quan trọng nhất.
Bài 1: (Nêu lại đề bài). Lời giải: ... (Giải chi tiết từng bước).
Bài 2: (Nêu lại đề bài). Lời giải: ... (Giải chi tiết từng bước).
Bài 3: (Nêu lại đề bài). Lời giải: ... (Giải chi tiết từng bước).
Bài 4: (Nêu lại đề bài). Lời giải: ... (Giải chi tiết từng bước).
Bài 5: (Nêu lại đề bài). Lời giải: ... (Giải chi tiết từng bước).
Bài 6: (Nêu lại đề bài). Lời giải: ... (Giải chi tiết từng bước).
Trong quá trình giải bài tập, hãy chú ý đến các dấu hiệu quan trọng, các điều kiện ràng buộc, và các trường hợp đặc biệt. Việc phân tích kỹ đề bài và lựa chọn phương pháp giải phù hợp là yếu tố then chốt để đạt được kết quả tốt nhất.
Kiến thức và kỹ năng thu được từ việc giải Mục 2 trang 24, 25, 26 SGK Toán 12 tập 2 Chân trời sáng tạo có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau của Toán học, cũng như trong thực tế cuộc sống. Việc nắm vững kiến thức này sẽ giúp bạn tự tin hơn khi giải quyết các bài toán phức tạp và ứng dụng Toán học vào các tình huống thực tế.
Để nâng cao kiến thức và kỹ năng giải Toán 12, bạn có thể tham khảo thêm các tài liệu sau:
Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!