Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 61, 62, 63 sách giáo khoa Toán 12 tập 2 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn học Toán.
Trong không gian (Oxyz), cho mặt cầu (Sleft( {I;R} right)) có tâm (Ileft( {a;b;c} right)) và bán kính (R). Xét một điểm (Mleft( {x;y;z} right)) thay đổi. a) Tính khoảng cách (IM) theo (x), (y), (z) và (a), (b), (c). b) Nêu điều kiện cần và đủ của (x), (y), (z) để điểm (Mleft( {x;y;z} right)) nằm trên mặt cầu (Sleft( {I;R} right)).
Trả lời câu hỏi Thực hành 1 trang 62 SGK Toán 12 Chân trời sáng tạo
Viết phương trình mặt cầu \(\left( S \right)\):
a) Có tâm \(I\left( {3; - 2; - 4} \right)\), bán kính \(R = 10\).
b) Có đường kính \(EF\) với \(E\left( {3; - 1;8} \right)\) và \(F\left( {7; - 3;0} \right)\).
c) Có tâm \(M\left( { - 2;1;3} \right)\) và đi qua điểm \(N\left( {2; - 3; - 4} \right)\).
Phương pháp giải:
a) Mặt cầu \(\left( S \right)\) tâm \(I\left( {a;b;c} \right)\) và bán kính \(R\) có phương trình là
\({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\)
b) Mặt cầu \(\left( S \right)\) có đường kính \(EF\), suy ra \(\left( S \right)\) có tâm \(I\) là trung điểm của \(EF\) và bán kính bằng \(\frac{{EF}}{2}\), từ đó viết phương trình mặt cầu \(\left( S \right)\) theo như câu a.
c) Mặt cầu \(\left( S \right)\) có tâm \(M\) và đi qua \(N\), nên \(MN\) là một bán kính của \(\left( S \right)\), từ đó viết phương trình mặt cầu \(\left( S \right)\) theo như câu a.
Lời giải chi tiết:
a) Mặt cầu \(\left( S \right)\) tâm \(I\left( {3; - 2; - 4} \right)\), bán kính \(R = 10\) có phương trình là
\({\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z + 4} \right)^2} = 100\).
b) Mặt cầu \(\left( S \right)\) có đường kính \(EF\), suy ra \(\left( S \right)\) có tâm \(I\) là trung điểm của \(EF\) và bán kính bằng \(\frac{{EF}}{2}\).
Ta có \(E\left( {3; - 1;8} \right)\) và \(F\left( {7; - 3;0} \right)\), suy ra \(I\left( {5; - 2;4} \right)\).
Ta có \(EF = \sqrt {{{\left( {3 - 7} \right)}^2} + {{\left( { - 1 + 3} \right)}^2} + {{\left( {8 - 0} \right)}^2}} = 2\sqrt {21} \), suy ra \(R = \frac{{EF}}{2} = \sqrt {21} \).
Vậy phương trình mặt cầu \(\left( S \right)\) là \({\left( {x - 5} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 4} \right)^2} = 21\).
c) Mặt cầu \(\left( S \right)\) có tâm \(M\) và đi qua \(N\), nên \(MN\) là một bán kính của \(\left( S \right)\).
Ta có \(MN = \sqrt {{{\left( { - 2 - 2} \right)}^2} + {{\left( {1 + 3} \right)}^2} + {{\left( {3 + 4} \right)}^2}} = 9\).
Vậy phương trình mặt cầu \(\left( S \right)\) là \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 3} \right)^2} = 81\).
Trả lời câu hỏi Hoạt động 2 trang 63 SGK Toán 12 Chân trời sáng tạo
a) Trong không gian \(Oxyz\), cho điểm \(M\left( {x;y;z} \right)\) thay đổi có toạ độ luôn thoả mãn phương trình \({x^2} + {y^2} + {z^2} - 2x - 4y - 6z - 11 = 0\). (*)
i) Biến đổi (*) về dạng \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 25\).
ii) Chứng tỏ \(M\left( {x;y;z} \right)\) luôn thuộc một mặt cầu \(\left( S \right)\). Tìm tâm và bán kính của \(\left( S \right)\)
b) Bằng cách biến đổi phương trình \({x^2} + {y^2} + {z^2} - 2x - 4y - 6z + 15 = 0\) (**) về dạng \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = - 1\), hãy cho biết phương trình (**) có thể là phương trình mặt cầu hay không.
Phương pháp giải:
a) Sử dụng các hằng đẳng thức để đưa phương trình (*) về dạng như đề bài yêu cầu, từ đó suy ra điểm \(M\) luôn thuộc mặt cầu \(\left( S \right)\).
b) Sử dụng hằng đẳng thức để đưa phương trình (**) về dạng như đề bài yêu cầu, rồi kết luận.
Lời giải chi tiết:
a)
i) Ta có
\(\begin{array}{l}{x^2} + {y^2} + {z^2} - 2x - 4y - 6z - 11 = 0\\ \Leftrightarrow \left( {{x^2} - 2x + 1} \right) + \left( {{y^2} - 4y + 4} \right) + \left( {{z^2} - 6z + 9} \right) - 25 = 0\\ \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 25\end{array}.\)
ii) Do điểm \(M\left( {x;y;z} \right)\) có toạ độ thoả mãn phương trình (*), suy ra điểm \(M\) thoả mãn phương trình \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 25\). Vậy điểm \(M\) thuộc mặt cầu \(\left( S \right)\) có tâm \(I\left( {1;2;3} \right)\) và bán kính \(R = \sqrt {25} = 5\).
b) Ta có
\(\begin{array}{l}{x^2} + {y^2} + {z^2} - 2x - 4y - 6z + 15 = 0\\ \Leftrightarrow \left( {{x^2} - 2x + 1} \right) + \left( {{y^2} - 4y + 4} \right) + \left( {{z^2} - 6z + 9} \right) + 1 = 0\\ \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = - 1\end{array}.\)
Do \( - 1 < 0\), nên phương trình trên không là phương trình mặt cầu. Suy ra (**) không là phương trình mặt cầu.
Trả lời câu hỏi Thực hành 2 trang 63 SGK Toán 12 Chân trời sáng tạo
Trong các phương trình sau, phương trình nào là phương trình mặt cầu? Xác định tâm và bán kính của mặt cầu đó.
a) \({x^2} + {y^2} + {z^2} + 4z - 32 = 0\)
b) \({x^2} + {y^2} + {z^2} + 2x + 2y - 2z + 4 = 0\)
Phương pháp giải:
Các phương trình ở câu a và b đều là phương trình mặt cầu có dạng \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\). Xác định \(a\), \(b\), \(c\), \(d\) và tính \({a^2} + {b^2} + {c^2} - d\), rồi rút ra kết luận.
Lời giải chi tiết:
Các phương trình ở câu a và b đều là phương trình mặt cầu có dạng \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\).
a) Với phương trình \({x^2} + {y^2} + {z^2} + 4z - 32 = 0\), ta có \(a = 0\), \(b = 0\), \(c = - 2\) và \(d = - 32\).
Ta có \({a^2} + {b^2} + {c^2} - d = {0^2} + {0^2} + {\left( { - 2} \right)^2} + 32 = 36 > 0\).
Vậy phương trình \({x^2} + {y^2} + {z^2} + 4z - 32 = 0\) là phương trình mặt cầu tâm \(I\left( {0;0; - 2} \right)\) và bán kính \(R = 6\).
b) Với phương trình \({x^2} + {y^2} + {z^2} + 2x + 2y - 2z + 4 = 0\), ta có \(a = - 1\), \(b = - 1\), \(c = 1\) và \(d = 4\).
Ta có \({a^2} + {b^2} + {c^2} - d = {\left( { - 1} \right)^2} + {\left( { - 1} \right)^2} + {1^2} - 4 = - 1 < 0.\)
Vậy phương trình \({x^2} + {y^2} + {z^2} + 2x + 2y - 2z + 4 = 0\) không là phương trình mặt cầu.
Trả lời câu hỏi Vận dụng 1 trang 62 SGK Toán 12 Chân trời sáng tạo
Trong không gian \(Oxyz\) (đơn vị của các trục toạ độ là mét), các nhà nghiên cứu khí tượng dùng một phần mềm mô phỏng bề mặt của một quả bóng thám không có dạng hình cầu bằng phương trình \({\left( {x - 300} \right)^2} + {\left( {y - 400} \right)^2} + {\left( {z - 2000} \right)^2} = 1\). Tìm toạ độ tâm, bán kính của quả bóng và tính khoảng cách từ tâm của quả bóng đến mặt đất có phương trình \(z = 0\).

Phương pháp giải:
Từ phương trình mặt cầu, chỉ ra tâm và bán kính của quả bóng thám không. Sau đó sử dụng công thức tính khoảng cách từ một điểm đến một mặt phẳng để tính khoảng cách từ tâm của quả bóng đến mặt đất.
Lời giải chi tiết:
Phương trình bề mặt của quả bóng thám không là \({\left( {x - 300} \right)^2} + {\left( {y - 400} \right)^2} + {\left( {z - 2000} \right)^2} = 1\), suy ra quả bóng có tâm \(I\left( {300;400;2000} \right)\) và bán kính \(R = 1.\)
Khoảng cách từ tâm quả bóng đến mặt đất là
\(d = \frac{{\left| {0.300 + 0.400 + 1.2000 + 0} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} }} = 2000\) (mét).
Trả lời câu hỏi Hoạt động 1 trang 61 SGK Toán 12 Chân trời sáng tạo
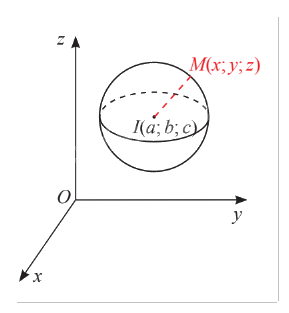
Trong không gian \(Oxyz\), cho mặt cầu \(S\left( {I;R} \right)\) có tâm \(I\left( {a;b;c} \right)\) và bán kính \(R\). Xét một điểm \(M\left( {x;y;z} \right)\) thay đổi.
a) Tính khoảng cách \(IM\) theo \(x\), \(y\), \(z\) và \(a\), \(b\), \(c\).
b) Nêu điều kiện cần và đủ của \(x\), \(y\), \(z\) để điểm \(M\left( {x;y;z} \right)\) nằm trên mặt cầu \(S\left( {I;R} \right)\).
Phương pháp giải:
a) Sử dụng công thức tính khoảng cách giữa hai điểm trong không gian để tính khoảng cách \(IM\).
b) Để điểm \(M\) nằm trên mặt cầu \(S\left( {I;R} \right)\) thì \(IM = R\).
Lời giải chi tiết:
a) Ta có \(I\left( {a;b;c} \right)\) và \(M\left( {x;y;z} \right)\). Suy ra \(IM = \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} \).
b) Điều kiện cần và đủ của \(x\), \(y\), \(z\) để điểm \(M\left( {x;y;z} \right)\) nằm trên mặt cầu \(S\left( {I;R} \right)\) là \(IM = R\), điều này tương đương với
\(\sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} = R \Leftrightarrow {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).
Trả lời câu hỏi Hoạt động 1 trang 61 SGK Toán 12 Chân trời sáng tạo
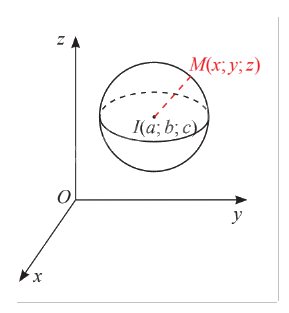
Trong không gian \(Oxyz\), cho mặt cầu \(S\left( {I;R} \right)\) có tâm \(I\left( {a;b;c} \right)\) và bán kính \(R\). Xét một điểm \(M\left( {x;y;z} \right)\) thay đổi.
a) Tính khoảng cách \(IM\) theo \(x\), \(y\), \(z\) và \(a\), \(b\), \(c\).
b) Nêu điều kiện cần và đủ của \(x\), \(y\), \(z\) để điểm \(M\left( {x;y;z} \right)\) nằm trên mặt cầu \(S\left( {I;R} \right)\).
Phương pháp giải:
a) Sử dụng công thức tính khoảng cách giữa hai điểm trong không gian để tính khoảng cách \(IM\).
b) Để điểm \(M\) nằm trên mặt cầu \(S\left( {I;R} \right)\) thì \(IM = R\).
Lời giải chi tiết:
a) Ta có \(I\left( {a;b;c} \right)\) và \(M\left( {x;y;z} \right)\). Suy ra \(IM = \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} \).
b) Điều kiện cần và đủ của \(x\), \(y\), \(z\) để điểm \(M\left( {x;y;z} \right)\) nằm trên mặt cầu \(S\left( {I;R} \right)\) là \(IM = R\), điều này tương đương với
\(\sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} = R \Leftrightarrow {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).
Trả lời câu hỏi Thực hành 1 trang 62 SGK Toán 12 Chân trời sáng tạo
Viết phương trình mặt cầu \(\left( S \right)\):
a) Có tâm \(I\left( {3; - 2; - 4} \right)\), bán kính \(R = 10\).
b) Có đường kính \(EF\) với \(E\left( {3; - 1;8} \right)\) và \(F\left( {7; - 3;0} \right)\).
c) Có tâm \(M\left( { - 2;1;3} \right)\) và đi qua điểm \(N\left( {2; - 3; - 4} \right)\).
Phương pháp giải:
a) Mặt cầu \(\left( S \right)\) tâm \(I\left( {a;b;c} \right)\) và bán kính \(R\) có phương trình là
\({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\)
b) Mặt cầu \(\left( S \right)\) có đường kính \(EF\), suy ra \(\left( S \right)\) có tâm \(I\) là trung điểm của \(EF\) và bán kính bằng \(\frac{{EF}}{2}\), từ đó viết phương trình mặt cầu \(\left( S \right)\) theo như câu a.
c) Mặt cầu \(\left( S \right)\) có tâm \(M\) và đi qua \(N\), nên \(MN\) là một bán kính của \(\left( S \right)\), từ đó viết phương trình mặt cầu \(\left( S \right)\) theo như câu a.
Lời giải chi tiết:
a) Mặt cầu \(\left( S \right)\) tâm \(I\left( {3; - 2; - 4} \right)\), bán kính \(R = 10\) có phương trình là
\({\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z + 4} \right)^2} = 100\).
b) Mặt cầu \(\left( S \right)\) có đường kính \(EF\), suy ra \(\left( S \right)\) có tâm \(I\) là trung điểm của \(EF\) và bán kính bằng \(\frac{{EF}}{2}\).
Ta có \(E\left( {3; - 1;8} \right)\) và \(F\left( {7; - 3;0} \right)\), suy ra \(I\left( {5; - 2;4} \right)\).
Ta có \(EF = \sqrt {{{\left( {3 - 7} \right)}^2} + {{\left( { - 1 + 3} \right)}^2} + {{\left( {8 - 0} \right)}^2}} = 2\sqrt {21} \), suy ra \(R = \frac{{EF}}{2} = \sqrt {21} \).
Vậy phương trình mặt cầu \(\left( S \right)\) là \({\left( {x - 5} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 4} \right)^2} = 21\).
c) Mặt cầu \(\left( S \right)\) có tâm \(M\) và đi qua \(N\), nên \(MN\) là một bán kính của \(\left( S \right)\).
Ta có \(MN = \sqrt {{{\left( { - 2 - 2} \right)}^2} + {{\left( {1 + 3} \right)}^2} + {{\left( {3 + 4} \right)}^2}} = 9\).
Vậy phương trình mặt cầu \(\left( S \right)\) là \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 3} \right)^2} = 81\).
Trả lời câu hỏi Vận dụng 1 trang 62 SGK Toán 12 Chân trời sáng tạo
Trong không gian \(Oxyz\) (đơn vị của các trục toạ độ là mét), các nhà nghiên cứu khí tượng dùng một phần mềm mô phỏng bề mặt của một quả bóng thám không có dạng hình cầu bằng phương trình \({\left( {x - 300} \right)^2} + {\left( {y - 400} \right)^2} + {\left( {z - 2000} \right)^2} = 1\). Tìm toạ độ tâm, bán kính của quả bóng và tính khoảng cách từ tâm của quả bóng đến mặt đất có phương trình \(z = 0\).

Phương pháp giải:
Từ phương trình mặt cầu, chỉ ra tâm và bán kính của quả bóng thám không. Sau đó sử dụng công thức tính khoảng cách từ một điểm đến một mặt phẳng để tính khoảng cách từ tâm của quả bóng đến mặt đất.
Lời giải chi tiết:
Phương trình bề mặt của quả bóng thám không là \({\left( {x - 300} \right)^2} + {\left( {y - 400} \right)^2} + {\left( {z - 2000} \right)^2} = 1\), suy ra quả bóng có tâm \(I\left( {300;400;2000} \right)\) và bán kính \(R = 1.\)
Khoảng cách từ tâm quả bóng đến mặt đất là
\(d = \frac{{\left| {0.300 + 0.400 + 1.2000 + 0} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} }} = 2000\) (mét).
Trả lời câu hỏi Hoạt động 2 trang 63 SGK Toán 12 Chân trời sáng tạo
a) Trong không gian \(Oxyz\), cho điểm \(M\left( {x;y;z} \right)\) thay đổi có toạ độ luôn thoả mãn phương trình \({x^2} + {y^2} + {z^2} - 2x - 4y - 6z - 11 = 0\). (*)
i) Biến đổi (*) về dạng \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 25\).
ii) Chứng tỏ \(M\left( {x;y;z} \right)\) luôn thuộc một mặt cầu \(\left( S \right)\). Tìm tâm và bán kính của \(\left( S \right)\)
b) Bằng cách biến đổi phương trình \({x^2} + {y^2} + {z^2} - 2x - 4y - 6z + 15 = 0\) (**) về dạng \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = - 1\), hãy cho biết phương trình (**) có thể là phương trình mặt cầu hay không.
Phương pháp giải:
a) Sử dụng các hằng đẳng thức để đưa phương trình (*) về dạng như đề bài yêu cầu, từ đó suy ra điểm \(M\) luôn thuộc mặt cầu \(\left( S \right)\).
b) Sử dụng hằng đẳng thức để đưa phương trình (**) về dạng như đề bài yêu cầu, rồi kết luận.
Lời giải chi tiết:
a)
i) Ta có
\(\begin{array}{l}{x^2} + {y^2} + {z^2} - 2x - 4y - 6z - 11 = 0\\ \Leftrightarrow \left( {{x^2} - 2x + 1} \right) + \left( {{y^2} - 4y + 4} \right) + \left( {{z^2} - 6z + 9} \right) - 25 = 0\\ \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 25\end{array}.\)
ii) Do điểm \(M\left( {x;y;z} \right)\) có toạ độ thoả mãn phương trình (*), suy ra điểm \(M\) thoả mãn phương trình \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 25\). Vậy điểm \(M\) thuộc mặt cầu \(\left( S \right)\) có tâm \(I\left( {1;2;3} \right)\) và bán kính \(R = \sqrt {25} = 5\).
b) Ta có
\(\begin{array}{l}{x^2} + {y^2} + {z^2} - 2x - 4y - 6z + 15 = 0\\ \Leftrightarrow \left( {{x^2} - 2x + 1} \right) + \left( {{y^2} - 4y + 4} \right) + \left( {{z^2} - 6z + 9} \right) + 1 = 0\\ \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = - 1\end{array}.\)
Do \( - 1 < 0\), nên phương trình trên không là phương trình mặt cầu. Suy ra (**) không là phương trình mặt cầu.
Trả lời câu hỏi Thực hành 2 trang 63 SGK Toán 12 Chân trời sáng tạo
Trong các phương trình sau, phương trình nào là phương trình mặt cầu? Xác định tâm và bán kính của mặt cầu đó.
a) \({x^2} + {y^2} + {z^2} + 4z - 32 = 0\)
b) \({x^2} + {y^2} + {z^2} + 2x + 2y - 2z + 4 = 0\)
Phương pháp giải:
Các phương trình ở câu a và b đều là phương trình mặt cầu có dạng \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\). Xác định \(a\), \(b\), \(c\), \(d\) và tính \({a^2} + {b^2} + {c^2} - d\), rồi rút ra kết luận.
Lời giải chi tiết:
Các phương trình ở câu a và b đều là phương trình mặt cầu có dạng \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\).
a) Với phương trình \({x^2} + {y^2} + {z^2} + 4z - 32 = 0\), ta có \(a = 0\), \(b = 0\), \(c = - 2\) và \(d = - 32\).
Ta có \({a^2} + {b^2} + {c^2} - d = {0^2} + {0^2} + {\left( { - 2} \right)^2} + 32 = 36 > 0\).
Vậy phương trình \({x^2} + {y^2} + {z^2} + 4z - 32 = 0\) là phương trình mặt cầu tâm \(I\left( {0;0; - 2} \right)\) và bán kính \(R = 6\).
b) Với phương trình \({x^2} + {y^2} + {z^2} + 2x + 2y - 2z + 4 = 0\), ta có \(a = - 1\), \(b = - 1\), \(c = 1\) và \(d = 4\).
Ta có \({a^2} + {b^2} + {c^2} - d = {\left( { - 1} \right)^2} + {\left( { - 1} \right)^2} + {1^2} - 4 = - 1 < 0.\)
Vậy phương trình \({x^2} + {y^2} + {z^2} + 2x + 2y - 2z + 4 = 0\) không là phương trình mặt cầu.
Mục 1 của chương trình Toán 12 tập 2 - Chân trời sáng tạo thường tập trung vào một chủ đề quan trọng, ví dụ như đạo hàm của hàm số, ứng dụng đạo hàm để khảo sát hàm số, hoặc tích phân. Việc nắm vững kiến thức và kỹ năng giải bài tập trong mục này là nền tảng để học tốt các kiến thức tiếp theo và làm bài thi hiệu quả.
Để giúp các em hiểu rõ hơn về cách giải các bài tập trong mục này, chúng tôi sẽ trình bày chi tiết lời giải cho từng bài tập trên trang 61, 62 và 63 của SGK Toán 12 tập 2 - Chân trời sáng tạo.
Bài tập 1 thường yêu cầu các em vận dụng kiến thức về đạo hàm để tính đạo hàm của một hàm số cho trước. Để giải bài tập này, các em cần nắm vững các công thức đạo hàm cơ bản và quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số.
Bài tập 2 có thể yêu cầu các em sử dụng đạo hàm để khảo sát hàm số, tìm cực trị, điểm uốn, và vẽ đồ thị hàm số. Để giải bài tập này, các em cần thực hiện các bước sau:
Bài tập 3 có thể liên quan đến ứng dụng đạo hàm để giải các bài toán thực tế, ví dụ như bài toán tối ưu hóa. Để giải bài tập này, các em cần xây dựng hàm số biểu diễn đại lượng cần tối ưu hóa, tìm đạo hàm của hàm số, và giải phương trình đạo hàm bằng 0 để tìm điểm cực trị.
Ngoài SGK Toán 12 tập 2 - Chân trời sáng tạo, các em có thể tham khảo thêm các tài liệu sau để học tốt môn Toán:
Hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể trong bài viết này, các em sẽ tự tin hơn khi giải các bài tập trong mục 1 trang 61, 62, 63 SGK Toán 12 tập 2 - Chân trời sáng tạo. Chúc các em học tốt và đạt kết quả cao trong môn Toán!