Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12 tập 1 - Chân trời sáng tạo. Bài viết này sẽ giúp bạn giải quyết triệt để bài tập 5 trang 51, nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, giúp bạn tiết kiệm thời gian và đạt kết quả cao trong môn Toán.
Cho hình lăng trụ tam giác ABC.A′B′C′ có (overrightarrow {AA'} = overrightarrow a ,overrightarrow {AB} = overrightarrow b ,overrightarrow {AC} = overrightarrow c ). Chứng minh rằng (overrightarrow {B'C} = overrightarrow c - overrightarrow a - overrightarrow b ) và (overrightarrow {BC'} = overrightarrow a - overrightarrow b + overrightarrow c )
Đề bài
Cho hình lăng trụ tam giác ABC.A′B′C′ có \(\overrightarrow {AA'} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AC} = \overrightarrow c \). Chứng minh rằng \(\overrightarrow {B'C} = \overrightarrow c - \overrightarrow a - \overrightarrow b \) và \(\overrightarrow {BC'} = \overrightarrow a - \overrightarrow b + \overrightarrow c \)
Phương pháp giải - Xem chi tiết
Áp dụng quy tắc 3 điểm
Lời giải chi tiết
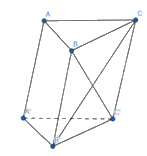
Ta có: \(\overrightarrow {B'C} = \overrightarrow {B'A'} + \overrightarrow {A'A} + \overrightarrow {AC} = - \overrightarrow {AB} - \overrightarrow {AA'} + \overrightarrow {AC} = - \overrightarrow a - \overrightarrow b + \overrightarrow c = \overrightarrow c - \overrightarrow a - \overrightarrow b \)
\(\overrightarrow {BC'} = \overrightarrow {BA} + \overrightarrow {AC} + \overrightarrow {CC'} = - \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AA'} = - \overrightarrow b + \overrightarrow c + \overrightarrow a = \overrightarrow a - \overrightarrow b + \overrightarrow c \)
Bài tập 5 trang 51 SGK Toán 12 tập 1 - Chân trời sáng tạo thuộc chương trình học về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn một bên, giới hạn tại một điểm và các tính chất của giới hạn để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập là vô cùng quan trọng để đạt kết quả tốt trong môn Toán.
Bài tập 5 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh tính giới hạn của hàm số tại một điểm cho trước. Các hàm số có thể là hàm đa thức, hàm hữu tỉ hoặc hàm lượng giác. Để giải quyết bài tập này, học sinh cần:
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài tập 5:
Để tính giới hạn của hàm số tại một điểm, ta có thể sử dụng phương pháp thay trực tiếp giá trị của điểm đó vào hàm số. Tuy nhiên, nếu kết quả là một dạng vô định, ta cần sử dụng các kỹ thuật biến đổi đại số để đơn giản hóa biểu thức trước khi tính giới hạn.
Ví dụ, nếu hàm số là f(x) = (x^2 - 1) / (x - 1), ta có thể phân tích tử số thành (x - 1)(x + 1) và rút gọn biểu thức thành f(x) = x + 1. Sau đó, ta có thể thay x = 1 vào hàm số để tính giới hạn.
Trong trường hợp hàm số có chứa căn thức, ta có thể sử dụng phương pháp nhân liên hợp để khử căn thức và đơn giản hóa biểu thức. Phương pháp này dựa trên việc nhân cả tử số và mẫu số với liên hợp của biểu thức chứa căn thức.
Đối với các hàm số lượng giác, ta có thể sử dụng các công thức lượng giác cơ bản để biến đổi biểu thức và tính giới hạn. Ví dụ, ta có thể sử dụng công thức sin^2(x) + cos^2(x) = 1 để đơn giản hóa biểu thức.
Ngoài bài tập 5, còn rất nhiều bài tập tương tự trong chương trình học về giới hạn của hàm số. Để giải quyết các bài tập này, học sinh cần nắm vững các kiến thức và kỹ năng sau:
Để củng cố kiến thức và kỹ năng giải bài tập về giới hạn của hàm số, học sinh nên luyện tập thêm với các bài tập khác trong SGK và các tài liệu tham khảo. Ngoài ra, học sinh cũng có thể tìm kiếm các bài giảng trực tuyến hoặc tham gia các khóa học luyện thi để được hướng dẫn chi tiết và giải đáp thắc mắc.
Bài tập 5 trang 51 SGK Toán 12 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính giới hạn của hàm số. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập là vô cùng quan trọng để đạt kết quả tốt trong môn Toán. Hy vọng rằng, với lời giải chi tiết và các hướng dẫn trong bài viết này, bạn sẽ tự tin hơn trong quá trình học tập và giải quyết các bài tập tương tự.